Sočasne značilnosti vektorjev, primeri in vaje

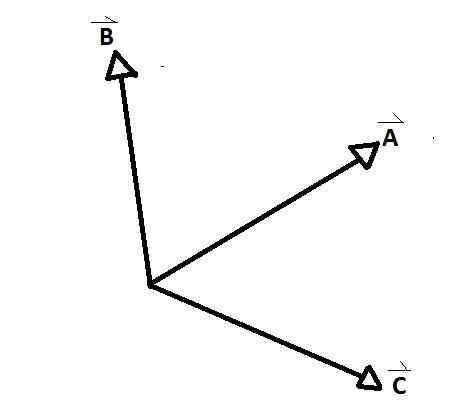
The sočasni vektorji So skupine vektorjev, katerih osi sovpadajo v enem trenutku in med vsakim parom tvorijo notranji in zunanji kot. Jasen primer opazimo na spodnji sliki, kjer so A, B in C sočasni vektorji.

D in E, za razliko od ostalih. Med sočasnimi vektorji AB, AC in CB so oblikovani koti. Kličejo se koti odnosov med vektorji.

[TOC]

Značilnosti

-Imajo skupno točko, ki sovpada z njihovim izvorom: vse velikosti sočasnih vektorjev se začnejo od skupne točke do svojih skrajnosti.

-Izvor se šteje za vektorsko akcijsko točko: vzpostaviti je treba točko ukrepanja, na katero bo neposredno vplival vsak sočasni vektorji.

-Vaša domena v ravnini in prostoru je R² in r³ oziroma: sočasni vektorji lahko pokrijejo celoten geometrijski prostor.

-Omogoča različne zapise v isti skupini vektorjev. Glede na študijske veje so v operacijah z vektorji prisotni različni zapisi.

Vrste vektorjev

Podružnica vektorjev ima več pododdelkov, med nekaterimi jih je mogoče imenovati: vzporedni, pravokotni, koplanarioji, ustrezni, nasprotni in enotni. Sočasni vektorji se pojavljajo na tem seznamu in tako kot vsi, ki so bili prej imenovani, imajo tudi v različnih znanostih veliko prijav.

V vektorski študiji so zelo pogosti, saj predstavljajo donosno posplošitev v operacijah z njimi. Tako v ravnini kot v vesolju so sočasni vektorji za trenutno uporabo za reprezentacijo različnih elementov in preučiti njihov vpliv na določen sistem.

Vektorska zapis

Obstajajo različni načini za predstavljanje vektorskega elementa. Glavna in najbolj znana sta:

Kartezijan

Predlaga ta isti matematični pristop, označuje vektorje s seznamom, ki ustreza velikosti vsake osi (x, y, z)

A: (1, 1, -1) Prostor A: (1, 1) Načrt

Polar

Služijo le za označevanje vektorjev v ravnini, čeprav je v integralnem izračunu dodeljena globina komponenta. Sestavljen je z linearno velikostjo r in kot glede na osi polarne osi Ɵ.

Vam lahko služi: inferencialna statistika: zgodovina, značilnosti, za kaj je, primeri

O: (3, 45⁰ ) Načrt A: (2, 45⁰ , 3) Prostor

Analitično

Določite veličine vektorja skozi verzorje. Versors (R&E + K) predstavljajo enotne vektorje, ki ustrezajo osi X, y in

A: 3i + 2J - 3K

Sferično

So podobni polarni zapisi, vendar z dodatkom drugega kota, ki pometa na ravnini Xy simbolizira δ.

O: (4, 60^tudi , π/4)

Operacije s sočasnimi vektorji

Sočasni vektorji se večinoma uporabljajo za opredelitev operacij med vektorji, saj je lažje primerjati elemente vektorjev, ko se pojavijo na hkrati.

Vsota (A + B)

Vsota sočasnih vektorjev želi najti nastali vektor V_r. Ki po mnenju veje študije ustreza končnemu ukrepanju

Na primer: 3 strune so vezane a, b, c do škatle, vsak konec vrvi je v rokah predmeta. Vsak od treh oseb mora vrv potegniti v smeri, ki ni druga 2.

A: (AX, AY, AZ) B: (BX, BY, BZ) C: (CX, CY, CZ)

A+b+c = (ax+bx+cx; ay+by+cy; az+bz+cz) = V_r

Škatla se lahko premakne samo v eno smer V_r bo označeval smer in občutek premika polja.

Razlika (a - b)

Obstaja veliko meril glede razlike med vektorji, mnogi avtorji se odločijo, da jo izključijo in trdijo, da je določena le vsota med vektorji, kjer je razlika vsota nasprotnega vektorja. Resnica je, da lahko algebraično vektorje odštejemo.

O: (sekira, ay, az) B: (bx, by, bz)

A-b = a + (-b) = (ax-bx; ay-be; az-bz) = [ax + (-bx); ay + (-by); az + (-bz)]

Skalarni izdelek (a . B

Znan tudi kot Punto Product, ustvari skalarno vrednost, ki je lahko povezana z več magnitudami v skladu z vejo študije.

Za geometrijo označuje območje paralelograma, ki ga tvori par sočasnih vektorjev z metodo paralelograma. Za mehansko fiziko določa delo, ki jo opravi sila F S premikanjem telesa na daljavo Δr.

Lahko vam služi: sestavljena sorazmernost: razlaga, tri sestavljene pravila, vaje

ѡ = f . Δr

Kot že ime pove, ustvari skalarno vrednost in je opredeljen na naslednji način:

Biti vektorji A in B

O: (sekira, ay, az) B: (bx, by, bz)

-Analitična oblika:

(Do . B) = | a |.| B |.Cos θ

Kjer je θ notranji kot med obema vektorji

-Algebrska oblika:

(Do . B) = (sekira.Bx + ay.z + az.Bz)

Vektorski izdelek (a x b)

Vektorski ali točkovni izdelek med dvema vektorjem definira tretji vektor C ki ima kakovost pravokotnega na B in C. V fiziki določa vektorski navor τ Osnovni element rotacijske dinamike.

-Analitična oblika:

| A x b | = | A |.| B |.Greh θ

-Algebrska oblika:

(A x b) = = (Sekira . by - ay . bx)- (sekira . BZ - AZ . bx) J + (Sekira . by - ay . bx) k

-Relativno gibanje: r_A/b

Osnova relativnosti je relativno gibanje in sočasni vektorji so osnova relativnega gibanja. Lahko sklepate po položajih, hitrostih in relativnih pospeškah z uporabo naslednjega vrstnega reda idej.

r _A/b = r_Do - r_B    ; Relativni položaj glede B

v _A/b = v_Do - v_B  ; Relativna hitrost spoštovanja do B

do _A/b = a_Do - do_B  ; Relativni pospešek spoštovanja do B

Primeri: rešene vaje

Vaja 1

Naj A, B in C sočasni vektorji.

A = (-1, 3, 5) b = (3, 5, -2) c = (-4, -2, 1)

-Določite nastali vektor V_r = 2a - 3b + c

2a = (2 (-1), 2 (3), 2 (5)) = (-2, 6, 10)

-3B = (-3 (3), -3 (5), -3 (-2)) = (-9, -15, 6)

V_r = 2a + (-3b) + c = (-2, 6, 10) + (-9, -15, 6) + (-4, -2, 1)

V_r = (-2+(-9)+(-4)]; [6+(-15)+(-2)]; (10+6+1))

V_r = (-15, -11, 17)

-Določite skalarni izdelek (a . C)

(Do . C) = (-1, 3, 5) . (-4, -2, 1) = (-1) (-4) + 3 (-2) + 5 (1) = 4 -6 + 5

(Do . C) = 3

-Izračunajte kot med A in C

(Do . C) = | a |.| C |.Cos θ, kjer je θ najkrajši kot med vektorji

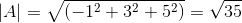
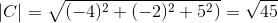
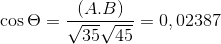
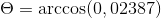
θ = 88.63⁰

 -Poiščite vektor, pravokoten na A in B

Za to je treba določiti vektorski izdelek med (-1, 3, 5) in (3, 5, -2). Kot je bilo razloženo prej, je zgrajena matrica 3 x 3, kjer je prva vrstica sestavljena iz seznama enot vektorjev (i, j, k). Potem je 2. in 3. vrstica sestavljena iz vektorjev, ki jih je treba upravljati, ob upoštevanju operativnega naročila.

Vam lahko služi: decimalni zapis

(A x b) = [(-1) . 5 - (3 . 3)] Yo  - [(-1) . (-2) - (5 . 3)] J + [(-1) . 5 - (3 . 3)] k

(A x b) = (-5 - 9) Yo - (2 - 15) J + (-5 - 9) k         

(A x b) =  -14 i + 13 j - 14 k

Vaja 2 

Naj v_do in v_b Vektorji hitrosti A in B. Izračunajte hitrost B iz a.

V_do = (3, -1, 5) v_b = (2, 5, -3)

V tem primeru se zahteva relativna hitrost B V_B/a

V_B/a = V_B - V_Do

V_B/a = (2, 5, -3) -(3, -1, 5) = (-1, 6, -8)

To je veloc vektor B, ki ga vidimo iz. Kjer je nov vektor hitrosti B opisan s sklicevanjem opazovalca, nameščenega v A in se premika s hitrostjo a.

Predlagane vaje

1-konstrukcija 3 vektorjev A, B in C, ki so sočasno in povezujejo 3 operacije med njimi s praktično vajo.

2 -Vektorji A: (-2, 4, -11), b: (1, -6, 9) in c: (-2, -1, 10). Poiščite pravokotne vektorje do: A in B, C in B, vsota A + B + C.

4-determin 3 vektorji, ki so med seboj pravokotni, ne da bi upoštevali koordinatne osi.

5 definirajte delo, ki jo opravi sila, ki dvigne 5 kg bloka mase, od dna 20 m globoke vrtine.

6-SWAMKER ALGEBRIC, da je odštevanje vektorjev enako vsoti nasprotnega vektorja. Upravičite svoje postulate.

7-denote Vektor v vseh zapisih, razvitih v tem članku. (Kartezijanska, polarna, analitika in sferična).

8-Magnetne sile, ki se izvajajo na magnetu, ki počiva na mizi, dajejo naslednji vektorji; V: (5, 3, -2), t: (4, 7, 9), h: (-3, 5, -4). Določite, v katero smer se bo magnet premikal, če bodo hkrati delovale vse magnetne sile.

Reference

1. Evklidska geometrija in preobrazbe. Clayton w. umakniti. Couer Corporation, 1. januar. 2004
2. Kako rešiti težave z matematiko l. Moiseiwitsch. Couer Corporation, 10. april. 2013
3. Osnovni koncepti geometrije. Walter Prenowz, Meyer Jordan. Rowman & Littlefield, 4. oktober. 2012
4. Vektorji. Rocío Navarro Lacoba, 7. junij. 2014
5. Linearna algebra. Bernard Kolman, David R. Hrib. Pearson Education, 2006