Kolinealni vektorji

Pojasnjujemo, kaj so kolinealni vektorji, sistem Colineal Vectors in damo več primerov

Kateri so collinealni vektorji?

The Kolinealni vektorji So ena od treh vrst obstoječih vektorjev. To so tisti vektorji, ki so v isti smeri ali linijo ukrepanja. To pomeni naslednje: Dva ali več vektorjev bosta kolinealna, če obstaja primer, da sta razporejena v linijah, ki so vzporedni med seboj.

Vektor je opredeljen kot velikost, ki se uporablja za telo in je značilna, da ima smer, občutek in lestvico. Vektorji najdemo v ravnini ali v prostoru in so lahko različnih vrst: kolinealni vektorji, sočasni vektorji in vzporedni vektorji.

Kdaj so kolinealni vektorji?

Vektorji so kolinealni, če je linija delovanja ene popolnoma enaka delovanju vseh drugih vektorjev, ne glede na velikost in smer vsakega od vektorjev.

Vektorji se uporabljajo kot reprezentacije na različnih področjih, kot so matematika, fizika, algebra in tudi v geometriji, kjer so vektorji samo, kadar je njihova smer enaka, ne glede na to, da njihov pomen ni.

Primeri kolinealnih vektorjev

• Dva ali več vektorjev je kolinealna, če je razmerje med koordinatami enako.

Primer 1

Imate vektorje m = m_x; m_y in n = n_x; N_. To so kolinearne, če:

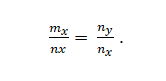
Primer 2

Lahko ga določimo, če sta vektorji j = 3,6,15 in p = 1,2,5 kolinearna skozi razmerje med njihovimi koordinatami, ki jih morate biti sorazmerni med seboj; to pomeni: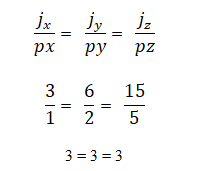

• Dva ali več vektorjev je kolinealna, če je razmnoževanje izdelka ali vektorja enako nič (0). To je zato, ker je v koordinatnem sistemu značilno vsakega vektorja njihove koordinate, in če so med seboj sorazmerne, bodo vektorji kolinearni. To je izraženo na naslednji način:

Vam lahko služi: enakovredni sklopi: kaj so, razlaga, primeri

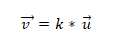
Primer 1

Imate vektorje A = (10, 5) in B = (6, 3). Za ugotovitev, ali so kolinealne, se uporablja določilna teorija, ki vzpostavlja enakost navzkrižnih produktov. Na ta način morate:

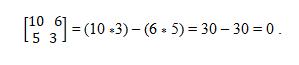
Kolinealni vektorski sistem

Kolinealni vektorji so grafično predstavljeni s smerjo in smerjo teh - če upoštevamo, da morajo iti skozi točko uporabe - in modula, ki je določena lestvica ali dolžina.

Kolinealni vektorski sistem se oblikuje, ko dva ali več vektorjev delujeta na predmet ali telo, ki predstavljajo silo in delujejo v isto smer.

Na primer, če se na telo naneseta dve kolinealni sili, bo posledica tega, da je ena od teh odvisna le od občutka, v katerem delujejo. Obstajajo trije primeri, ki so:

Kolinealni vektorji z nasprotnimi čutili

Rezultat dveh kolinealnih vektorjev je enak vsoti teh:

R = ∑ f = f₁ + F_2.

Primer

Če dve F sili delujeta na vozičku₁ = 40 N in F₂ = 20 N v nasprotni smeri (kot je prikazano na sliki), je rezultat:

R = ∑ f = (- 40 n) + 20n.

R = - 20 n.

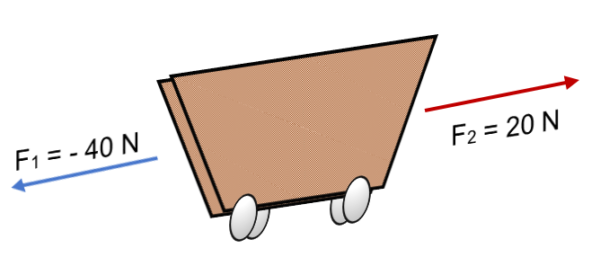Negativni znak izraža, da se bo telo premaknilo na levo, s silo, enakovredno 20 N.

Kolinealni vektorji v istem smislu

Obseg nastale sile bo enaka vsoti kolonialnih vektorjev:

R = ∑ f = f₁ + F_2.

Primer

Če dve F sili delujeta na vozičku₁ = 35 N in F₂ = 55 N v isti smeri (kot je prikazano na sliki), rezultat je:

R = ∑ f = 35 n + 55n.

R = 90 n.

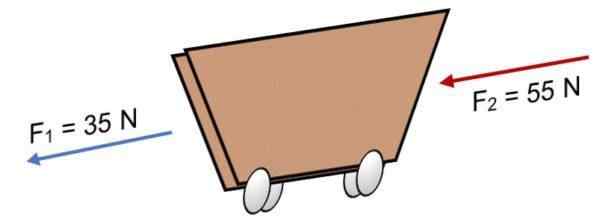
Pozitiven rezultat kaže, da kolinealni vektorji delujejo na levi strani.

Lahko vam služi: pravilo T: značilnosti, tako da so primeri

Kolinealni vektorji z enakimi velikostmi in nasprotnimi čutili

Rezultat obeh kolinealnih vektorjev bo enak vsoti kolinearnih vektorjev:

R = ∑ f = f₁ + F_2.

Ker imajo sile enako velikost, vendar v nasprotni smeri -to je, da bo ena pozitivna in druga negativna -z dodajanjem obeh sil bo rezultat enak nič.

Primer

Če dve F sili delujeta na vozičku₁ = -7 n in f₂ = 7 N, ki imajo enako velikost, vendar v nasprotni smeri (kot je prikazano na sliki), je rezultat:

R = ∑ f = (-7 n) + 7n.

R = 0.

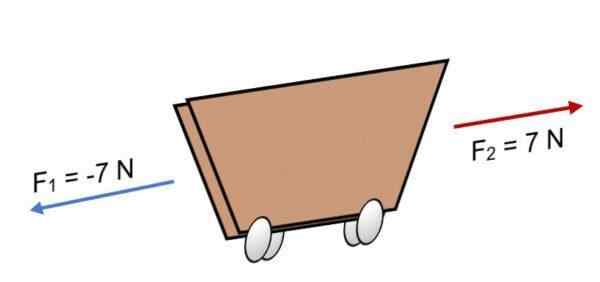
Kot rezultat je enak 0, pomeni, da se vektorji medsebojno uravnotežijo in zato je telo v ravnovesju ali počitku (ne bo premikalo se).

Razlika med kolinealnimi in sočasnimi vektorji

Za kolinealne vektorje je značilno, da imajo isto smer na isti črti ali ker so vzporedni s črto; To pomeni, da gre za vzporedne režiserje linij.

Sočasni vektorji so opredeljeni, ker so v različnih poteh delovanja, ki se prestrežejo v eni točki.

Z drugimi besedami, imajo enako točko izvora ali prihoda -ne glede na njihov modul, pomen ali smeri -oblikovanje kota med njimi.

Sočasni vektorski sistemi se razrešijo z matematičnimi ali grafičnimi metodami, ki so paralelogramska metoda sil in metoda sil poligona. Skozi te bo določena vrednost nastalega vektorja, kar kaže na smer, v katero se bo telo premikalo.

V bistvu je glavna razlika med kolinearnimi in sočasnimi vektorji v akciji, v kateri delujejo: Collineals delujejo v isti vrstici, medtem ko sočasni v različnih.

Vam lahko služi: sistem enačb: metode rešitve, primeri, vaje

To pomeni, da kolinearni vektorji delujejo v eni ravnini, "x" ali "y"; In sočasno dejanje v obeh ravninah, začenši z iste točke.

Kolinealni vektorji niso v enem trenutku, kot to počnejo sočasni, ker so vzporedni med seboj.

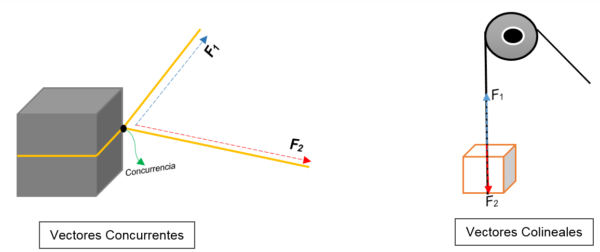
Na levi sliki lahko vidite blok. Vezana je z vrvjo in vozel jo deli na dva; Ko ga najdemo proti različnim usmeritvam in z različnimi silami, se bo blok premaknil v isto smer.

V eni točki sta predstavljena dva vektorja (blok), ne glede na njihov modul, smer ali smer.

Po drugi strani se na pravi sliki pojavi jermenica, ki dvigne škatlo. Vrv predstavlja linijo delovanja; Ko se ustavi, nanjo delujeta dve sili (vektorji): napetostna sila (pri plezanju v blok) in druge sile, ki izvaja težo bloka. Oba imata isto smer, vendar v nasprotnih čutilih; Nekoč se ne strinjajo.