Fizično

Vektorska direktorica enačbe linije, rešene vaje

Vektorska direktorica enačbe linije, rešene vaje

Razume ga Direktor Vector Tisti, ki definira smer črte, bodisi v ravnini bodisi v vesolju. Zato lahko vektor, vzporeden s črto.

To je mogoče zahvaljujoč aksiomu evklidske geometrije, ki pravi, da dve točki določata črto. Nato orientirani segment, ki tvorita ta dve točki, določa tudi vektorskega direktorja te vrstice.

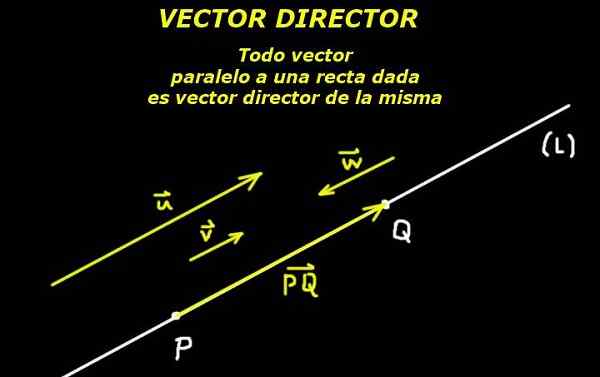Slika 1. Vektorski direktor linije. (Lastna izdelava)

Glede na točko Str pripada vrsti (L) in glede na režiserskega vektorja ali Od te vrstice je črta popolnoma določena.

[TOC]

Enačba linije in režiserja

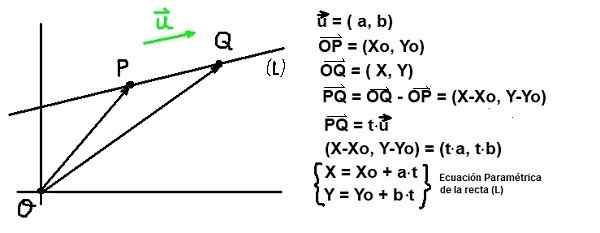
Slika 2. Enačba linije in režiserja. (Lastna izdelava)

Glede na točko Str koordinat V: (xo, jaz) in vektor ali Direktor linije (L), Vse točke Q koordinat V: (x, y) mora izpolniti to vektor Pq biti vzporedni z u. Ta zadnji pogoj je zagotovljen, če Pq Je sorazmerno ali:

Pq = T⋅ali

V prejšnjem izrazu t To je parameter, ki spada v resnične številke.

Če kartezijanske komponente Pq in od ali Prejšnja enačba je napisana na naslednji način:

(X-xo, y-yo) = t⋅ (a, b)

Če so komponente vektorske enakosti enake naslednjim par enačb:

X - xo = a⋅t      in   In - jaz = b⋅t 

Parametrična enačba vrstice

Koordinate X in In točke, ki pripada črti (L) ki gre skozi koordinatno točko (Xo, jaz) In je vzporedno z Direktor Vector ali= (a, b) Določijo jih z dodeljevanjem resničnih vrednosti spremenljivemu parametru t:

X = xo + a⋅t; Y = jaz + b⋅t

Primer 1

Za ponazoritev pomena parametrične enačbe vrstice jemljemo kot režiser

Vam lahko služi: valovita optika

ali = (a, b) = (2, -1) 

in kot znana točka črte 

P = (xo, jaz) = (1, 5). 

Parametrična enačba vrstice je:

X = 1 + 2⋅t; Y = 5 - 1⋅t; -∞

Za ponazoritev pomena te enačbe Slika 3 prikazuje, kjer parameter T spreminja vrednost in točko Q  koordinat (X, y) Zavzemite različne položaje na črti.

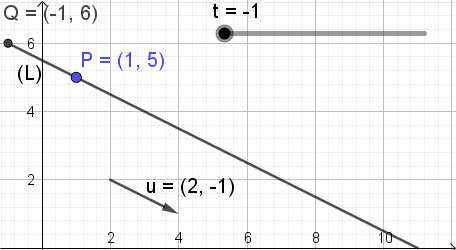Slika 3. Pq = t u. (Lastna izdelava)

Črta v vektorski obliki

Glede na točko P linije in njegovega direktorja ali enačba vrstice lahko zapišemo v vektorski obliki:

OQ = Op + λ⋅ali 

V prejšnji enačbi, ki je vsaka točka, vendar pripada vrstici in λ Resnična številka.

Vektorska enačba vrstice je uporabna za poljubno število dimenzij, definirati je mogoče celo hiper -eret.

V tridimenzionalnem primeru za direktorja vektorja ali= (a, b, c) in točka P = (xo, jaz, zo), Koordinate generične točke Q = (x, y, z) Pripadnost črti je:

(X in z) = (Xo, i, zo) + λ⋅ (a, b, c)

Primer 2

Ponovno razmislite o vrstici, ki je kot direktor režiserja  

ali = (a, b) = (2, -1) 

in kot znana točka črte 

P = (xo, jaz) = (1, 5). 

Vektorska enačba te vrstice je:

(X, y) = (1, 5) + λ⋅ (2, -1) 

Neprekinjena oblika linije in režiserski vektor

Začenši iz parametrične oblike, čiščenje in ujemanje parametra λ imate:

(X-xo)/a = (y-yo)/b = (z-zo)/c

To je simetrična oblika enačbe črte. čutim da do, b in c So sestavni deli režiserskega vektorja.

Primer 3

Razmislite o vrsti, ki je kot direktor direktorja  

ali = (a, b) = (2, -1) 

in kot znana točka črte 

Vam lahko služi: kakšna je elektrika? (S poskusom)

P = (xo, jaz) = (1, 5). Poiščite njegovo simetrično obliko.

Simetrična ali neprekinjena oblika je črta::

(X - 1)/2 = (y - 5)/( - 1)

Splošna oblika enačbe črte

Znana je kot splošna oblika črte v ravnini xy do enačbe, ki jo ima naslednja struktura:

A⋅x + b⋅y = c

Izraz simetrične oblike je mogoče napisati tako, da ima splošno obliko:

B⋅x - a⋅y = b⋅xo - a⋅O

Primerjava s splošno obliko vrstice ostaja: 

A = b, b = -a in c = B⋅XO - A⋅O 

Primer 3

Poiščite splošno obliko vrstice, katere režiser je u = (2, -1)

 In kaj gre skozi točko P = (1, 5).

Za iskanje splošne oblike lahko uporabimo dane formule, vendar bo izbrana alternativna pot.

Začnemo z iskanjem dvojnega vektorja U vektorja, ki je opredeljen kot vektor, ki ga dobimo z izmenjavo komponent U, in pomnoževanjem za -1 drugega:

W= (-1, -2)

Dvojni vektor W ustreza vrtenju v 90 ° v razporedu direktorja direktorja v.

Pomnožimo plezanje W z (X, y) in z (Xo, jaz) In se ujemamo:

(-1, -2) • (x, y) = (-1, -2) • (1, 5)

-X -2y = -1 -2⋅5 = -11

Končno ostane:

X + 2y = 11

Standardna oblika enačbe črte

Znana je kot standardna oblika črte v ravnini XY, tista, ki ima naslednjo strukturo:

Y = m⋅x + d

kjer m predstavlja prestrezanje naklona in D z osi in.

Glede na režiser u = (a, b) vektor, je naklon m b/a.

In D dobimo z zamenjavo X in Y z znano točko XO, ME:

I = (b/a) xo + d.

Skratka, m = b/a y d = me -(b/a) xo

Upoštevajte, da je naklon M količnik med komponento in režiserja in komponente x istega.

Vam lahko služi: rotacijsko ravnovesje: formule in enačbe, primeri, vaje

Primer 4

Poiščite standardno obliko vrstice, katere režiser je u = (2, -1) 

In kaj gre skozi točko P = (1, 5).

M = -½ in d = 5 -( -½) 1 = 11/2

Y = (-1/2) x + 11/2

Rešene vaje

-Vaja 1

Poiščite vektorskega direktorja črte (L), ki je presečišče ravnine (π): x - y + z = 3 in ravnina (ω): 2x + y = 1.

Nato napišite neprekinjeno obliko vrstice vrstice (l).

Rešitev

Iz ravninske enačbe (ω) Očistek y: y = 1 -2x

Nato nadomestimo v ravninski enačbi (π):

X - (1 - 2x) + z = 3 ⇒ 3x + z = 4 ⇒ z = 4 - 3x

Nato parametriziramo x, izberemo parametrizacijo x = λ

To pomeni, da ima črta vektorsko enačbo, ki jo daje:

(X, y, z) = (λ, 1 - 2λ, 4 - 3λ)

ki je mogoče napisati kot:

(X, y, z) = (0, 1, 4) + λ (1, -2, -3)

S tem, kar je jasno, da vektor ali = (1, -2, -3) je naravnost upravljanje vektorja (l).

Neprekinjena oblika črte (l) je:

(X - 0)/1 = (y - 1)/( - 2) = (z - 4)/( - 3)

-Vaja 2

Glede na 5x ravnino + do Y + 4z = 5 

in črta, katere enačba je x/1 = (y-2)/3 = (z -2)/(-2)

Določite vrednost do tako da sta ravnina in črta vzporedna.

Rešitev 2

Vektor n = (5, a, 4) je normalen vektor do letala.

Vektor ali = (1, 3, -2) je naravni upravitelj.

Če je črta vzporedna z ravnino, potem n • v = 0.

(5, do, 4)•(1, 3, -2) = 5 +3do -8 = 0 ⇒ do= 1.

Reference

  1. Fleming, w., & Varberg, D. In. (1989). Prealculus matematika. Prentice Hall Ptr.
  2. Kolman, b. (2006). Linearna algebra. Pearson Education.
  3. Zvest, J. M., & Viloria, n. G. (2005). Ravna analitična geometrija. Mérida - Venezuela: Venezuelska uredništvo c. Do.
  4. Navarro, Rocio. Vektorji. Obnovi se od: Knjige.Google.co.pojdi.
  5. Pérez, c. D. (2006). Prequalculus. Pearson Education.
  6. Prenowitz, w. 2012. Osnovni koncepti geometrije. Rowman & Littlefield.
  7. Sullivan, m. (1997). Prequalculus. Pearson Education.