Nenehne spremenljive značilnosti, primeri in vaje

The Neprekinjena spremenljivka To je ena, ki lahko vzame neskončno število številčnih vrednosti med dvema danima vrednostma, tudi če sta ti dve vrednosti poljubno zaprti. Uporabljajo se za opis merljivih atributov; na primer višina in teža. Vrednosti, ki jih vzame neprekinjena spremenljivka, so lahko racionalne številke, realne ali zapletene številke, čeprav je ta zadnji primer v statistiki manj pogost. 

Glavna značilnost neprekinjenih spremenljivk je, da je med dvema racionalnima ali resničnimi vrednostmi vedno mogoče najti, med drugim in prvim pa lahko najde drugo vrednost in tako v nedogled.

Slika 1. Krivulja predstavlja neprekinjeno porazdelitev in palice diskretno. Vir: Pixabay

Recimo na primer teže v skupini, kjer ima največja teža 95 kg in najnižjo težo 48 kg; To bi bil obseg spremenljivke in število možnih vrednosti je neskončno.

Na primer med 50,00 kg in 50,10 kg je lahko 50,01. Toda med 50,00 in 50,01 je lahko ukrep 50,005. To je neprekinjena spremenljivka. Po drugi strani pa bi bila določena ena decimalna natančnost, če je v možnih ukrepih, potem bi bila uporabljena spremenljivka diskretna.

Neprekinjene spremenljivke spadajo v kategorijo kvantitativnih spremenljivk, ker imajo povezano številčno vrednost. S to numerično vrednostjo je mogoče izvajati matematične operacije, ki segajo od aritmetike do metod neskončnega izračuna. 

[TOC]

Primeri

Večina spremenljivk fizike je neprekinjenih spremenljivk, med njimi lahko poimenujemo: dolžina, čas, hitrost, pospešek, energija, temperatura in druge.

Neprekinjene spremenljivke in diskretne spremenljivke

V statističnih podatkih je mogoče opredeliti različne vrste spremenljivk, tako kvalitativno kot kvantitativno. Neprekinjene spremenljivke pripadajo tej zadnji kategoriji. Z njimi je mogoče izvajati aritmetične in izračunske operacije.

Na primer spremenljivka h, ustreza ljudem z višino med 1,50 m in 1,95 m, je neprekinjena spremenljivka. 

Primerjajmo to spremenljivko s to drugo: tolikokrat, ki je draga pri zagonu valute, ki jo bomo poklicali n.

Spremenljivka n Lahko pa vzamete vrednosti med 0 in neskončnostjo n To ni neprekinjena spremenljivka, saj ne more sprejeti vrednosti 1.3 ali 1,5, ker med vrednostmi 1 in 2 ni drugega. To je primer Diskretna spremenljivka.

Izvajanje neprekinjenih spremenljivk

Razmislite o naslednjem primeru: stroj proizvaja tekme fosforja in jih spakira v svojo škatlo. Določeni sta dve statistični spremenljivki:

Vam lahko služi: izobarični postopek: formule, enačbe, poskusi, vaje

Spremenljivka 1: l = dolžina plaze.

Spremenljivka 2: n = število prašičev na polje.

Dolžina nominalnih ujemanja je 5,0 cm z 0,1 cm toleranco. Število prašičev na škatlo je 50 s toleranco 3.

a) navedite obseg vrednosti, ki lahko vzamejo L in N.

b) Koliko vrednosti lahko vzamete L?

c) Koliko vrednosti lahko vzamete n?

Recimo v vsakem primeru, če gre za diskretno ali neprekinjeno spremenljivko.

Rešitev

Vrednosti L Razumejo jih v intervalu [5,0-0,1; 5,0+0,1]; to pomeni, da vrednost L je v intervalu [4,9 cm; 5.1 cm] in spremenljivka L Med tema dvema ukrepoma lahko vzamete neskončne vrednosti. Nato je neprekinjena spremenljivka.

Vrednost spremenljivke n je v intervalu [47; 53]. Spremenljivka n V intervalu tolerance lahko vzame le 6 možnih vrednosti, potem je diskretna spremenljivka.

Vaja Porazdelitev verjetnosti

Če so vrednosti spremenljivke poleg neprekinjene, so povezane z določeno verjetnostjo pojavljanja, potem je to a Neprekinjena naključna spremenljivka. Zelo pomembno je razlikovati, ali je spremenljivka diskretna ali neprekinjena, saj so verjetnostni modeli, ki veljajo za drug drugega.

Neprekinjena naključna spremenljivka je popolnoma opredeljena, kadar so znane vrednosti, ki jih lahko prevzamejo, in verjetnost, da se mora vsak od njih zgoditi.

-Vaja 1 verjetnosti

Tovarna tekma jih naredi tako, da je dolžina palic vedno med 4,9 cm in 5,1 cm in nič od teh vrednosti. Obstaja verjetnost, da dobimo palico, ki meri med 5,00 in 5,05 cm, čeprav bi lahko izvlekli tudi eno od 5.0003 cm. So te vrednosti enako verjetne?.

Vam lahko služi: relativna gostota: izračun, primeri, vaje

Rešitev

Recimo, da je gostota verjetnosti enakomerna. Nato so navedene možnosti za iskanje fosforja z določeno dolžino:

-Da je fosfor v območju [4,9; 5,1] ima verjetnost = 1 (ali 100%), saj stroj ne ujema iz teh vrednosti.

-Iskanje fosforja, ki je med 4,9 in 5,0, ima verjetnost = ½ = 0,5 (50%), saj je polovica razpona dolžin.

-In verjetnost, da ima tekma dolžino med 5,0 in 5,1, je tudi 0,5 (50%)

-Znano je, da ni fosforjevih palic, ki bi imele dolžino med 5,0 in 5,2. Verjetnost: nič (0%).

Verjetnost iskanja palice v določenem območju

Zdaj pa opazujmo naslednje verjetnosti p, da dobimo palice, katerih dolžina je med l₁ in l₂:

 P = (l₂ -l₁) /(L_Max - L_min)

-P, da ima tekma dolžino med 5,00 in 5,05 P ([5.00; 5.05]):

P ([5,00; 5,05]) = (5,05 - 5,00)/(5,1 - 4,9) = 0,05/0,2 = ¼ = 0,25 (25%)

-P, da ima Cerrillo dolžino med 5,00 in 5,01, je:

P ([5.00; 5,01]) = (5,00 - 5,01)/(5,1 - 4,9) = 0,01/0,2 = 1/20 = 0,05 (5 %)

-P, da ima Cerrillo dolžino med 5.000 in 5.001, je še nižje:

P (5.000; 5,001) = 0,001/0,2 = 1/200 = 0,005 (0,5%)

Če še naprej zmanjšujemo interval, da se vedno bolj približamo do 5,00, verjetnost, da ima palica točno 5,00 cm, je nič (0%). Kar imamo, je verjetnost, da bomo našli tekmo v določenem območju.

Verjetnost, da bi v določenem območju našli več palic

Če so dogodki neodvisni, je verjetnost, da sta dve palici v določenem območju, produkt njihovih verjetnosti.

-Verjetnost, da sta dve palici med 5,0 in 5,1, je 0,5*0,5 = 0,25 (0,25%)

-Verjetnost, da je 50 palic med 5,0 in 5,1, je (0,5)^50 = 9 × 10^-16, to je skoraj nič.

-Verjetnost, da je 50 palic med 4,9 in 5,1, je (1)^50 = 1 (100%)

-Vaja 2 verjetnosti

V prejšnjem primeru je bila podana predpostavka, da je verjetnost v danem intervalu enakomerna, vendar ni vedno tako.

Vam lahko služi: hidrostatični tlak: formula, izračun, primeri, vaje

V primeru pravega stroja, ki proizvaja palice, je možnost, da je palica v osrednji vrednosti, večja kot v eni od ekstremnih vrednosti. Z matematičnega vidika je to modelirano s funkcijo f (x), znano kot gostota verjetnosti.

Verjetnost, da je ukrep med A in B, izračuna z določenim integralom funkcije F (x) med A in B. 

Kot primer, predpostavimo, da želimo najti funkcijo f (x), ki predstavlja enakomerno porazdelitev med vrednostmi 4.9 in 5.1 vaje 1. 

Če je porazdelitev verjetnosti enakomerna, potem je F (x) enak konstantni C, ki je določena, da integral med 4,9 in 5,1 C. Ker je ta integral verjetnost, mora biti rezultat 1.

Slika 2. Enotna gostota verjetnosti. (Lastna izdelava)

Kar pomeni, da je C vreden 1/0,2 = 5. Z drugimi besedami, funkcija enakomerne gostote verjetnosti je f (x) = 5, če 4,9≤x≤5,1 in 0 iz tega območja. Slika 2 prikazuje enotno funkcijo gostote verjetnosti.

Opomba kot v presledkih iste širine (na primer 0,02) je verjetnost enaka v središču kot na koncu kontinuiranega spremenljivega območja L (Dolžina kumaric).

Bolj realističen model bi bila verjetnost gostote kot naslednja:

-f (x) = -750 ((x-5.0)^2-0.01) Če 4,9≤x≤5,1

-0 zunaj tega območja 

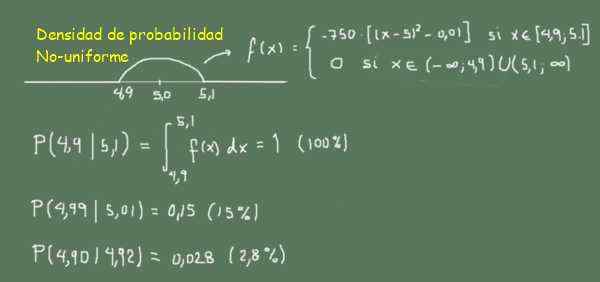Slika 3. Funkcija gostote verjetnosti verjetnosti. (Lastna izdelava)

Na sliki 3 ga lahko opazimo, saj je verjetnost, da najdete palice med 4,99 in 5,01 (širina 0,02), večja od iskanja palic med 4,90 in 4,92 (širina 0,02)

Reference

1. Dinov, IVO. Diskretne naključne spremenljivke in porazdelitve verjetnosti. Obnovljeno od: stat.UCLA.Edu
2. Diskretne in neprekinjene naključne spremenljivke. Okreval od: OCW.MIT.Edu
3. Diskretne naključne spremenljivke in porazdelitve verjetnosti. Okrevano od: domača stran.Ddms.Uiowa.Edu
4. H. Peshro. Uvod v verjetnost. Obnovi se od: verjetnostnega tečaja.com
5. Mendenhall, w. 1978. Statistični podatki za upravo in ekonomijo. Ibero -ameriška uredniška skupina. 103-106.
6. Naključne spremenljive težave in verjetnostni modeli. Okreval od: ugr.je.
7. Wikipedija. Neprekinjena spremenljivka. Okreval iz Wikipedije.com
8. Wikipedija. Statistična spremenljivka. Okreval iz Wikipedije.com.