Značilnosti poševni trikotniki, primeri, vaje

The Poševni trikotniki So tisti, ki nimajo pravega kota, zato noben njihov notranji koti ni enak 90 °. Torej, poševni trikotnik je lahko Akutant ali obtuse.

V prvem primeru so notranji koti trikotnika akutni ali kaj je enako: manj kot 90 °, v drugem. Poglejmo primer vsakega na naslednji sliki:

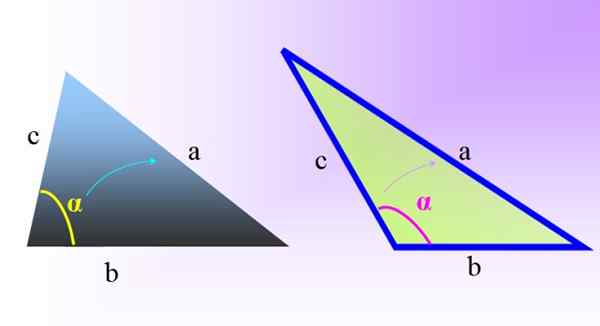Slika 1. Poševni trikotniki: na levi poševni in akutantni trikotnik. Na desni poševni in obtuje. Vir: f. Zapata.

Če želite najti dolžine strani in ukrepov notranjih kotov tovrstnih trikotnikov.

Vendar pa obstajajo alternative za reševanje trikotnika: teoreme kosinusa in naročja ter dejstvo, da je vsota notranjih kotov enaka 180 °.

[TOC]

Primeri Triangles Oblicuágulos

Če se bomo usmerili po sliki 1.

Akutantni trikotnik

Biti trikotnik strani A, B in C, z α kot pred stranjo.

Če je kvadrat na strani nasproti akutnemu kotu α, je manjši od vsote kvadratov preostalih strani. Algebraično:

do² < b² + c²; α < 90º

Relativni enakostranični trikotnik, tisti, ki ima tri strani istega ukrepa.

OBTUSE TRIKANJE

Po drugi strani pa, če je kvadrat na nasprotni strani do Pod kotom je α večji od vsote kvadratov drugih dveh. Zato:

do² > b² + c²; α> 90 °

Na primer, trikotnik, katerega notranji koti so 105 °, 60 ° in 15 °, je obljubljen poševni trikotnik. Upoštevajte, da je 105 ° + 60 ° + 15 ° = 180 °.

Teoreme sinusa in kosinusa

Za reševanje poševnih trikotnikov, to je, da bi našli ukrepe vseh strani in vseh njihovih zornih kotov, so potrebni teoremi dojk in kosinusa.

Naj bo A, B in C strani trikotnika ter α, β in γ njihove notranje kote. Tako:

Teorem dojk

Teorem dojk vzpostavi naslednje:

Kjer je α nasprotni kot do strani A, je β kot, ki nasprotuje strani B in γ, kot pred stran C.

Lahko vam služi: antiderivativ: formule in enačbe, primeri, vaje

Enakovreden:

Ko bomo rešili trikotnik, se odločimo uporabiti teorem o dojki, kot je znanih več kotov kot strani.

Teorem Coseno

Glede na teorem Coseno:

c² = a² + b² - 2⋅A⋅B⋅cos γ

Spet je kot γ pred stranjo c. Prav tako lahko napišemo enakovredne izraze za strani A in B, kot sledi:

do² = b² + c² - 2⋅B⋅C⋅COS α

In

b² = a² + c² - 2⋅A⋅c⋅cos β

Kosinusni teorem se uporablja po možnosti, kadar je znana vrednost dveh strani in kota med njima. Tudi ko so znane tri strani trikotnika, nam teorem omogoča izračun kosinusa kota med dvema od njih.

Rešene vaje

- Vaja 1

Preverite, ali je trikotnik, katerega strani merijo 20, 10 in 12 poljubnih enot.

Rešitev

Ne poznamo nobenega od notranjih zornih kotov, toda glede na merila, ki služijo prepoznavanju osupljivih trikotnikov.

Najprej najdemo kvadratke na vsaki strani:

dvajset² = 400

10² = 100

12² = 144

In to vidimo res: 400> 100 + 144, saj 400> 244. Zato trikotnik vsebuje kot, večji od 90 °, ki se nahaja pred stranjo, ki meri 20. Posledično je ta trikotnik poleg poševnega tudi nejasnega.

- Vaja 2

Glede na poševni trikotnik, prikazan na sliki 2, katerega ukrepi so podani v poljubnih enotah, določite:

a) Vrednost x. Ali gre za akutantni ali obtuse?

b) preostali notranji koti trikotnika

c) obod

d) Območje.

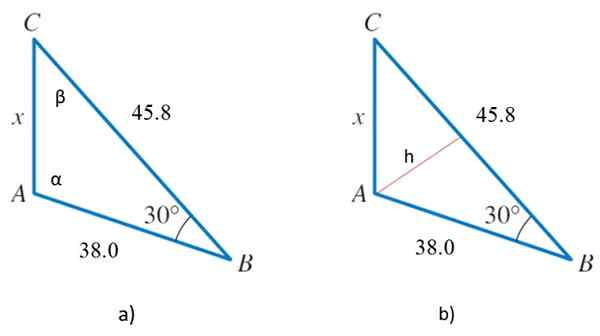Slika 2. 2a) Trikotnik za leto razreši 2 in 2b) isti trikotnik z višino, ki bo služil za določitev območja. Vir: f. Zapata.

Rešitev

Od trikotnika sta znani dve sosednji strani, katerih ukrepi so 38.0 in 45.8 in kot med njimi, ki je 30 °, zato se takoj uporabi kosinusni teorem:

x² = 38.0² + Štiri. Pet.8² - 2 x 38.0 x 45.8 x cos 30 ° = 527.18

Zato:

x = (527.18^1/2 = 22.96

Risba kaže, da je α> 90 ° in trikotnik poleg poševnega poleg poševnih. Če želite preveriti, najdemo kvadratke strani, kot je bilo to storjeno v prejšnji vaji:

22.96² = 527.18

38.0² = 1444.00

Štiri. Pet.8² = 2097.64

Kot α je večji od 90 °, če je res od kvadrata nasprotne strani: 45.8²  Je večja od vsote kvadratov drugih strani, ki je 22.96² + 38.0².

Vam lahko služi: zakoni eksponentov

Poglejmo, če se to zgodi:

527.18 + 1444.00 = 1971.2

Prav zares:

2097.64> 1971.2

Zato je kot α večji od 90 °.

Rešitev b

Zdaj lahko uporabimo teorem o dojki, da najdemo enega od manjkajočih zornih kotov. Dvignili ga bomo za kota β:

Sen 30 ° / 22.96 = sin β / 38

Sen β = 38 x (Sen 30º / 22.96) = 0.8275

β = arcsen (0.8275) = 55.84 °

Manjkajoč kot je mogoče najti, vedoč, da je vsota notranjega kota katerega koli trikotnika 180 °. Zato:

55.84º + 30 ° + α = 180 °

α = 94.16 °

Če je prednostno, lahko uporabite tudi kosinus. Ko se funkcija Coseno ARC uporablja za določitev kota.

Rezultati se lahko v decimalcih nekoliko razlikujejo, glede na zaokroževanje.

Rešitev c

Obod P je kontura slike, enakovredna vsoti ukrepov treh strani:

P = 22.96 + 38.00 + 45.80 = 106.76 samovoljne enote.

Rešitev d

Formula za izračun območja katerega koli trikotnika je:

A = (1/2) x Osnovna x višina

Izbrati moramo eno od strani kot bazo in določiti višino. Na primer izbira strani, ki meri 45.8, narišemo višino h Do Vertexa A, ki je rdeča črta na sliki 2b.

S tem razdelimo originalni trikotnik na dva pravokotnika, oba z h Kot pogost cateto. Kateri koli od njih služi, saj poznamo ostro stran in kot.

Vzeli bomo tistega, ki ima hipotenuso, ki je enaka 38, kategorijo, ki meri h, ki je iskana višina in akutni kot, enak 30 °.

S pomočjo trigonometričnih razlogov akutnega kota 30 ° določimo vrednost h:

Sen 30º = cateto nasproti 30 ° / hipotenusa = h / 38

H = 38 x Sen 30 ° = 19

Zato:

A = (1/2) x 45.8 x 19 = 435.1 samovoljna območja območja.

Lahko bi izbrali drugo stran kot podlago, na primer stran 38, v tem primeru višina h Drugače je, saj nastane še en pravokotnik trikotnik, vendar je rezultat območja enak. Ostaja kot vaja, da ga bralec preveri.

- Vaja 3

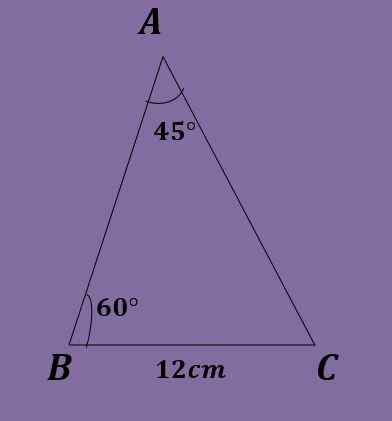
Glede na ABC trikotnik, ki je A = 45 °, B = 60 ° in A = 12 cm, izračunajte druge podatke o trikotniku.

Vam lahko služi: znaki združevanja

Rešitev

Uporaba vsote notranjih kotov trikotnika je enaka 180 °, ki mora:

C = 180º-45º-60 ° = 75 °.

Trije koti so že znani. Nato uporabimo zakon o dojki za izračun obeh strani, ki manjkata.

Enačbe, ki nastanejo, so 12 / brez (45 °) = b / brez (60 °) = c / brez (75 °).

Od prve enakosti lahko očistite "B" in to pridobite:

b = 12*brez (60 °)/brez (45 °) = 6√6 ≈ 14.696cm.

Prav tako lahko počistite "C" in to dobite:

C = 12*sin (75 °)/sin (45 °) = 6 (1+√3) ≈ 16.392cm.

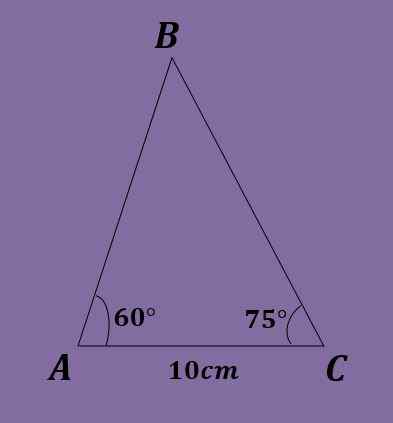
- Vaja 4

Glede na trikotnik ABC tako, da je A = 60 °, C = 75 ° in B = 10 cm, izračunajte druge podatke o trikotniku.

Rešitev

Kot v preteklem letu morate B = 180 °-60 °-75 ° = 45 °. Poleg tega z zakonom o dojki morate do / brez (60 °) = 10 / brez (45 °) = c / brez (75 °), kjer je mogoče dobiti, da je A = 10*brez (60 °) / brez (45 °) = 5 √6 ≈ 12.247 cm in c = 10*sin (75 °)/brez (45 °) = 5 (1+√3) ≈ 13.660 cm.

- Vaja 5

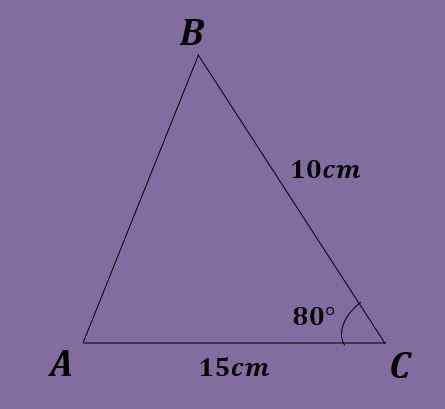
Glede na trikotnik ABC tako, da je A = 10cm, B = 15cm in C = 80 °, izračunajte druge podatke o trikotniku.

Rešitev

V tej vaji je znan le kot, zato ni mogoče začeti, kot je bilo to v obeh prejšnjih vajah. Poleg tega zakona o dojki ni mogoče uporabiti, ker nobene enačbe ni bilo mogoče rešiti.

Zato se uporablja zakon o Cosenosu. Moraš:

C² = 10²+15² - 2 (10) (15) cos (80 °) = 325 - 300*0.173 ≈ 272.905 cm,

Tako da c ≈ 16.51 cm. Zdaj, ko poznamo tri strani, se uporablja zakon o dojki in pridobi se:

10 / brez (a) = 15 / brez (b) = 16.51cm /brez (80 °).

Od tod, kadar je jasno b ​​brez (b) = 15*brez (80 °)/ 16.51 ≈ 0.894, kar pomeni, da je b ≈ 63.38 °.

Zdaj je mogoče dobiti, da je a = 180 ° - 80 ° - 63.38 ° ≈ 36.62 °.

- Vaja 6

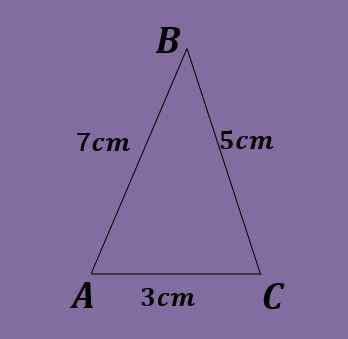
Strani poševnega trikotnika so a = 5 cm, b = 3 cm in c = 7cm. Izračunajte kote trikotnika.

Rešitev

Ponovno zakona o dojki ni mogoče uporabiti neposredno, saj nobena enačba ne bi služila vrednosti kotov.

Uporaba zakona kosinusa morate c² = a² + b² - 2ab cos (c), od koder ko so cos (c) = (a² + b² - c²)/ 2ab = (5² + 3² -7²)/ 2*5) *3 = -15/30 = -1/2 in zato c = 120 °.

Zdaj je mogoče uporabiti zakon o dojki in tako pridobiti 5/brez (a) = 3/brez (b) = 7/brez (120 °), kjer je mogoče B očistiti B in ga pridobiti brez (b) = 3* brez (120 ° )/7 = 0.371, tako da je B = 21.79 °.

Končno se zadnji kot izračuna s pomočjo A = 180 °-130 °-21.79 ° = 38.21.

Reference

1. Clemens, s. Geometrija z aplikacijami. Addison Wesley.
2. Ibáñez, str. 2010. Matematika III. Cengage učenje.
3. Jiménez, r. Matematika II: geometrija in trigonometrija. 2. mesto. Izdaja. Pearson.
4. Matematika za vas. OBTUSE TRIKANJE. Okrevano od: matematika za.WordPress.com.
5. Stewart, J. 2007. Prekalenkulacija. 5. Izdaja. Cengage učenje.