Triangles Zgodovina, elementi, klasifikacija, lastnosti

The Trikotniki So ravne in zaprte geometrijske figure, ki so sestavljene iz treh strani. Trikotnik je določeno s tremi črtami, ki se razrežejo dve do dve, ki se med seboj tvorijo trije koti. Trikotna oblika, polna simbolike, je prisotna v neštetih predmetih in kot element konstrukcije.

Izvor trikotnika je izgubljen v zgodovini. Iz arheoloških dokazov je znano, da ga primitivno človeštvo dobro pozna, saj arheološki ostanki potrjujejo, da je bil uporabljen v orodjih in orožju.

Slika 1. Trikotniki. Vir: Javne domene.

Očitno je tudi, da so stari Egipčani imeli trdno znanje o geometriji in zlasti o trikotni obliki. Utelešeni so bili v arhitekturnih elementih svojih monumentalnih konstrukcij.

V RHIND papirusu obstajajo formule za izračun trikotnikov in trapeznih območij, pa tudi nekaj zvezkov in drugih konceptov rudimentarne trigonometrije.

Po drugi strani je znano, da so Babilonci uspeli izračunati območje trikotnika in druge geometrijske figure, ki so jih uporabljali v praktične namene, kot so delitve zemlje. Prav tako so se zavedali številnih lastnosti trikotnikov.

Vendar so bili stari Grki tisti, ki so danes sistematizirali številne pogoste geometrijske koncepte, čeprav veliko tega znanja ni bilo izključno, saj so ga zagotovo delili s temi drugimi starodavnimi civilizacijami.

[TOC]

Elementi trikotnika

Elementi katerega koli trikotnika so navedeni na naslednji sliki. Obstajajo tri: točke, stranice in koti.

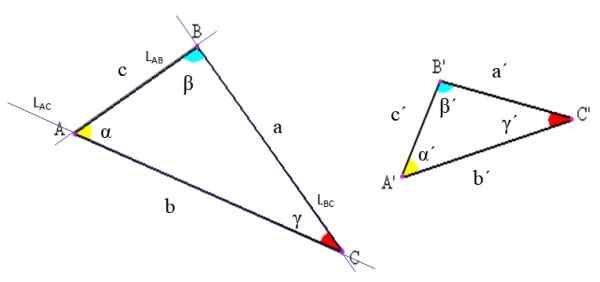Slika 2. Zapis trikotnikov in njihovih elementov. Vir: Wikimedia Commons, spremenjena s. Zapata

-Točke: To so točke križišča črt, katerih segmenti določajo trikotnik. Na primer na zgornji sliki črta l_AC ki vsebuje izmenični segment, preseka črto L_Ab ki vsebuje segment AB tik v točki A.

-Strani: Med vsakim nekaj vrhovi je narisan linijski segment, ki predstavlja eno stran trikotnika. Ta segment je mogoče označiti s črkami koncev ali z določeno črko, da ga pokličete. Na primeru slike 2 se AB stran imenuje tudi "C".

-Koti: Med vsako stranjo s skupno točko izvira kot, katerega vrha sovpada s trikotnikom. Kot je na splošno označen z grško črko, kot je navedeno na začetku.

Če želite zgraditi določen trikotnik, z določeno obliko in velikostjo, imate le nekaj naslednjih naborov podatkov:

-Tri strani, precej očitne v primeru trikotnika.

-Dve strani in kot med njima, preostala stran pa je takoj narisana.

-Dva kota (notranja) in stran med njima. S podaljšanjem sta narisani dve manjkajoči strani in trikotnik je pripravljen.

Zapis

Na splošno v zapisu trikotnikov se uporabljajo naslednje konvencije: točki so označeni z velikimi črkami, stranice z drobnimi latinskimi črkami in koti z grškimi črkami (glej sliko 2).

Na ta način je trikotnik poimenovan v skladu s svojimi tolici. Na primer, trikotnik na levi na sliki 2 je trikotnik ABC, tisti na desni pa je trikotnik a'b'c '.

Možno je tudi uporabiti druge zapise; Na primer, kot α na sliki 2 je označen kot BAC. Upoštevajte, da je črka vrha na sredini in črke so zapisane v nasprotni smeri igle ure.

Lahko vam služi: razmejitev problema

Drugič je nameščen naglas Circumflex, da označuje kot:

Ali se uporablja simbol ∠, saj prejšnji zapis morda ni enostaven v tisku, čemur sledi črka, ki ustreza točki:

α = ∠A

Vrste trikotnikov

Obstaja več meril za klasifikacijo trikotnikov. Najbolj običajno je, da jih razvrstimo glede na ukrep svojih strani ali glede na ukrep njihovih kotov. Trikotniki so lahko odvisno od mere njihovih strani: skale, izoscele ali enakostranski:

-Scalene: Njene tri strani so različne.

-Izosceles: Ima dve različni strani in eno.

-Enakostranično: Tri strani so enake.

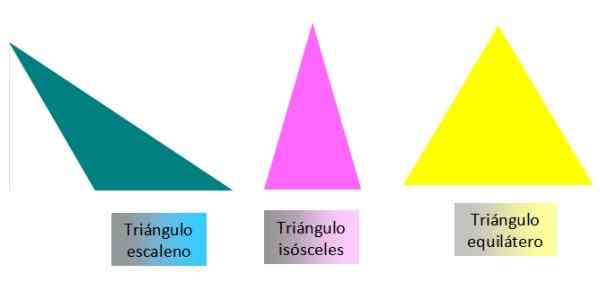Slika 3. Razvrstitev trikotnikov na njihovih straneh. Vir: f. Zapata

Glede na ukrep njihovih kotov se trikotniki imenujejo tako:

-Obtuse, Če je eden od notranjih kotov večji od 90 °.

-Akutant, Ko so trije notranji koti trikotnika akutni, to je manj kot 90 °

-Pravokotnik, V primeru, da je eden od njegovih notranjih kotov vreden 90 °. Strani, ki tvorijo 90 °, se imenujejo catetos in nasprotna stran desnega kota je hipotenuza.

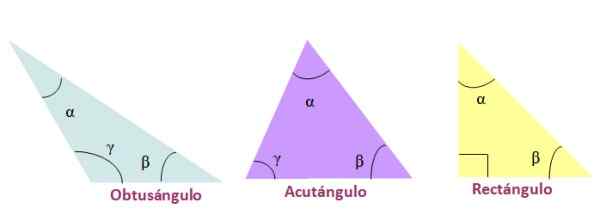Slika 4. Razvrstitev trikotnikov po njihovih notranjih kotih. Vir: f. Zapata.

Skladnost trikotnikov

Ko imata dva trikotnika enake oblike in sta enake velikosti. Seveda je skladnost povezana z enakostjo, zakaj torej v geometriji govorimo o "dveh skladnih trikotnikih" namesto o "dveh enakih trikotnikih"?

No, najraje je, da se izraz "skladnost" drži resnice, saj imata dva trikotnika lahko enako obliko in velikost, vendar sta v ravnini drugače usmerjena (glej sliko 3). Z vidika geometrije ne bi bili več strogo enaki.

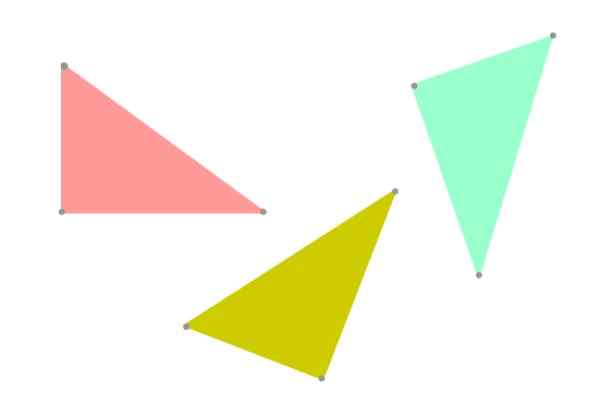Slika 5. Skladni trikotniki, vendar ne nujno enaki, ker je njegova orientacija v ravnini drugačna. Vir: f. Zapata.

Merila za skladnost

Dva trikotnika sta skladna, če se zgodi katera od naslednjih situacij:

-Tri strani merijo enako (spet je to najbolj očitno).

-Imata dve enaki strani in z enakim kotom med njima.

-Oba imata dva enaka notranja kota in stran med temi koti je enaka.

Kot je razvidno, gre za približno dva trikotnika, ki izpolnjujeta potrebne pogoje, tako da sta njihovi obliki in velikost popolnoma enaki.

Merila za skladnost so zelo koristna, saj je treba v praksi nešteto mehanskih delov in delov izdelati zaporedno, tako da so njihovi ukrepi in oblika popolnoma enaki.

Podobnost trikotnikov

Trikotnik je podoben drugemu, če imajo enako obliko, tudi če so različne velikosti. Da bi zagotovili, da je oblika enaka, je potrebno, da imajo notranji koti enako vrednost in da so stranice sorazmerne.

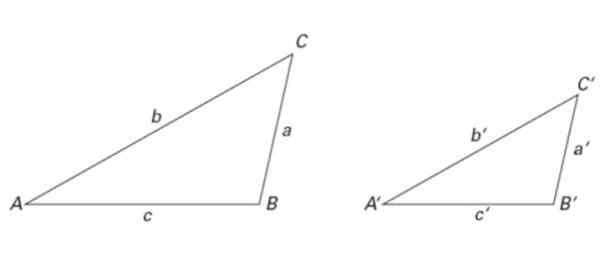Slika 6. Dva podobna trikotnika: njihove velikosti se razlikujejo, vendar so njihovi deleži enaki. Vir: f. Zapata.

Tudi trikotniki slike 2 so podobni, pa tudi tisti na sliki 6. Tako:

∠ a = ∠ A ', ∠ B = ∠ B 'in ∠ C = ∠ C '

Kar zadeva strani, so izpolnjeni naslednji razlogi za podobnost:

a/a '= b/b' = c/c '

Lastnosti

Temeljne lastnosti trikotnikov so naslednje:

-Vsota notranjih kotov katerega koli trikotnika je vedno 180 °.

-Za vsak trikotnik je vsota njegovih zunanjih kotov enaka 360 °.

Lahko vam služi: Osnovne raziskave: značilnosti, definicija, primeri

- Zunanji kot trikotnika je enak vsoti obeh notranjih kotov, ki nista v bližini tega kota.

Teoreme

Prvi teorem takega

Pripisujejo grškemu filozofu in matematiki zgodbe o Miletu, ki so razvili več teoremov, povezanih z geometrijo. Prvi od njih vzpostavi naslednje:

Če več vzporednih linij razreže dve prečni črti, določijo segmente, ki so sorazmerni.

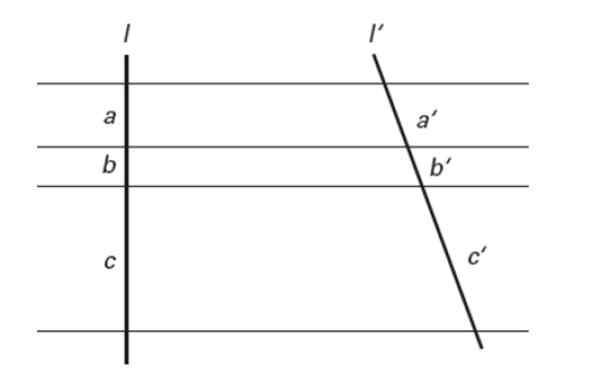Slika 7. Teorem zgodb. Vir: f. Zapata.

Z drugimi besedami:

a/a '= b/b' = c/c '

Prvi teorem takega velja za trikotnik, na primer je na levi strani ABC modri trikotnik, ki ga razrežejo rdeči vzporednici na desni:

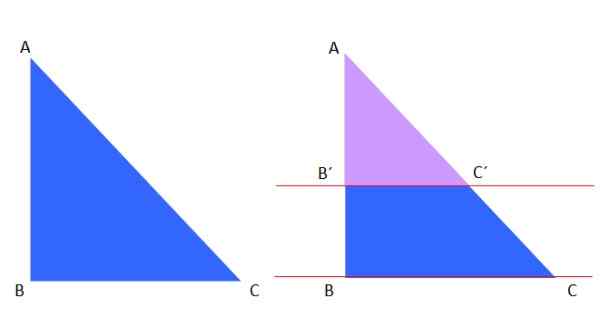Slika 8. Teorem takšnih in podobnih trikotnikov.

Vijolični trikotnik vijolične trikotnike je podoben modremu trikotniku ABC, zato je po takšnem izrek napisano naslednje:

Ab '/ac' = ab/ac

In je skladno s tem, kar je bilo razloženo zgoraj v segmentu podobnosti trikotnikov. Mimogrede, vzporedne črte so lahko tudi navpične ali vzporedne s hipotenuzo in podobni trikotniki dobijo.

Drugi teorem tega

Ta teorem se nanaša tudi na trikotnik in obod središča ali, kot je prikazan spodaj. Na tej sliki je AC premer oboda in B je točka, saj je B drugačen od A in B.

Drugi izrek takšnih držav, ki:

Kot med segmenti AB in BC je vedno 90 °, zato je trikotnik ABC pravokotnik.

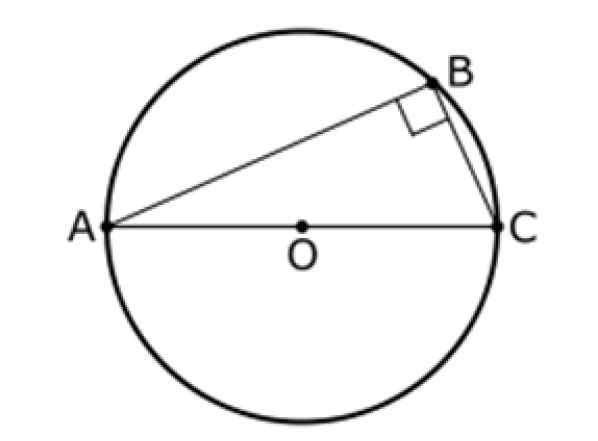Slika 9. Drugi teorem takega. Vir: Wikimedia Commons. Inductiveload [javna domena].

Teorem za pitagore

To je eden najbolj znanih teoremov v zgodovini. Je posledica grške matematične pitagore samos (569 - 475 do. C.) in je uporabna za pravi trikotnik. Pravi tako:

Vsota kvadratov dolžin kategorij trikotnika pravokotnika je enaka dolžini hipotenuze visoko do kvadrata.

Če kot primer vzamemo modri trikotnik slike 8 ali vijolični trikotnik, kot sta oba pravokotna, potem lahko rečemo:

AC² = Ab² + Pr² (Modri ​​trikotnik)

Ac '² = Ab '² + Pr. '² (Vijolični trikotnik)

Območje trikotnika

Območje trikotnika daje produkt njegove baze do in njena višina h, deljeno z 2. In s trigonometrijo lahko to višino zapišemo kot H = b sinθ.

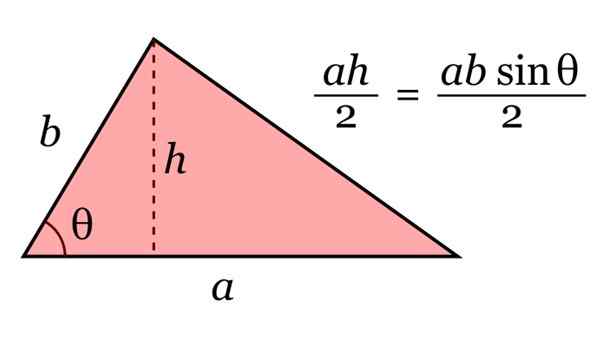Slika 10. Območje trikotnika. Vir: Wikimedia Commons.

Primeri trikotnikov

Primer 1

Rečeno je, da je s svojim prvim teoremom uspelo izmeriti višino velike piramide v Egiptu, eno od sedmih čudes starodavnega sveta, ki je meril senco, ki jo je projicirala na tleh, in tiste tla.

To je shema postopka, ki mu sledi:

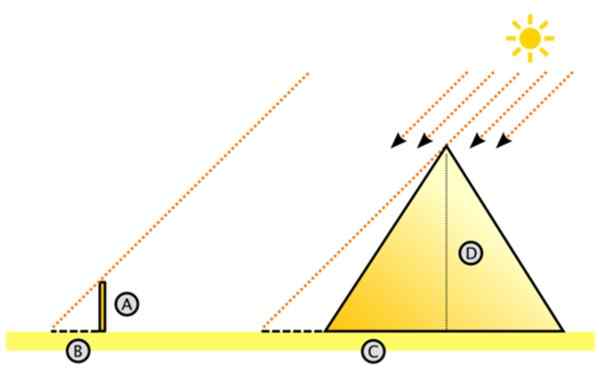Slika 11. Shema za merjenje višine velike piramide s podobnostjo trikotnikov. Vir: Wikimedia Commons. DAKE [CC BY-SA 3.0 (http: // creativeCommons.Org/licence/by-sa/3.0/]]

Tako upravičeno je domnevno, da sončni žarki vplivajo na vzporedni. Glede na to si je predstavljal velik desni trikotnik.

Obstaja višina piramide in C je razdalja na tleh, merjena od središča do sence, ki jo projicira piramida na puščavskem tleh. Morda je naporno meriti C, vendar je vsekakor lažje kot merjenje višine piramide.

Na levi je majhen trikotnik, iz mačk A in B, kjer je a višina kolčka, ki se je navpično zataknila na tleh in B je senca, ki jo projecira. Obe dolžini sta merljivi, tako kot C (C je enak dolžini sence + polovica dolžine piramide).

Vam lahko služi: kaj so taktilni dražljaji?

Nato po podobnosti trikotnikov:

A/b = d/c

In višina velike piramide se izkaže za: D = C.(A/B)

Primer 2

Civilni gradbeni oklep so konstrukcije, ki temeljijo na tanko -lesenih ali kovinskih ravnih palicah, ki se uporabljajo kot podpora v mnogih stavbah. Znani so tudi kot rešetke, rešetke ali retikulirane (TRUSS v angleščini).

V njih so vedno prisotni trikotniki, ker so palice medsebojno povezane na točkah, imenovanih vozlišči, ki jih je mogoče fiksirati ali artikulirati.

Slika 12. Trikotnik je prisoten v okvirju tega mostu. Vir: pxhere.

Primer 3

Metoda, znana kot triangulacija, vam omogoča, da pridobite lokacijo nedostopnih točk, ki poznajo druge lažje razdalje za merjenje, pod pogojem, da se oblikuje trikotnik, ki med njenimi točki vključuje želeno lokacijo.

Na primer, na naslednji sliki želite vedeti, v kakšnem trenutku je morje ladja, označena kot B.

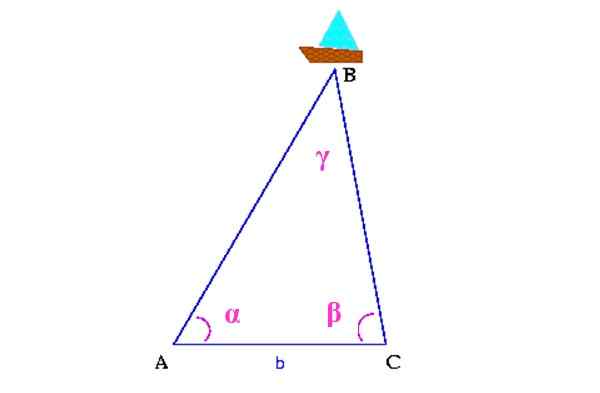Slika 13. Shema triagulacije za iskanje ladje. Vir: Wikimedia Commons. Colette [cc by-sa 3.0 (http: // creativeCommons.Org/licence/by-sa/3.0/]]

Najprej se meri razdalja med dvema točkama na obali, ki sta na sliki a in c. Potem morate s pomočjo a s pomočjo a določiti kota α in β teodolit, Naprava, ki služi za merjenje navpičnih in vodoravnih kotov.

Z vsemi temi informacijami je zgrajen trikotnik, na katerem je zgornja vrha ladja. Znižal bi kota γ.

Vaje

Vaja 1

Na prikazani sliki so sončni žarki vzporedni. Na ta način 5 -metrsko visoko drevo načrtuje 6 -metrsko senco na tleh. Hkrati je senca stavbe 40 metrov. Po takšnem teoremu poiščite višino stavbe.

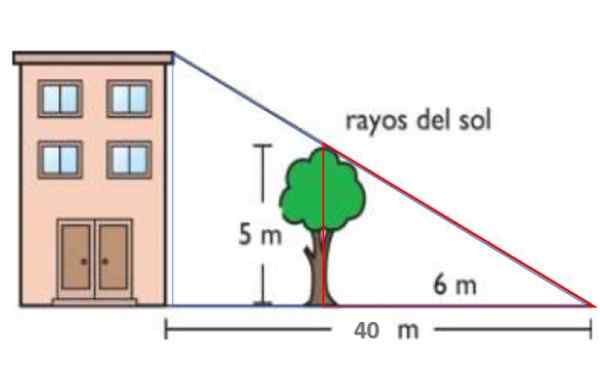Slika 14. Shema za leto rešena 1. Vir: f. Zapata.

Rešitev

Rdeči trikotnik ima strani 5 oziroma 6 metrov, medtem ko ima modra višino H - višino stavbe in osnove 40 metrov. Oba trikotnika sta torej podobna:

H / 40 = 5/6 → H = 40.(5/6) M = 33.3 m

Vaja 2

Poznati morate vodoravno razdaljo med dvema točkama Do in B, Toda nahajajo se na zelo nepravilnem terenu.

Približno v sredini (P_m) Iz te dežele izstopa znamenitost.75 metrov visok. Če ukrep traku označuje dolžino 26 metrov, merjeno od A do vida, in 27 metrov od B do iste točke, poiščite razdaljo Ab.

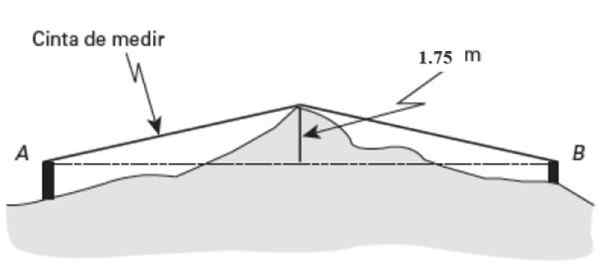Slika 15. Shema za rešeno vajo 2. Vir: Jiménez, R. Matematika II. Geometrija in trigonometrija.

Rešitev

Teorem Pythagora se nanaša na enega od dveh pravokotnikov na sliki. Začenši s tisto na levi:

Hipotenuse = c = 26 metrov

Višina = a = 1.75 metrov

Ap_m = (26² - 1.75²)^1/2 = 25.94 m

Zdaj se pitagora uporablja v desnem trikotniku, tokrat c = 27 metrov, a = 1.75 metrov. S temi vrednostmi:

Bp_m= (27² - 1.75²)^1/2 = 26.94 m

Razdalja AB dodaja te rezultate:

AB = 25.94 m +26.94 m = 52.88 m.

Reference

1. Baldor, j. Do. 1973.Ravna in vesoljska geometrija. Srednjeameriška kulturna.
2. Barredo, d. Geometrija trikotnika. Okreval od: ficus.pntic.Mec.je.
3. Jiménez, r. 2010. Matematika II. Geometrija in trigonometrija. Druga izdaja. Pearson.
4. Wentworth, g. Geometrija planeta. Okreval od: Gutenberg.org.
5. Wikipedija. Trikotnik. Okrevano od: je. Wikipedija.org.