Trikotnik Scalene

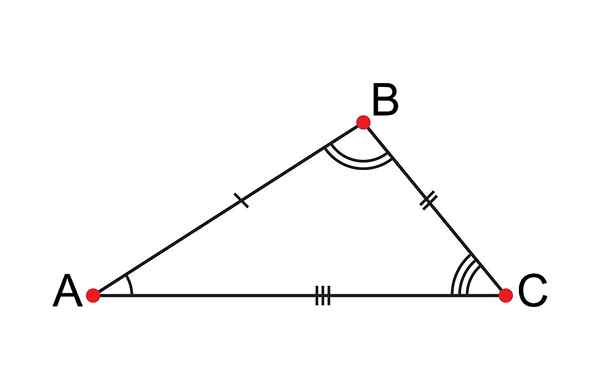
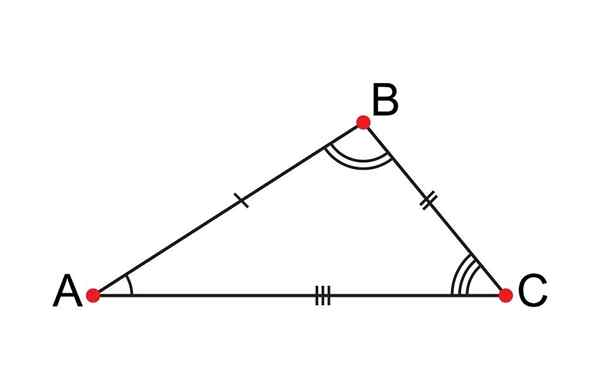Scalene Trikotnik ima vse svoje neenake strani

Kaj je skalni trikotnik?

A Trikotnik Scalene Gre za tristranski poligon, kjer imajo vsi različne ukrepe ali dolžine; Iz tega razloga je dobilo ime Escaleno, kar v latinščini pomeni neenako.

Trikotniki so poligoni, ki se v geometriji štejejo za najpreprostejše, ker tvorijo tri strani, tri kote in tri točke. V primeru Scalene trikotnika za vse različne strani pomeni, da bodo tudi njeni trije koti.

Značilnosti lestvice trikotnikov

Trikotniki v lestvici so preprosti poligoni, ker nobena od njegovih strani ali kotov nima enake mere, za razliko od izoscelov in ravnotežnih trikotnikov.

Ker imajo vse njihove strani in koti različne ukrepe, se ti trikotniki štejejo za nepravilne konveksne poligone.

Glede na amplitudo notranjih kotov so Scalene trikotniki razvrščeni kot:

• Trikotnik pravokotnika Scalene: Vse njegove strani so različne. Eden od njegovih kotov je naravnost (90^tudi), drugi pa so akutni in z različnimi ukrepi.
• Trikotnik Scalene obtuse: Vse njene strani so različne in eden od njegovih kotov je nejasno (> 90^tudi).
• Trikotnik Acutangle Scalene: Vse njegove strani so različne. Vsi njegovi koti so akutni (< 90^tudi), Z različnimi ukrepi.

Druga značilnost Scalene Triangles je ta, da je zaradi neskladnosti.

Komponente/elementi

Mediana

To je črta, ki pušča od sredine točke na eni strani in doseže nasprotno vrhovo. Trije mediji se udeležujejo na točki, imenovani Baricentro ali Centroid.

Bisektor

To je polčas, ki deli vsak kot na dva kota enakega merila. Bisektorji trikotnika se strinjajo v točki, imenovani kongres.

Mediatrix

Gre za segment, pravokoten na stran trikotnika, ki izvira iz sredine tega. V trikotniku so tri mediatrice in se udeležite na točki, imenovani Pourcecentro.

Višina 

To je črta, ki sega od točke na nasprotno stran, in tudi ta črta je pravokotna na to stran. Vsi trikotniki imajo tri višine, ki sovpadajo v točki, imenovani Ortotenter.

Lastnosti Escaleno Triange

Trikotniki lestvice so opredeljeni ali identificirani, ker imajo več lastnosti, ki jih predstavljajo, izvirajo iz teoremov, ki jih predlagajo veliki matematiki. So:

Notranji koti

Vsota notranjih kotov je vedno enaka 180^tudi.

Vsota strani

Vsota ukrepov dveh strani mora biti vedno večja od ukrepa tretje strani, A + B> C.

Neprimerne strani

Vse strani plezalnih trikotnikov imajo različne ukrepe ali dolžine; to pomeni, da so neprimerni.

Neprimerni koti

Ker so vse strani Scalene trikotnika drugačne, bodo tudi njeni koti. Vendar bo vsota notranjih kotov vedno enaka 180 °, v nekaterih primerih pa je lahko eden od njegovih zornih kotov obrobno ali naravnost, v drugih pa bodo vsi njeni koti akutni.

Vam lahko služi: multiplikativni problemi za otroke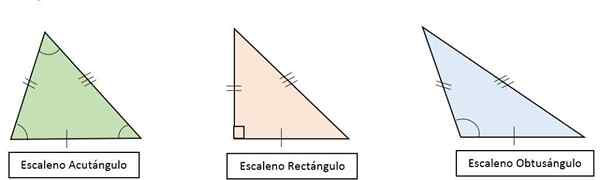 Vrste skalile trikotnikov glede na njihove kote

Višina, mediana, mediatrix in bisektor niso naključni

Kot vsak trikotnik ima tudi Escaleno različne črte, ki ga sestavljajo, kot so: višina, srednja, mediatrix in bisektor.

Zaradi posebnosti svojih strani v tej vrsti trikotnika nobena od teh vrstic ne bo sovpadala v enem samem.

Orocentro, Baricentro, Inwentro in OCCENTRO niso naključni

Tako kot višina, mediana, Bisector in Mediatrix predstavljajo različni segmenti linij, v trikotniku Scalene so se sestanke -Ortocenter, Inwenter in Occucentro Baricenter -bodo na različnih točkah (to pomeni, da ne sovpadajo).

Ortocenter ima odvisno od tega, ali je trikotnik akutant, pravokotnik ali obtuse, različne lokacije:

do. Če je trikotnik akutant, bo ortocenter znotraj trikotnika.

b. Če je trikotnik pravokotnik, bo ortocenter sovpadal z vrhom na ravni strani.

c. Če je trikotnik nejasni, bo ootocenter zunaj trikotnika.

Relativne višine

Višine so glede na stranice.

V primeru Scalene Trikotnika bodo imeli te višine različne ukrepe. Vsak trikotnik ima tri relativne višine in za njihovo izračun se uporablja Herónova formula.

Izračun oboda, območje, višina in stranice

Kako izračunati obod?

Obod poligona se izračuna v vsoti strani.

Kot v tem primeru ima Scalene Triangle vse strani z drugačnim ukrepom, bo njegov obod:

P = stran do + stran b + stran c.

Kako izračunati območje?

Trikotniki se vedno izračunajo z isto formulo, pomnožijo bazo po višini in delijo dva:

Območje = (osnova _* H) ÷ 2

V nekaterih primerih višina Scalene trikotnika ni znana, vendar obstaja formula, ki jo je predlagal matematik Herón, da bi izračunali območje, ki pozna ukrep treh strani trikotnika.

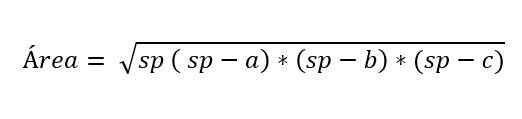
Kje:

• A, b in c predstavljajo stranice trikotnika.
• SP ustreza polperimetru trikotnika, torej polovice oboda:

sp = (a + b + c) ÷ 2

V primeru, da je mogoče imeti samo dve strani trikotnika in kota, ki se oblikujeta med njima. Tako moraš:

Območje = (stran _* H) ÷ 2

Kjer je višina (h) izdelek na eni strani skozi nasprotni kot. Na primer, za vsako stran bo območje:

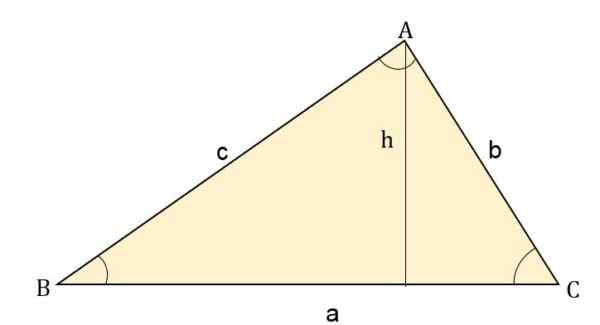
• Območje = (b _* c _* greh a) ÷ 2
• Območje = (a _* c _* greh b) ÷ 2.
• Območje = (a _* b _* Sen c) ÷ 2

Kako izračunati višino?

Kot vse strani Scalene Trikotnika so drugačne, tudi višine s teoremom pitagore ni mogoče izračunati.

Iz Herónove formule, ki temelji na ukrepih treh strani trikotnika, je mogoče izračunati območje.

Vam lahko služi: faktorski zapis: koncept, primeri in vaje

Višina je lahko jasna iz splošne formule območja:

Formula za izračun višine skalenega trikotnika

Stran je nadomeščena z mero strani A, B ali C.

Drug način za izračun višine, ko je znana vrednost enega od zornih kotov, je uporaba trigonometričnih razlogov, kjer bo višina predstavljala trikotni cateto.

Na primer, ko je znan nasprotni kot višine, ga bo določila dojka:

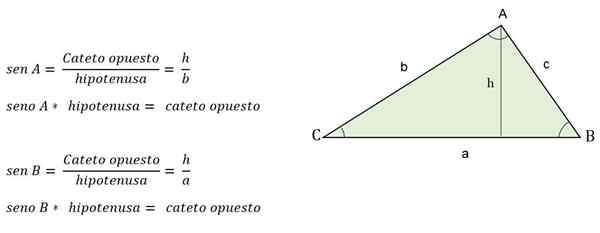Trigonometrična formula za izračun višine trikotnika skale

Kako izračunati strani?

Ko imate ukrep dveh strani in kota, ki nasprotuje temu, je mogoče določiti tretjo stran, ki uporablja teorem Cosenosa.

Na primer, v AB trikotniku je narisana višina glede na izmenični segment. Na ta način je trikotnik razdeljen na dva trikotnika pravokotnika.

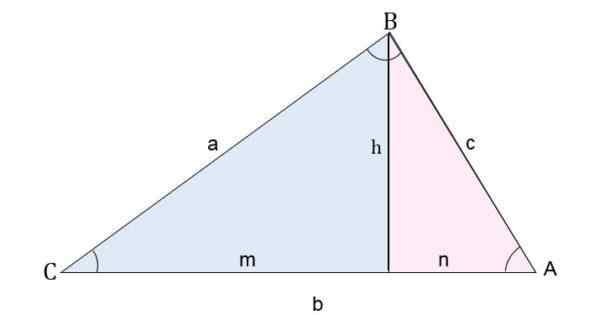Delitev skalenskega trikotnika v dva pravokotnika za izračun stranic

Za izračun strani C (segment AB) se uporablja teorem pitagore za vsak trikotnik:

• Za modri trikotnik morate:

c² = h² + m²

Kot M = B - N, se nadomesti:

c² = h² + b² (B - n)²

c² = h² + b² - 2bn + n².

• Za roza trikotnik morate:

h² = a² - n²

Nadomeščen je v prejšnji enačbi:

c² = a² - n² + b² - 2bn + n²

c² = a² + b² - 2bn.

Vedoč, da n = a _* Cos C, se nadomesti v prejšnji enačbi in dobimo vrednost stranske C:

c² = a² + b² - 2B_* do _* cos c.

Z zakonom o Ponosovi lahko stranice izračunamo kot:

• do² = b² + c² - 2B_* c _* stvari.
• b² = a² + c² - 2. mesto_* c _* cos b.
• c² = a² + b² - 2B_* do _* cos c.

Obstajajo primeri, ko ukrepi na strani trikotnika niso znani, ampak njena višina in koti, ki se oblikujejo v vrhovih. Za določitev območja v teh primerih je treba uporabiti trigonometrične razloge.

Če poznate kot ene od svojih točk, se identificira kategorija in uporabljen je ustrezen trigonometrični razlog:

Trigonometrična formula za izračun stranic skale trikotnika

Na primer, Cateto AB bo nasproten kot C, vendar meji na kot A. Odvisno od strani ali noge, ki ustreza višini, je druga stran očiščena, da dobimo vrednost tega.

Rešene vaje

Prva vaja

Izračunajte območje in višino trikotnika Escalano ABC, vedoč, da so njene strani:

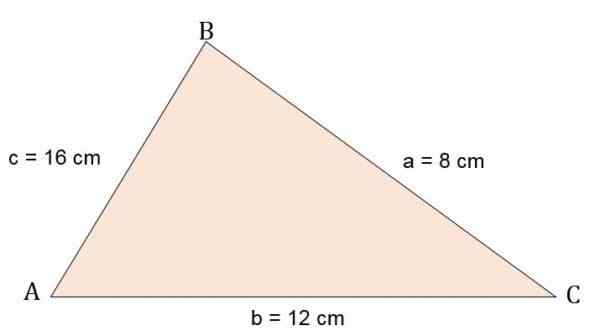
A = 8 cm.

B = 12 cm.

C = 16 cm.

Rešitev

Ker so podatki dani ukrepi treh strani trikotnika Scalene.

Ker nimate vrednosti višine, lahko območje določite z uporabo Herónove formule.

Najprej se izračuna polperimeter:

sp = (a + b + c) ÷ 2

sp = (8 cm + 12 cm + 16 cm) ÷ 2

sp = 36 cm ÷ 2

sp = 18 cm.

Zdaj so vrednosti v Herónovi formuli zamenjane:

Vam lahko služi: absolutna frekvenca: formula, izračun, porazdelitev, primer Herónova formula

Če poznate območje, je mogoče izračunati relativno višino do strani B. Iz splošne formule, ki jo razčistite:

Območje = (stran _* H) ÷ 2

46, 47 cm² = (12 cm _* H) ÷ 2

H = (2 _* 46,47 cm²) ÷ 12 cm

H = 92,94 cm² ÷ 12 cm

H = 7,75 cm.

Druga vaja

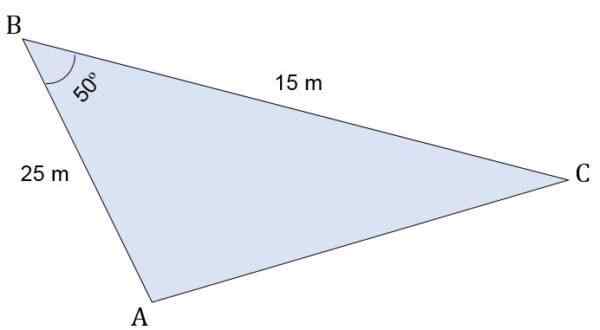
Glede na trikotnik ABC Escalano, katerega ukrepi so:

• Segment ab = 25 m.
• Segment BC = 15 m.

V točki B nastane kot 50 °. Izračunajte višino glede na stran C, obod in površino tega trikotnika.

Rešitev

V tem primeru obstajata dva stranska ukrepa. Za določitev višine je treba izračunati merilo tretje strani.

Ker je dana stran dana nasprotni kot, je mogoče uporabiti zakon o Cosenosu za določitev ukrepa AC (b) strani:

b² = a² + c² - 2. mesto_*c _* cos b

Kje:

A = bc = 15 m.

C = AB = 25 m.

B = ac.

B = 50^tudi.

Podatki so zamenjani:

b² = (15)² + (25)² - 2_*(petnajst)_*(25) _* cos 50

b² = (225) + (625) - (750) _* 0,6427

b² = (225) + (625) - (482,025)

b² = 367,985

B = √367,985

B = 19,18 m.

Ker že imate vrednost treh strani, se izračuna obod tega trikotnika:

P = stran do + stran b + stran c

P = 15 m + 25 m + 19, 18 m

P = 59,18 m

Zdaj je mogoče določiti območje z uporabo Herónove formule, najprej pa je treba izračunati polperimeter:

sp = p ÷ 2

sp = 59,18 m ÷ 2

sp = 29,59 m.

Ukrepi strani in polperimetra v Herónovi formuli so zamenjani:

Končno, če poznamo območje, lahko relativno višino izračunamo na stran c. Iz splošne formule, ki jo morate očistiti, morate:

Območje = (stran _* H) ÷ 2

143,63 m² = (25 m _* H) ÷ 2

H = (2 _* 143,63 m²) ÷ 25 m

H = 287,3 m² ÷ 25 m

H = 11,5 m.

Tretja vaja

V trikotniku Escaleno ABC B strani meri 40 cm, C Side meri 22 cm, v točki A pa je kot 90 kot 90^tudi. Izračunajte območje tega trikotnika.

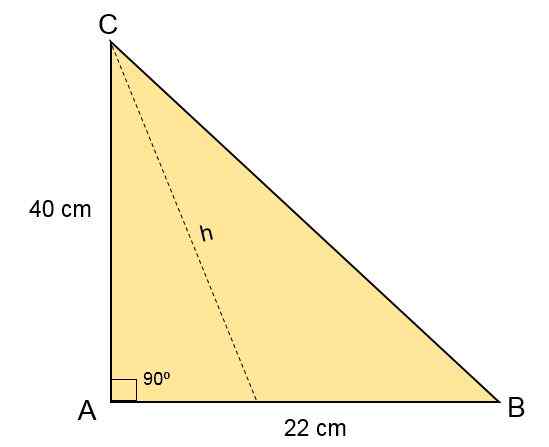
Rešitev

V tem primeru so podani ukrepi dveh strani trikotnika ABC lestvice, pa tudi kot, ki se oblikuje v točki do.

Za določitev območja ni treba izračunati ukrepa strani A, saj se skozi trigonometrične razloge uporabi kot, da ga najdemo.

Ker je na višini znan nasprotni kot, bo to določil izdelek na eni strani in prsi kota.

Zamenjava v formuli območja morate:

• Območje = (stran _* H) ÷ 2
• H = c _* greh a

Območje = (b _* c _* greh a) ÷ 2

Območje = (40 cm _* 22 cm _* Sen 90) ÷ 2

Območje = (40 cm _* 22 cm _* 1) ÷ 2

Območje = 880 cm² ÷ 2

Območje = 440 cm².

Reference

1. Álvaro Rendón,. R. (2004). Tehnična risba: zvezek z dejavnostjo.
2. Ángel Ruiz, h. B. (2006). Geometrije. CR tehnološka, .
3. Angel, a. R. (2007). Elementarna algebra. Pearson Education,.
4. Baldor, a. (1941). Algebra. Havana: Kultura.
5. Barbosa, j. L. (2006). Ravna evklidska geometrija. Rio de Janeiro,.
6. Kokseter, h. (1971). Osnove geometrije. Mehika: Limusa-Wiley.
7. Daniel c. Aleksander, g. M. (2014). Osnovna geometrija za študente. Cengage učenje.
8. Harpe, str. d. (2000). Teme v teoriji geometrijske skupine. University of Chicago Press.