Značilnosti fizične poti, vrste, primeri in vaje

The Usmeritev v fiziki Krivulja opisuje mobilni telefon pri prehodu skozi zaporedne točke med svojim gibanjem. Ker to lahko sprejme nešteto različic, bodo tudi oni poti, ki jim lahko sledi mobilni telefon.

Če hodimo iz enega kraja v drugega, se lahko človek loti različnih poti in različnih načinov: peš po pločnikih po ulicah in avenijah ali pa pride z avtomobilom ali motociklom na avtocesti. Med vožnjo po gozdu lahko sprehajalec sledi zapleteni usmeritvi, ki vključuje zavoje, plezanje ali spuščanje navzgor in dokler večkrat ne gre skozi isto točko.

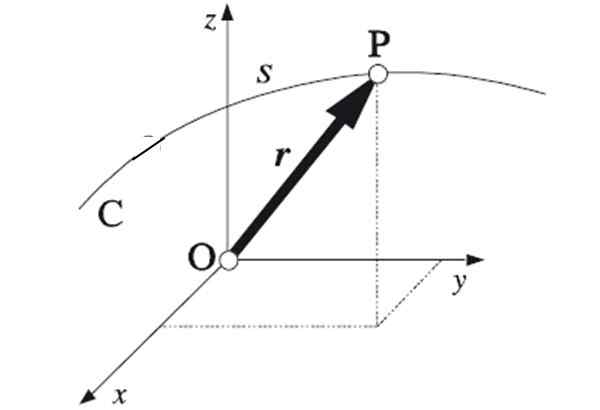Slika 1. Pridružite se ekstremne točke vsakega položaja vektorja, ki ji sledi delček. Vir: Algarabia [javna domena]

Če točke, skozi katere potuje mobilni telefon, sledijo ravni črti, bo usmeritev pravokotna. To je najpreprostejša usmeritev, ker je ena -dimenzijska. Za določitev položaja je potrebna ena koordinata.

Toda mobilni telefon lahko sledi potisni poti, ki ga je mogoče zapreti ali odpreti. V teh primerih je za spremljanje položaja potrebno dve ali tri koordinate. To so gibi v ravnini in prostoru. To je povezano z povezave: Omejevanje materialnih pogojev gibanja. Nekaj ​​primerov je:

- Orbite, ki opisujejo planete okoli sonca, so zaprte usmeritve v obliki elipse. Čeprav lahko v nekaterih primerih približno približajo krožno, kot v primeru Zemlje.

- Žoga, ki jo vratar brca v zadetku, sledi parabolični poti.

- Ptica v letu opisuje krivuljene usmeritve v vesolju, saj se lahko poleg premika po ravnini dvigne ali nižje po volji.

Fizična usmeritev je mogoče izraziti matematično, kadar je mobilni položaj znan kadar koli. Biti r Položaj vektor, ki ima koordinate x, in in z V najbolj splošnem primeru tridimenzionalnega gibanja. Poznavanje funkcije r (T) Traktor bo popolnoma določena.

[TOC]

Fantje

Na splošno je usmeritev lahko precej zapletena krivulja, še posebej, če želite matematično izraziti. Zato se začne z najpreprostejšimi modeli, kjer mobilniki potujejo po ravni črti ali na ravnini, ki je lahko tla ali kateri koli drug primerni:

Gibi v eni, dve in treh dimenzijah

Najbolj preučene usmeritve so:

- Pravokotni, Ko potujete po vodoravni, navpični ali nagnjeni črti. Kroglica, vržena navpično navzgor navzgor po tej poti ali predmetu, ki zdrsne navzdol z nagnjeno ravnino. So eno -dimenzionalni premiki, ena sama koordinata je dovolj, da popolnoma določi njegov položaj.

- Parabolična, v katerem mobilni telefon opisuje lok parabole. Pogost je, saj vsak objekt, ki se poševno sproži pod delovanjem gravitacije (izstrelki), sledi tej poti. Če želite določiti mobilni položaj, morate dati dve koordinati: x in in.

- Krožni, se pojavi, ko premikajoči delček sledi obodu. Pogosta je tudi po naravi in ​​vsakodnevni praksi. Številni vsakdanji predmeti sledijo krožni poti, kot so pnevmatike, koščki strojev in satelitov v orbiti, da navedejo nekaj primerov.

Vam lahko služi: Equinecent Vectors: definicija, zapis, vaje

- Eliptična, Predmet se premika po elipsi. Kot je navedeno na začetku, je usmeritev, ki jo planeti sledijo v orbiti okoli sonca.

- Hiperbolična, Astronomski predmeti pod delovanjem osrednje sile (gravitacija) lahko sledijo eliptični (zaprti) ali hiperbolični (odprti) usmeritvi, ki so manj pogosti kot prvi.

- Vijačno, o spiralno gibanje, kot pri ptici, ki se vzpenja v toplotnem toku.

- Zasuka ali nihala, Mobilec opisuje lok v okrožnih gibanjih.

Primeri

Usnjere, opisane v prejšnjem razdelku. Vsekakor je treba razjasniti, da je usmeritev mobilnega telefona odvisna od lokacije opazovalca. To pomeni, da je isti dogodek videti na različne načine, glede na to, kje je vsak.

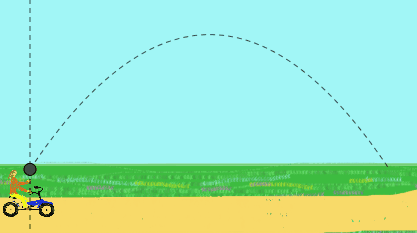
Na primer dekliška pedala s konstantno hitrostjo in vrže kroglico navzgor. Opaža, da žoga opisuje pravokotno usmeritev. 

Vendar bo za opazovalca, ki stoji na cesti, ki ga vidi, žoga imela parabolično gibanje. Zanj je bila žoga sprva vržena z nagnjeno hitrostjo, kar je posledica hitrosti dekličine roke in hitrosti kolesa.

Slika 2. Ta animacija prikazuje navpično izstrelitev žoge, ki jo je izdelala deklica, ki gre s kolesom, kot vidi (pravokotna usmeritev) in kot vidite opazovalca (parabolična pot). (Pripravil F. Zapata).

Usmeritev mobilnega telefona na izrecno, implicitno in parametrično

- Izrecno, neposredno določanje krivulje ali geometrijskega mesta, ki ga daje enačba in (x)

- Implicitno, v katerem je krivulja izražena kot f (x, y, z) = 0

-Parametrični, Na ta način se koordinate X in y Z pojavijo, odvisno od parametra, ki je na splošno izbran za čas t. V tem primeru je usmeritev sestavljena iz funkcij: x (t), in (t) in z (t).

Nato sta v kinematografiji podrobno opisani dve zelo preučeni usmeritvi: parabolična usmeritev in krožna usmeritev.

Lansiranje v vakuumu

Objekt (izstrelki) se vrže, ki tvori kot A z vodoravnim in z začetno hitrostjo v_tudi Kot prikazuje slika. Zračni odpor se ne upošteva. Gibanje lahko obravnavamo kot dva neodvisna in hkratna gibanja: eno vodoravno s konstantno in drugo navpično hitrostjo pod delovanjem gravitacije.

x (t) = x_tudi +v_vol.t

in (t) = y_tudi +v_Oy.T -½g.t²

Te enačbe so Parametrične enačbe izstrelitve projektila. Kot je razloženo zgoraj, imajo skupni parameter t, Kaj je čas.

V desnem trikotniku slike je razvidno:

v_vol = v_tudi cos θ_Yo

v_Oy = v_tudi greh θ_Yo

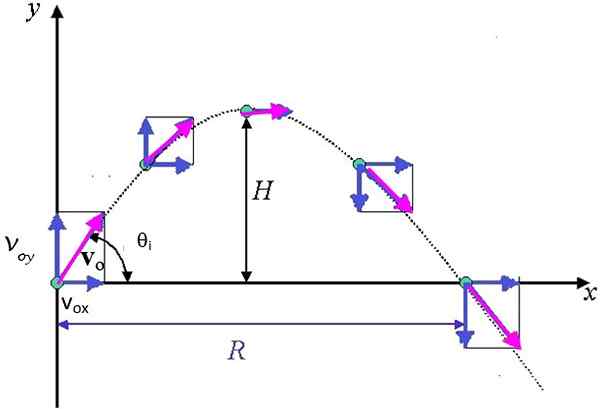Slika 3. Parabolična usmeritev, ki ji sledi izstrelki, ki prikazuje sestavne dele hitrosti vektorja. H je največja in R višina je največji vodoravni doseg. Vir: ayush12gupta [cc by-sa 4.0 (https: // creativeCommons.Org/licence/by-sa/4.0)]

Z zamenjavo teh enačb, ki vsebujejo kot izstrelitve v parametričnih enačbah, je:

Vam lahko služi: difrakcija zvoka: kaj je, primeri, aplikacije

x (t) = x_tudi +v_tudi cos θ_Yo.t

in (t) = y_tudi +v_tudi. greh θ_Yo.T -½g.t²

Parabolična enačba usmeritve

Izrecna enačba usmeritve je čiščenje t enačbe za x (t) in nadomeščanje v enačbi y (t) (t). Da bi olajšali algebrsko delo, je mogoče domnevati, da je izvor (0,0) na začetku in na ta način x_tudi = y_tudi = 0.

Po poenostavitvi parametra "t"Odpravljena je bila in enačba, ki ostaja, je in odvisna od X: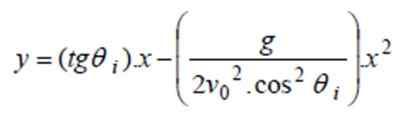

To je enačba usmeritve v Izrecna oblika.

Krožna usmeritev

Krožna usmeritev je podana z:

(X - x_tudi)² + (in - in_tudi)² = R²

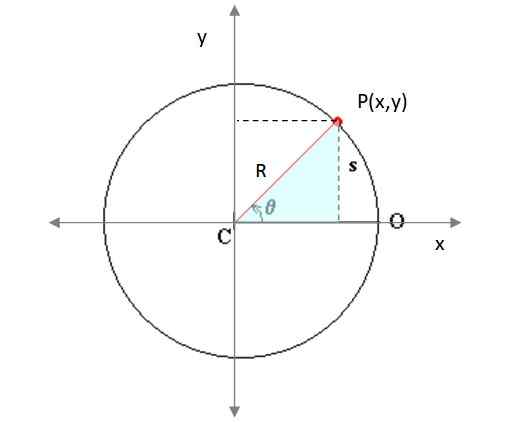Slika 4. Delček se premika v krožni poti na ravnini. Vir: Spremenjeno s F. Čevelj Wikimedia Commons.

Tukaj x_tudi in in_tudi Predstavljajo središče oboda, ki ga opisuje mobilni telefon, R pa je polmer istega. P (x, y) je točka poti. Iz zasenčenega trikotnika pravokotnika (slika 3) je opozorjeno, da:

x = r. cos θ

y = r. greh θ

Parameter je v tem primeru kot pometen kot θ, imenovan kotni premik. V posebnem primeru, da je kotna hitrost ω (kot, pometana na enoto časa), stalna, lahko potrdimo, da:

θ = θ_tudi + Ωt

Kjer θ_tudi To je začetni kotni položaj delca, ki je, če jemljemo kot 0, zmanjšan na:

θ = Ωt

V tem primeru se čas vrne na parametrične enačbe, kot so:

x = r.cos ωt

y = r. greh ωt

Vektorji enot Yo in J Zelo priročno so napisati funkcijo položaja predmeta r (T). Označujejo navodila na osi x in na osi in oziroma. Po njegovem mnenju je položaj delca, ki opisuje enakomerno krožno gibanje,:

r (t) = r.cos ωt Yo + R. greh ωt J

Rešene vaje

Vaja rešena 1

Top lahko ustreli kroglo s hitrostjo 200 m/s in kot 40 ° glede na vodoravno. Če se izstrelitev izvaja na ravnem terenu in je odpornost zraka zaničena, poiščite:

a) enačba usmeritve in (x) ..

b) parametrične enačbe x (t) in in (t).

c) Vodoravni doseg in čas, ki izstreli v zraku.

d) višina, na kateri se nahaja izstrel, ko je x = 12.000 m

Rešitev)

a) Za iskanje poti se nadomestijo vrednosti v enačbi y (x) prejšnjega odseka:

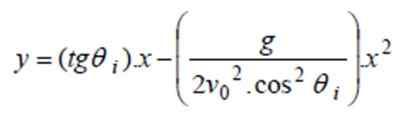
in (x) = tg 40 °. x - 9.8/(2 '400². cos²40 °) x² ⇒  in (x) = 0.8391 x - 0.0000522X²

Rešitev B)

b) Izhodiščna točka je izbrana pri izvoru koordinatnega sistema (0,0):

x (t) = x_tudi +v_vol.T = 400'Cos 40 °.T = 306.42. t.

in (t) = y_tudi +v_Oy.T -½g.t²= 400 'Sen 40 °.T - 0.5 '9.8t²= 257.12 T - 4.9.t²

Rešitev C)

c) Da bi našli čas, ki izstreli v zraku, je to storjeno in (t) = 0, Biti izstrelitev je narejena na ravnem terenu:

Vam lahko služi: kaj je relativno in absolutno hrapavost?

0 = 257.12.T - 4.9.t²

T = 257.12/4.9 S = 52.473 s

Vodoravni največji obseg nadomešča to vrednost v x (t):

x_Max = 306.42'52.47 M = 16077.7 m

Drug način za iskanje x_Max V enačbi usmeritve neposredno dela y = 0:

0 = 0.8391 x_Max - 0.0000522 x²_Max

x = 0.8391 /0.0000522 M = 16078.5m

Zaradi zaokroževanja decimalk je majhna razlika.

D) rešitev

D) Če želite vedeti višino, ko je x = 12000 m, se ta vrednost zamenja neposredno v enačbi poti:

in (12000) = 0.8391'12000 - 0.0000522'12000² M = 2552.4 m

Vaja Rešena 2

Funkcija položaja predmeta je podana z:

r (t) = 3T Yo + (4 -5T²) J m

Najti:

a) enačba za pot. Kaj je krivulja?

b) začetni položaj in položaj, ko je t = 2 s.

c) premik, narejen po t = 2 s.

Rešitev

a) Funkcija položaja je bila podana v smislu vektorjev enot Yo in J, ki določajo naslov na osi x in in, Zato:

x (t) = 3T

in (t) = 4 -5T²

Enačba poti in (x) Čisti se t od x (t) in zamenjava in (t):

T = x/3

in (x) = 4 -5. (x/3)² = 4 - 5x²/9 (prispodoba)

b) Začetni položaj je: r (2) = 4 J m ; Položaj v T = 2 s je r (2) = 6 Yo -16 J m

c) premik Dr Gre za odštevanje obeh položajev vektorjev:

Δr = r (2) - r (2) = 6 Yo -16 J- 4 J = 6 Yo - dvajset J m

Vaja rešena 3

Zemlja ima polmer r = 6300 km in znano je, da je obdobje vrtenja njegovega gibanja okoli njegove osi nekega dne. Najti:

a) Enačba poti točke na zemeljski površini in njegova položaj.

b) hitrost in pospeševanje omenjene točke.

Rešitev)

a) Funkcija položaja za katero koli točko v krožni orbiti je:

r (t) = r.cos ωt Yo + R.greh ωt J

Imate polmer zemlje r, ne pa tudi kotne hitrosti ω, vendar ga je mogoče izračunati iz obdobja, saj vemo, da za krožno gibanje velja, da reče:

Ω = 2π × Frekvenca = 2π / obdobje

Obdobje gibanja je: 1 dan = 24 ur = 1440 minut = 86400 sekund, torej:

Ω =  2π / 86400 s = 0.000023148 ​​s^-1

Zamenjava v funkciji položaja:

r (t) = r.cos ωt Yo + R. greh ωt J = 6300 (cos 0.000023148T Yo + greh 0.000023148T J) Km

Pot v parametrični obliki je:

x (t) = 6300. cos 0.000023148T

in (t) = 6300. greh 0.000023148T

Rešitev B)

b) Za krožno gibanje velikost linearne hitrosti v točke je povezano z kotno hitrostjo W skozi:

v = ΩR = 0.000023148 ​​s^-1'6300 km = 0.1458 km/s = 145.8 m/s

Celo stalno gibanje 145.8 m/s, Obstaja pospešek, ki kaže na središče krožne orbite, ki je odgovoren za ohranjanje točke v rotaciji. Je centripetalni pospešek do_c, dobiti od:

do_c = v² / R = (145.8 m/s)² / 6300 × 10³ M = 0.00337 m/s².

Reference

1. Giancoli, d. Fizika. (2006). Načela z aplikacijami. 6^th Dvorana Prentice. 22-25.
2. Kirkpatrick, l. 2007. Fizika: pogled na svet. 6^ta Skrajšana izdaja. Cengage učenje. 23 - 27.
3. Resnick, r. (1999). Fizično. Zvezek 1. Tretja izdaja v španščini. Mehika. Continental uredništvo s.Do. od c.V. 21-22.
4. Rex, a. (2011). Osnove fizike. Pearson. 33 - 36
5. Sears, Zemansky. (2016). Univerzitetna fizika s sodobno fiziko. 14^th. Ed. Zvezek1. 50 - 53.
6. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 1. 7^ma. Izdaja. Mehika. Uredniki učenja Cengage. 23-25.
7. Serway, r., Vulle, c. (2011). Osnove fizike. 9^na Ed. Cengage učenje. 43 - 55.
8. Wilson, J. (2011). Fizika 10. Pearson Education. 133 - 149.