Fourier diskretno preoblikovane lastnosti, aplikacije, primeri

The Fourier diskretno preoblikovan To je numerična metoda, ki se uporablja za opredelitev vzorcev, povezanih s spektralnimi frekvencami, ki sestavljajo signal. Študije periodične funkcije v zaprtih parametrih, kar je rezultat še en diskreten signal.

Da bi dobili diskretno transformacijo furierja iz N točk, na diskretnem signalu morata biti izpolnjena naslednja dva pogoja v zaporedju X [n]

 x [n] = 0   N n - 1

Če izpolnjujete te pogoje

TDF

Fourierjeva diskretna preobrazba je mogoče opredeliti kot vzorčenje na n točkah Fourierove transformacije.

[TOC]

Interpretacija Fourierjeve diskretne preobrazbe

Vir: Pexels

Obstajata dve stališču, iz katerih lahko razlagate rezultate, dobljene v zaporedju X_s[n] skozi Fourierovo diskretno preobrazbo.

-Prva ustreza spektralnim koeficientom, ki so že znani v seriji Fourier. Opazimo ga v diskretnih periodičnih signalih, pri čemer se vzorci sovpadajo z zaporedjem x_s[N].

-Drugi govori o spektru diskretnega aperiadnega signala, pri čemer vzorci ustrezajo zaporedju x_s[N].

Diskretna transformacija je pristop k spektru prvotnega analognega signala. Njegova faza je odvisna od trenutkov vzorčenja, medtem ko je njegova velikost odvisna od intervala vzorčenja.

Lastnosti

Algebrski temelji strukture predstavljajo logično osnovo naslednjih razdelkov.

Linearnost

C . S_n → c . F [S_k]; Če bo zaporedje pomnožilo skalarno, bo tudi njegova preobrazba.

T_n + V_n = F [t_k]+F [v_k]; Preobrazba vsote je enaka vsoti preoblikovanih.

Dvojnost

F [s_n] → (1/n) s_-K; Če se diskretna transformacija Fourierja odpokliče na izraz, ki je že preoblikovan, dobimo isti izraz, ki se pleza v N obrnjenem glede na navpično osi.

Shranjevanje

Preganjanje podobnih ciljev, ki se v Laplace Transform nanašajo na izdelek med njegovimi Fourierovimi transformacijami. Convolution velja tudi za diskretne čase in je odgovoren za številne sodobne postopke.

X_n * R_n → F [x_n] .F [r_n]; Preoblikovanje zvijanja je enaka produktu tistih, ki se preoblikujejo.

X_n . R_n→ F [x_n] * F [r_n]; Preobrazba izdelka je enaka konvoluciji preoblikovanih.

Premik

X_N-m → F [x_k] e ^{-I (2π/n) km} ; Če se nasledstvo zavleče v vzorcih M, bo njegov vpliv na diskretno preobrazbo sprememba kot, ki ga določa (2π/n).

Vam lahko služi: Zakaj je algebra pomembna v določenih vsakdanjem življenju?

Simetrija konjugirano

X_t [-K] = x*_t[k] = x_t [N - k]

Modulacija

W^-nm_N . x [n] ↔ x_t[K - M]

Izdelek

x [n] y [n] ↔ (1/n) x_t[K]*in_t[K]

Simetrija

X [-n] ↔ x_t[-K] = x*_t[K]

Konjugat

x*[n] ↔ x*_t[-K]

Parseval enačba 

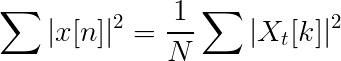
Podobnosti in razlike s Fourierovo preobrazbo

Glede na konvencionalno preobrazbo Fourierja ima več podobnosti in razlik. Fourierjeva transformacija pretvori zaporedje v neprekinjeno črto. Na ta način se reče, da je rezultat Fourierjeve spremenljivke zapletena realna spremenljivka.

Fourierjeva diskretna transformacija, za razliko od tega, prejme diskreten signal in ga spremeni v drug diskreten znak, to je zaporedje.

Kakšna je uporaba Fourierjeve diskretne preobrazbe?

V glavnem služijo pomembnim enačbam, medtem ko preoblikovanje izrazov izhaja v elemente moči. Označevanje diferencialnih izrazov v oblikah integriranih polinomov.

Pri optimizaciji, modulaciji in modeliranju rezultatov deluje kot standardiziran izraz, ki je pogost vir za inženiring po več generacijah.

Vir: Pixabay

Zgodovina

Ta matematični koncept je predstavil Joseph B. Fourier leta 1811, medtem ko je razvijal pogodbo o Toplota. Hitro so ga sprejele različne veje znanosti in inženiringa.

Ustanovljeno je bilo kot glavno delovno orodje pri preučevanju enačb z delnimi derivati, v primerjavi celo z delovnim odnosom med Laplace transformirane in navadne diferencialne enačbe.

Vsaka funkcija, ki jo je mogoče opraviti s Fourierovo preobrazbo.

Fourier diskretno preoblikovan in inverzno

Diskretna transformacija dobimo z izrazom:

Po diskretnem zaporedju x [n]

Inverzna Fourierjeva diskretna preobrazba je definirana z izrazom:

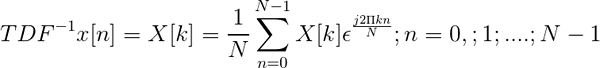Inverzni TDF

Omogoča, ko se diskretno preoblikuje, določite zaporedje v časovni domeni x [n].

Fino

Postopek parametrizacije, ki ustreza Fourierjevi diskretni preobrazbi, je v mladiču. Za delo preoblikovanje moramo pravočasno omejiti zaporedje. V mnogih primerih zadevni signali nimajo teh omejitev.

Nasledek, ki ne izpolnjuje meril velikosti, ki bi se nanašalo na diskretno preobrazbo, je mogoče pomnožiti s funkcijo "okna" V [n], ki določa vedenje nasledstva v nadzorovanem parametru.

Vam lahko služi: krožne permutacije: demonstracije, primeri, rešene vaje

X [n] . V [n]

Širina spektra bo odvisna od širine oken. Ko se širina okna povečuje, bo izračunani preoblikovani ožji.

Prijave

Izračun temeljne rešitve

Fourierjeva diskretna preobrazba je močno orodje pri preučevanju diskretnih nasledstva.

Fourierjeva diskretna transformacija spremeni funkcijo neprekinjene spremenljivke v diskretno spremenljivo transformacijo.

Cauchyeva težava za toplotno enačbo predstavlja pogosto polje uporabe Fourierove diskretne transformacije. Kjer se ustvari funkcija Dirichlet toplota ali jedro, ki velja za vrednosti vzorčenja v določenem parametru.

Teorija signala

Splošni razlog za uporabo Fourierove diskretne preobrazbe v tej veji je večinoma posledica značilne razgradnje signala kot neskončnega prekrivanja lažje obdelanih signalov.

To je lahko zvočni val ali elektromagnetni val, Fourierjeva diskretna transformacija ga izraža v preprostem prekrivanju valov. Ta predstavitev je precej pogosta pri elektrotehniki.

Fourierjeva serija

So opredeljene serije v smislu Cosenosa in dojk. Služijo za lažje delo s splošnimi periodičnimi funkcijami. Ko se uporabljajo, so del tehnik ločljivosti delnih in običajnih diferencialnih enačb.

Serije Fourier so še bolj splošne od Taylorjeve serije, saj razvijajo periodične funkcije prekinitve, ki v seriji Taylor nimajo zastopanosti.

Druge oblike serije Fourier

Za analitično razumevanje Fourierjeve preobrazbe je pomembno.

-Fourierjeva serija na funkciji 2L obdobja:

Velikokrat je treba prilagoditi strukturo Fourierjeve serije, na periodične funkcije, katerih obdobje je p = 2l> 0 v intervalu [-l, l].

-Fourierjeva serija v enakomernih in nenavadnih funkcijah

Upošteva se interval [-π, π], ki ponuja prednosti pri izkoriščanju simetričnih značilnosti funkcij.

Vam lahko služi: končni niz: lastnosti, primeri, rešene vaje

Če je F navor, je serija Fourier vzpostavljena kot serija Cosenosa.

Če je f čuden, je serija Fourierjeva ustanovljena kot niz prsi.

-Kompleksni zapis serije Fourierja

Če imate funkcijo f (t), ki izpolnjuje vse zahteve serije Fourier, jo je mogoče označiti v intervalu [-t, t] z uporabo njene zapletene zapise: 

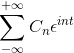
Primeri

Glede izračuna temeljne rešitve so predstavljeni naslednji primeri:

Laplace enačba

Enačba toplote

Schrödingerjeva enačba

Valovna enačba

Po drugi strani obstajajo primeri uporabe Fourierove diskretne preobrazbe na področju teorije signala:

-Težave z identifikacijo sistema. Ustanovljena F in G

-Težava s konsistenco izhodnega signala

-Težave s filtriranjem signala

Vaje

Vaja 1

Izračunajte Fourierovo diskretno preobrazbo za naslednje naslednjo naslednjo.

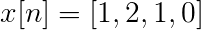
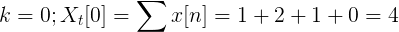
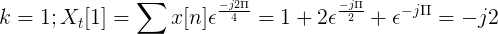
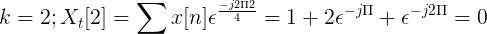
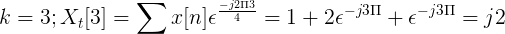
TDF x [n] lahko definiramo kot:

X_t[k] = 4, -j2, 0, j2 za k = 0, 1, 2, 3

Vaja 2

S pomočjo digitalnega algoritma ga želi določiti spektralni signal, ki ga definira izraz x (t) = e^-t. Kjer je koeficient zahteve največje frekvence f_m= 1Hz. Harmonika ustreza F = 0.3 Hz. Napaka je omejena na manj kot 5%. Izračunati F_s , D in n.

Ob upoštevanju teorema vzorčenja F_s = 2f_m = 2 Hz

Frekvenčna ločljivost F₀ = 0.1 Hz, kjer je D = 1/0,1 = 10s

0.3 Hz je frekvenca, ki ustreza indeksu k = 3, kjer je n = 3 × 8 = 24 vzorcev. Kar kaže na to F_s = N/d = 24/10 = 2.4> 2

Ker je namen doseči najmanj možno vrednost za n, se lahko naslednje vrednosti obravnava kot rešitev:

F₀ = 0.3 Hz

D = 1/0.3 = 3.33S

K = 1

N = 1 × 8 = 8

Reference

1. Obvladovanje diskretne Fourierjeve preobrazbe v eni, dveh ali več dimenzijah: pasti in artefaktov. Isaac Amidor. Springer Science & Business Media, 19. julij. 2013
2. DFT: Priročnik lastnikov za diskretno Fourierovo preobrazbo. William l. Briggs, Van Emden Henson. Siam, 1. januar. Devetnajst devetdeset pet
3. Digitalna obdelava signalov: teorija in praksa. D. Sundararajan. World Scientific, 2003
4. Transformacije in hitri algoritmi za analizo in reprezentacije signala. Guoan Bi, Yonghong Zeng. Springer Science & Business Media, 6. december. 2012
5. Diskretne in neprekinjene Fourierjeve preobrazbe: analiza, aplikacije in hitri algoritmi. Eleanor Chu. CRC Press, 19. 2008