Lastnosti linearnih transformacij, kakšne so uporaba, vrste, primeri

A Linearna transformacija, ki ga bomo preprosto poklicali, poveže elemente dveh vektorskih presledkov V in W in dodeli vsak vektor v pripada V enemu vektorju W ki pripada W, skozi določeno operacijo.

Ta preobrazba izpolnjuje dva pogoja:

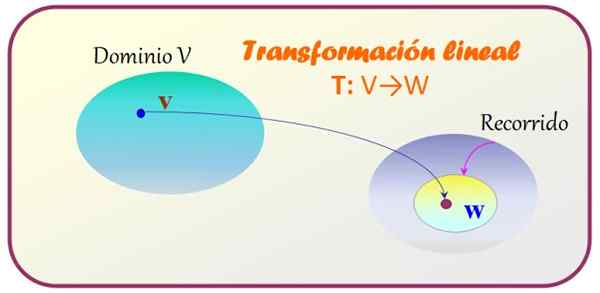
Slika 1. Linearna transformacija velja za vektor vektorskega prostora V, da dobimo še en vektor, ki pripada vektorskemu prostoru. Vir: f. Zapata.

-Pogoj 1

Nanaša se na dodatek, tako da je treba izpolniti t -linearno transformacijo, ki:

T (v + W) = T (v) + T (W)

-Pogoj 2

Drugi pogoj predstavlja homogenost pri množenju skalarja z vektorjem:

T (cv) = c⋅t (v)

Linearna transformacija, kot že ime pove, je odgovorna za preslikavo ali preoblikovanje elementov V v elemente W.

Zapis za funkcije se uporablja tudi v primeru linearnih transformacij, zato je domena V nabor elementov (vektorjev), ki jih je treba preoblikovati, medtem ko je kodominij ali pot dobljeni niz.

Primer linearne preobrazbe je:

Da bi navedli, da bo črka T uporabljena. Preobrazba bo uporabljena za vektor v katerih komponente sta x in y, ki je bila predstavljena z eno samo matrico stolpca. Rezultat je še en vektor W katerih komponenta sta x in 0, predstavljena pa tudi z matrico stolpca.

Zato je to preobrazba R vektorskega prostora R² Proti vektorskemu prostoru r², Če povzamemo, je napisano tako:

T: r² → R²         

Če imamo vektor:

Preobrazba nas vrne:

In tako s katerim koli r vektorjem². V primeru 1 bo preverjeno, da je ta preobrazba linearna.

[TOC]

Lastnosti linearnih transformacij

Recimo linearna transformacija V v W, v kateri vektorji v in ali Pripadajo V, potem so izpolnjene naslednje lastnosti:

Lastnina 1

T (0) = 0

Kje 0 je ničelni vektor.

Lastnina 2

T (-v) = - t (v)

Lastnina 3

T (ali  - v) = T (ali) - t (v)

Lastnina 4

Biti v = c₁v₁ + c₂v₂ +.. . +  c_nv_n

 Tako:

T (c₁v₁ + c₂v₂ +.. . +  c_nv_n) = c₁ T (v₁) + c₂ T (v₂) +.. . +  c_n T (v_n)

Elementi linearne transformacije

Naj V in W že omenita vektorske prostore, kjer linearna transformacija t preoblikuje elemente V v W. Lahko določimo naslednje elemente:

-C jedro ali jedro: Je podskupina domene, ki jo označuje N (t) tudi ker (t) in razumeti vse elemente V, tako da:

T (v) = 0.

Linearna transformacija t (v) = 0 je poklican ničelna preobrazba.

Seveda ničelni vektor v = 0 Vseeno izpolnjuje s tem pogojem, vendar jedro sestavljajo celotni vektorji, ki niso vnul, ki ga prav tako izpolnjujejo, za dano t.

Lahko vam služi: Graščanje funkcije: Kako jo prepoznati, primeri, vaje

-Slika T: To je nabor vektorjev, ki pripadajo W, ki so podoba vsaj nekega vektorja v V. Označeno je kot Im t) In je podmnožica vektorskega prostora.

Ti elementi nam bodo pomagali pozneje razvrstiti linearne preobrazbe.

Za kaj so linearne transformacije?

Sprva linearne transformacije delujejo z vektorskimi prostori, ki jih tvorijo vektorji. Večkrat vektorje povezujemo z močjo in drugimi fizičnimi velikostmi, vendar lahko pri digitalni obdelavi slik piksel predstavlja vektor.

V tem primeru lahko sliko manipuliramo s priročnimi linearnimi transformacijami, da dobimo želene učinke, na primer projiciranje, vrtenje, iskanje zrcalne slike ali spreminjanje njegove velikosti, ne da bi spremenili relativne dimenzije.

Linearne transformacije se pogosto uporabljajo tudi v ekonomiji in odločanju, na primer, da vemo, koliko surovin, potrebnih za izdelavo določene serije izdelkov.

Število kosov, potrebnih za sestavljanje različnih modelov, ki jih proizvaja tovarna, je mogoče delati z matrično ureditvijo, kot bomo videli kasneje.

Vrste linearnih transformacij (razvrstitev)

Tako kot funkcije so lahko tudi linearne transformacije:

-Injektivno ali Monomorfizmi

-Bijekti ali Epimorfizmi

-Pretirano ali Izomorfizmi

Poleg tega so naslednje vrste:

-Endomorfizmi

-Avtomatizmi.

Injektivne linearne transformacije

Naj V in W vektorski presledki in t linearna transformacija T: V → W. T je injektiven, ko:

Ker (T) = 0

Linearne prekomerne transformacije

Če sta V in W vektorska prostora, tako da je T: V → W, je rečeno, da je T Bijective, ko:

Im (t) = w

Bijjektivne linearne transformacije

Linearna transformacija T: V → W je bijektivna, ko je tako injektivna in pretirana. Zato je izpolnjeno:

Ker (T) = 0 in Im (t) = w

Endomorfizmi

Gre za linearne transformacije, v katerih domena in kodominium sovpadata.

Avtomatizmi

Tovrstne linearne transformacije so bijektivni endomorfizmi.

Posebne linearne preobrazbe

Linearni operater

Linearna transformacija T: V → V, ki sega iz vektorskega prostora v isti vektorski prostor, se imenuje Linearni operater.

Ničelna preobrazba

Zgoraj omenjeno, nič transformacija je pomembna za iskanje jedra linearne transformacije:

Lahko vam služi: tetrademágon

T: v → w takšen, da je t (v) = 0 Za katero koli v.

Preobrazba identitete

T: v → v tako, da je t (v) = v  Za katero koli v.

Preobrazba, ki jo definira matrica

T: v → w takšen, da je t (v) = Av, kjer je a matrica in v To je vektor stolpca.

Linealna funkcija

Linearne funkcije tipa y = mx so linearne transformacije. Vzemimo za primer y = 3x in preverite, ali izpolnjuje dva pogoja začetka, testirate z dvema vrednostima A in B

F (A+B) = 3 (A+B) = 3A+3B = F (A)+F (B)

f (ka) = 3 (ka) = k⋅ (3a) = k⋅f (a)

Dejansko gre za linearno preobrazbo.

Prijave

Linearne transformacije imajo matematične aplikacije, kot so:

-Koordinirane vrtenje osi.

-V rešitvi sistemov linearnih diferencialnih enačb.

-Težave z vrednostjo in samodejnim prevozom.

In imajo tudi aplikacije na drugih področjih znanosti, na primer v mehaniki, kvantni mehaniki in gospodarstvu, med drugim.

Primeri linearnih transformacij

Primer 1

V mnogih težavah z mehaniko moramo najti projekcijo vektorja v pripada vesolju, na določeni ravnini. Ta vektor v lahko na primer predstavlja silo.

Recimo, da želite projicirati vektor v = Na ravnini xy. Lahko določimo linearno transformacijo, ki jo daje naslednja matrika:

Ko ga nanesemo na vektor v Dobimo vektorja, katerega z komponento je preklicana. Geometrijsko je predstavljen s projekcijo v Na ravnini xy kot rdeči vektor z dvema komponentama.

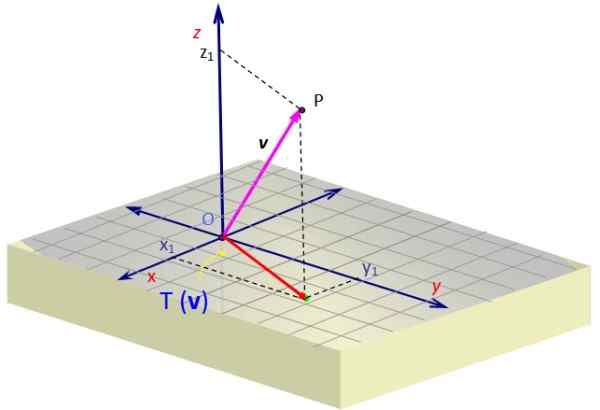Slika 2. Projekcija vektorja v vesolju na ravnini, ki jo dobimo z linearno transformacijo. Vir: f. Zapata.

Primer 2

Recimo, da imate tovarno, ki proizvaja tri vrste vozičkov za igrače: C1, C2 in C3, za katere v določenih količinah potrebujete tri vrste kosov za izdelavo vsake vrste vozička:

-Osi ali kos

-Kolesa ali kos B

-Podvozje ali kos c

Za vsako vrsto vozička je število kosov drugačno, saj so modeli različni. Zneske lahko sprejmemo v matriki 3 × 3, v kateri stolpci vodijo vrsto vozička, in vrsta.

To je primer preobrazbe, ki jo daje matrika, ki bi bila takšna:

Če tovarna prejme določeno naročilo, ki ga sestavlja x količina C1, in  od C2 in z Od C3, koliko kosov A, B in C mora imeti na voljo za sestavljanje vozičkov?

Lahko vam služi: kaj so algebrski izrazi in ki so najpogostejši?

Najti moramo linearno transformacijo T (x), tako da:

Da dobim vektor in:

To nam bo dalo količino delov, ki jih moramo imeti pri na razpolago. V letu razrešeno 2 ocenjujemo učinkovitost linearnih preobrazb, da bi našli količino delov, potrebnih za izpolnitev določenega naročila.

Rešene vaje

- Vaja 1

Preverite, ali naslednja preobrazba T: r² → R² Je linearno:

Rešitev

Če želite to narediti, morate zagotoviti, da preobrazba izpolnjuje dva pogoja, opisana na začetku, najprej dodajanje in nato produkt skalar za vektor. Torej morate vzeti dva vektorja v in  ali pripada r², Pisanje z matrico zapisovanje ali določitev komponent.

Ti vektorji so:

v = x₁, in₁

ali = x₂, in₂

Prvi pogoj

-Če spomnimo, da so vektorji dodani komponenta, je treba preveriti, da:

T (v+ali) = T (v) + T (ali)

T (v+ali) = T (x₁+ x₂ ; in₁ + in₂)

Od tu je pridobljeno:

T (x₁+ x₂ ; in₁ + in₂) = (x₁+ x₂; 0

-Po drugi strani pa pri uporabi transformacije na vsak vektor ločeno:

T (x₁,in₁) + T (x₂,in₂) = (x₁,0) + (x₂,0

Z dodajanjem nastalih vektorjev je učinkovito dosežen:

W = (X₁+ x₂; 0

Ker sta oba rezultata enaka, je prvi pogoj izpolnjen.

Drugi pogoj

Zdaj bomo preverili, da lahko s pomnoževanjem s sklenerjem C lahko izstopi iz preobrazbe:

T (cv) = c⋅t (v)

Sean:

v = x₁, in₁

c.v = C⋅x₁, C⋅y₁

Tako:

T (cv) = T (c⋅x₁, C⋅y₁ ) = (C⋅x₁ , 0

Toda to vemo iz prejšnjega koraka, da je t (v) = T (x₁, in₁ ) = (X₁ , 0.

Ker sta oba izraza enaka, je izpolnjen tudi drugi pogoj in transformacija je linearna.

- Vaja 2

Tovarna igračka sestavlja tri modele vozil: C1, C2 in C3, za katere potrebujete koščke A, B in C, ki so ozi, kolesa in podvozje. Zahtevani zneski so v naslednji tabeli:

Tovarna je bila pozvana, naj pripravi 12 modelov C1, 22 C2 in 16 C3. Koliko kosov A, B in C je potrebno za dokončanje naročila?

Rešitev

Uporablja se linearna transformacija T (x) = y, katere rezultat je izdelek med matricami:

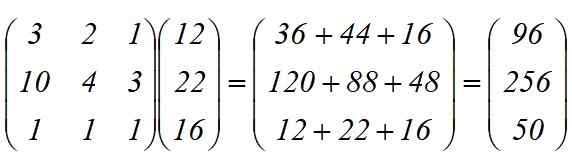
Skupno so potrebne:

-96 osi

-256 koles

-50 podvozja.

Reference

1. Algebra in analitična geometrija. Jedro in podoba. Razvrstitev linearnih preobrazb. Okreval od: aga.frba.UTN.Edu.ar.
2. Grossman, s. 2012. Linearna algebra. 7. Izdaja. McGraw Hill.
3. Gutiérrez, e. 2014. Linearna algebra in njegove aplikacije. Uredniška skupina Patria.
4. Larson, r. 2016. Osnove linearne algebre. 6. Izdaja. Cengage učenje.
5. Wikipedija. Linearne aplikacije. Okrevano od: je.Wikipedija.org.