Mehansko delo, kar je, pogoji, primeri, vaje

On Mehansko delo Opredeljen je kot sprememba energetskega stanja sistema, ki jo povzroča delovanje zunanjih sil, kot sta gravitacija ali trenje. Mehanske delovne enote v mednarodnem sistemu (SI) so Newton X Metro ali Joules, okrajšano J.

Matematično je opredeljen kot skalarni produkt sile sile z vektorskim premikom. Ja F To je stalna sila in l To je premik, oba vektorja, delo w je izraženo kot: W = F ● l

Slika 1. Medtem ko športnik dviguje težo, deluje proti gravitaciji, ko pa teže vzdržuje negibno, z vidika fizike ne dela. Vir: Needpix.com

Kadar sila ni konstantna, moramo analizirati opravljeno delo, ko so premiki zelo majhni ali diferenčni. V tem primeru, če se šteje za izhodišče do točke A in kot prihod na B, se skupno delo dobi z dodajanjem vseh prispevkov v isto. To je enakovredno izračunu naslednjega integrala:

In kot je navedeno na začetku, pod pogojem, da pride do spremembe v sistemski energiji, bo to zato, ker obstajajo sile iz tujine, ki delujejo nanjo:

Nihanje v sistemski energiji = delo, ki jo izvajajo zunanje sile

ΔE = w_ext

Ko se sistemu doda energija, w> 0 in ko ga odštejemo<0. Ahora bien, si ΔE = 0, puede significar que:

-Sistem je izoliran in nanj ni zunanjih sil.

-Obstajajo zunanje sile, vendar ne delajo na sistemu.

Ker je nihanje energije enakovredno delu, ki ga opravijo zunanje sile, enota, če je energija tudi Joule. To vključuje katero koli vrsto energije: kinetična, potencialna, toplotna, kemična in še več.

[TOC]

Pogoji, da obstajajo mehansko delo

Že smo videli, da je delo opredeljeno kot skalarni izdelek. Vzemimo definicijo dela s stalno silo in uporabimo koncept skalarnega izdelka med dvema vektorjema:

W = F ● L = F.l.cos θ

Kje F To je velikost sile, l To je velikost premika in θ Je kot, ki obstaja med silo in premikom. Na sliki 2 je primer nagnjene zunanje sile, ki deluje na blok (sistem), ki proizvaja vodoravni premik.

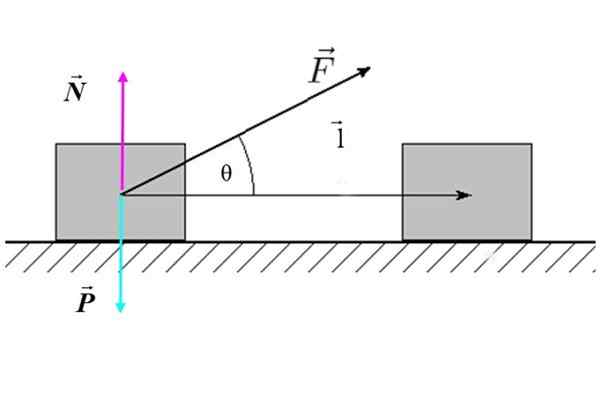Slika 2. Prosti karoserijski diagram bloka, ki se premika na ravni površini. Vir: f. Zapata.

Prepisovanje dela na naslednji način:

W = (f. cos θ). l

Lahko potrdimo, da je samo komponenta sile vzporedna z premikom: F. cos θ es sposoben delati. Če je θ = 90 °, potem cos θ = 0 in delo bi bilo nično.

Zato je sklenjeno, da sile pravokotne do premika ne opravljajo mehanskega dela.

V primeru slike 2, niti normalne sile N niti teža Str Delujejo, ker sta oba pravokotna na premik l.

Znaki dela

Kot je razloženo zgoraj, W Lahko je pozitiven ali negativen. Ko cos θ> 0, Delo, opravljeno s silo, je pozitivno, saj ima enako smer gibanja.

Lahko vam služi: masna številka: kaj je to in kako ga dobiti (s primeri)

Ja cos θ = 1, Moč in premik sta vzporedna in delo je največ.

V primeru cos θ < 1, la fuerza no está a favor del movimiento y el trabajo es negativo.

Kdaj cos θ = -1, Sila je popolnoma nasprotna premiku, kot je kinetično trenje, katere učinek je ustaviti predmet, na katerem deluje. Torej je delo minimalno.

To se strinja s tistim, kar je bilo rečeno na začetku: če je delo pozitivno, se sistem dodaja energija, in če je negativno, se odšteje.

Neto delo W_mreža Opredeljen je kot vsota del, ki jih izvajajo vse sile, ki delujejo na sistem:

W_mreža = ∑W_Yo

Nato lahko sklepamo, da je za zagotovitev obstoja neto mehanskega dela potrebno:

-Zunanje sile delujejo na predmet.

-Te sile niso pravokotne na premik (cos θ ≠ 0).

-Dela, ki jih opravi vsaka sila, se med seboj ne prekličejo.

-Obstaja premik.

Mehanski primeri dela

-Kadar koli je treba objekt sprožiti v gibanju na podlagi počitka, je treba opraviti mehansko delo. Na primer potisnite hladilnik ali težko prtljažnik na vodoravno površino.

-Drug primer situacije, v kateri je treba opraviti mehansko delo, je spremeniti hitrost premikajoče se kroglice.

-Za dvigovanje predmeta na določeni višini je treba delati na tleh.

Zdaj obstajajo enako pogoste situacije, v katerih Ne Delo je opravljeno, čeprav nastopi kažejo drugače. Rekli smo, da moramo za dvig predmeta na določeni višini, zato moramo delati, zato naložimo predmet, ga dvignemo nad glavo in ga obdržamo tam. Ali delamo?

Očitno da, ker če je predmet težak, se bodo roke kmalu naveličale, ne glede na to, koliko dela je opravljeno, delo ne opravlja z vidika fizike. Zakaj ne? Ker se predmet ne premika.

Drug primer, v katerem je, kljub zunanji sili, ne opravlja mehanskega dela, ko ima delček enakomerno krožno gibanje.

Lahko vam služi: normalen napor: iz česa je sestavljen, kako se izračuna, primeri

Na primer otrok, ki obrne kamen, privezan na vrvico. Napetost vrvice je centripetalna sila, ki omogoča vrtenje kamna. Toda ta sila je ves čas pravokotna na premik. Potem ne opravljajte mehanskega dela, kljub temu, da je naklonjen gibanju.

Cinetika teorema delovne energije

Kinetična energija sistema je tisto, kar ima pod svojim gibanjem. Ja m je testo in v To je hitrost gibanja, kinetična energija pa označuje K In daje ga:

K = ½ mV²

Po definiciji kinetična energija predmeta ne more biti negativna, saj sta tako masa kot kvadrat hitrosti vedno pozitivna količina. Kinetična energija je lahko 0, ko objekt v mirovanju.

Za spremembo kinetične energije sistema je potrebno-. Za to je treba opraviti neto delo na sistemu:

W_mreža = ΔK

To je teorem o delu - kinetična energija. Navaja, da:

Neto delo je enakovredno spremembi kinetične energije sistema

Upoštevajte, da čeprav je K vedno pozitiven, je ΔK lahko pozitiven ali negativen, saj:

Δk = k_finale - K _začetno

Ja K_finale >K _začetno Sistem je pridobil energijo in Δk> 0. Nasprotno, da K_finale < K _začetno, Sistem je dal energijo.

Delo, opravljeno za raztezanje pomladi

Pri raztezanju (ali stiskanju) vzmeti je potrebno opraviti delo. To delo je shranjeno spomladi, kar omogoča, da to stori, recimo, blok, ki je pritrjen na enega od njegovih koncev.

Hookov zakon navaja, da je sila, ki jo ima pomlad, restitucijska sila - v nasprotju s premikom - in tudi sorazmerno z omenjenim premikom. Konstanta sorazmernosti je odvisna od tega, kako je vzmet: mehka in enostavno deformabilna ali toga.

To silo daje:

F_r = -kx

V izrazu, F_r To je sila, k To je vzmetna konstanta in x To je premik. Negativni znak kaže, da sila, ki jo ima vzmet, nasprotuje premiku.

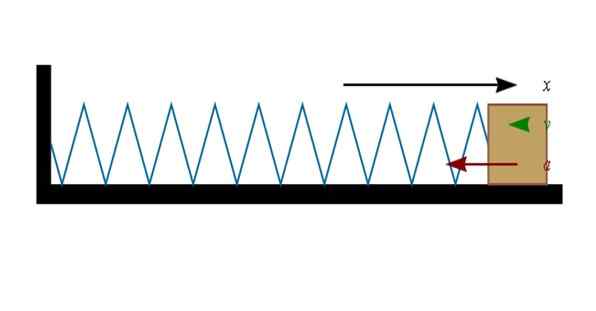Slika 3. Stisnjena ali raztegnjena vzmet deluje na predmetu, vezanem na svoj konec. Vir: Wikimedia Commons.

Če je vzmet stisnjena (levo na sliki), se bo blok na koncu premaknil v desno. In ko se vzmet raztegne (desno), se bo blok želel premakniti v levo.

Za stiskanje ali raztezanje vzmeti mora nekaj zunanjega agenta opraviti nalogo, in ker je spremenljiva sila, za izračun tega dela morate uporabiti definicijo, ki se je zgodila na začetku:

Vam lahko služi: Darcy Law

Zelo pomembno je opozoriti, da je to delo, ki ga opravi zunanji agent (na primer roka osebe), da se vzmet stisne ali raztegne. Zato se negativni znak ne pojavi. In ker so položaji kvadratni, ne glede na to, ali gre za stiske ali raztezanje.

Delo, ki bo pomlad opravilo po vrsti blok, je:

W_pomlad = -W_ext

Vaje

Vaja 1

Blok na sliki 4 ima maso M = 2 kg in zdrsne skozi nagnjeno ravnino brez trenja, z α = 36.9. Ob predpostavki, da je dovoljeno, da z vrha ravnine zdrsne od ostalega, katere višina je H = 3 m, poiščite hitrost, s katero blok doseže osnovo ravnine, skozi kinetično delovno-energijsko energijo.

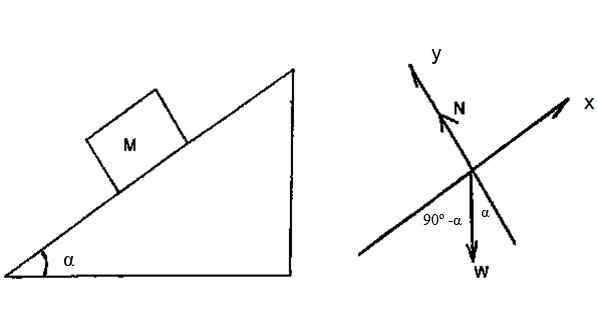Slika 4. Blok drsi navzdol na nagnjeni ravnini brez drgnjenja. Vir: f. Zapata.

Rešitev

Shema prostega telesa kaže, da je edina sila, ki je sposobna delati na bloku. Natančnejša: komponenta teže vzdolž osi x.

Razdalja, ki jo prevozi blok na ravnini, se izračuna s trigonometrijo:

D = 3 / (cos 36.9 °) M = 3.75 m

W_utež = (Mg). d. cos (90-α) = 2 x 9.8 x 3.75 x cos 53.1. j = 44.1 j

Z delovnim teoremsko-energijskim kinetikom:

W_mreža = ΔK

W_mreža = W_utež

ΔK = ½ mV_F²- ½ mV_tudi²

Ker je izdana iz počitka, v_tudi = 0, Zato:

W_mreža = ½ mV_F²

Vaja 2

Vodoravno vzmet, katere konstanta je k = 750 n/m je pritrjena za en konec na steno. Ena oseba stisne drugi konec na razdalji 5 cm. Izračunajte: a) Sila, ki jo je izvajala oseba, b) delo, ki ga je naredil za stiskanje vzmeti.

Rešitev

a) Obseg sile, ki jo uporablja oseba, je:

F = kx = 750 n/ m . 5 x 10 ^-2 M = 37.5 n.

b) Če je spomladanski konec prvotno v x₁ = 0, da ga odpeljete od tam do končnega položaja x₂ = 5 cm, v skladu z rezultatom, pridobljenim v prejšnjem razdelku, je treba opraviti naslednje delo:

W_ext = ½ K (x₂² - x₁²) = 0.5 x 750 x (0.05² -0²) J = 0.9375 J.

Reference

1. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 2. Dinamično. Uredil Douglas Figueroa (USB).
2. Iparraguirre, l. 2009. Osnovna mehanika. Zbirka in matematika naravoslovja. Brezplačna spletna distribucija.
3. Vitez, r. 2017. Fizika za znanstvenike in inženiring: strateški pristop. Pearson.
4. Fizika librettexts. Teorem o delovni energiji. Okrevano od: Phys.Librettexts.org
5. Delo in energija. Okrevano od: fizike.Bu.Edu
6. Delo, energija in moč. Okrevano od: ncert.Nic.v