Oblačne značilnosti paraboličnega posnetka, formule, enačbe, primeri

On Obložen parabolični strel To je poseben primer gibanja prostega padca, v katerem začetna hitrost izstrelkov tvori določen kot z vodoravno, kar ima za posledico parabolično pot.

Prosti padec je primer gibanja s stalnim pospeševanjem, v katerem je pospeševanje gravitacije, ki vedno kaže navpično navzdol in ima velikost 9,8 m/s^2. Ni odvisno od testa iz projektila, kot je dokazal Galileo Galilei leta 1604.

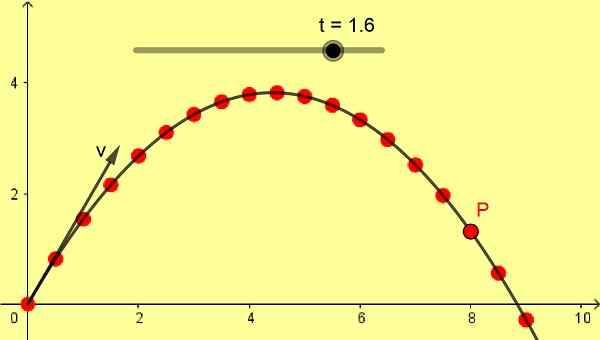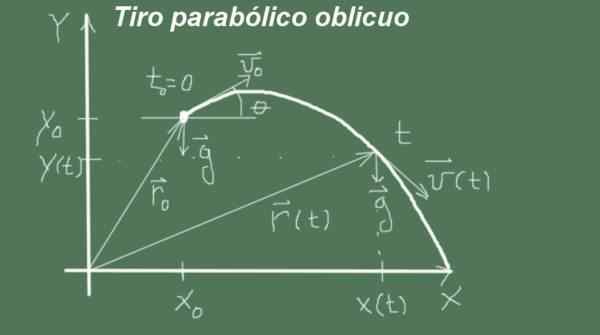
Slika 1. Obložen parabolični strel. (Lastna izdelava)

Če je začetna hitrost projektila navpična, ima prosti padec ravno in navpično usmeritev, če pa je začetna hitrost poševna, je usmeritev prostega padca parabolična krivulja, ki jo dokazuje tudi Galileo.

Primeri paraboličnega gibanja so usmeritev, ki sledi baseballu, krogla, ki jo izstreli top in vodni curek, ki izhaja iz cevi.

Slika 1 prikazuje poševen parabolični posnetek 10 m/s s kotom 60 °. Lestvica je v metrih, zaporedni P pa so opravljeni z razliko 0,1 s, ki se začne od začetnega trenutka 0 sekund.

[TOC]

Formule

Gibanje delca je v celoti opisano, če je znan njegov položaj, njena hitrost in pospešek kot funkcija časa.

Parabolično gibanje, ki je posledica poševnega posnetka.

Formule, ki veljajo za poševni parabolični posnetek, so tiste, ki ustrezajo gibanju s stalnim pospeševanjem a = g, Upoštevajte, da je bil Bold uporabljen za označevanje, da je pospešek vektorski znesek.

Vam lahko služi: naravni sateliti

Položaj in hitrost 

V konstantnem pospeševalnem gibanju je položaj matematično odvisen od časa na kvadraten način.

Če označujemo r(T) Položaj do časa t, rtudi Začetni takojšen položaj, vtudi Začetna hitrost, g pospešek in t = 0 Kot začetni trenutek formula, ki daje položaj za vsak trenutek t je:

r(t) = r_tudi + v_tudi T + ½ g t²

Krepko v prejšnjem izrazu kaže, da gre za vektorsko enačbo.

Hitrost kot funkcija časa dobimo z odvzemom derivata glede na t položaja in rezultat je:

v(t) = v_tudi + g t

In za pridobitev pospeška kot funkcije časa, hitrost, ki izhaja iz t rezultat:

do(t) = g

Ko čas ni na voljo, obstaja razmerje med hitrostjo in položajem, ki ga daje:

v² = vtudi² - 2 g (in - jaz)

Enačbe

Nato bomo našli enačbe, ki veljajo za poševni parabolični posnetek v kartezijanski obliki.

Slika 2. Spremenljivke in parametri poševnega paraboličnega posnetka. (Lastna izdelava)

Gibanje se trenutno začne t = 0 Z začetnim položajem (Xo, jaz) in hitrost magnitude vtudi in kot θ, to pomeni, da je začetni vektor hitrosti (vtudi cosθ, vtudi Senθ). Gibanje prehaja s pospeševanjem 

g = (0, -g).

Parametrične enačbe

Če se vektorska formula, ki daje položaj kot funkcija časa, uporabimo in komponente razvrstimo in izenačimo, bodo enačbe, ki jih koordinate položaja, dosežene v času, pridobiti.

x (t) = x_tudi + v_vol t 

in (t) = y_tudi + v_Oy t -½ g t²

Podobno so enačbe za komponente hitrosti kot časovna funkcija.

Lahko vam služi: normalen napor: iz česa je sestavljen, kako se izračuna, primeri

v_x(t) = v_vol

v_in(t) = v_Oy - g t 

Kje: v_vol = vtudi cosθ; v_Oy = vtudi Senθ

Enačba usmeritve

y = a x^2 + b x + c

A = -g/(2 Vvol^2)

B = (vOy/vvol + g xtudi/vvol^2)

C = (intudi - vOy xtudi / vvol)

Primeri 

Primer 1

Odgovorite na naslednja vprašanja:

a) Zakaj v težavah s paraboličnim streljanjem običajno prezira učinek trenja z zrakom?

b) oblikuje obliko predmeta v paraboličnem posnetku?

Odgovori

a) Da bi bilo gibanje izstrelkov parabolično, je pomembno, da je sila trenja zraka precej nižja od teže objekta. 

Če je vržena plutalna kroglica ali nekaj lahkega materiala, je sila trenja primerljiva s težo in njegova usmeritev se ne more približati paraboli.

Nasprotno, če je težek predmet, kot je kamen, je sila trenja zanemarljiva v primerjavi s težo kamna, njegova usmeritev pa je blizu parabole.

b) Pomembna je tudi oblika zagnanega predmeta. Če se zažene plošča ravnine v obliki Avionncito.

Po drugi strani pa je, če je isti list papirja kompakten v obliki kroglice, nastalo gibanje zelo podobno paraboli.

Primer 2

Iz vodoravnega dna se hitro izstreli izstrel iz kota 10 m/s in 60 °. To so isti podatki, s katerimi je bila razvita slika 1. S temi podatki najdem:

a) trenutek, v katerem doseže največjo višino.

Vam lahko služi: kakšne so toplotne lastnosti in kaj so? (S primeri)

b) največja višina.

c) hitrost pri največji višini.

d) Položaj in hitrost pri 1,6 s.

e) V trenutku, ko spet igra tla.

f) Vodoravni obseg.

Rešitev)

Navpična hitrost, odvisno od časa

v_in(t) = v_Oy - G t = v_tudi SENθ - G T = 10 Sen60º - 9.8 T = 8.66 - 9.8 t 

V času, ko je dosežena največja višina, je navpična hitrost za trenutek nič.   

8.66 - 9.8 t = 0 ⇒ t = 0.88 s.

Rešitev B)

Največja višina daje koordinata in Za trenutek, ko je dosežena ta višina:

in (0.88S) = Yo bom t -½ g t^2 = 0 + 8.66*0.88-½ 9.8 0.88^2 = 

3.83 m

Zato je največja višina 3.83 m.

Rešitev C)

Hitrost pri največji višini je vodoravna:

v_x(t) = v_vol = v_tudi cosθ = 10 cos60º = 5 m/s 

D) rešitev

Položaj pri 1.6 s je:

X (1.6) = 5*1,6 = 8,0 m

in (1.6) = 8.66*1.6-½ 9.8 1.62 = 1.31 m

Rešitev E)

Ko se koordinata dotakne in je preklicana, potem:

in (t) = 8.66*t -½ 9.8 t2 = 0 ⇒ t = 1,77 s

Rešitev F)

Vodoravni obseg je koordinata X v trenutku, ki igra tla:

X (1.77) = 5*1,77 = 8,85 m

Primer 3

Poiščite enačbo usmeritve s podatki 2.

Rešitev 

Parametrična enačba poti je:

x (t) = 5*t

in (t) = 8.66*t -½ 9.8 T^2

In kartezijansko enačbo dobimo s čiščenjem t prvega in zamenjavo v drugem

y = 8.66*(x/5) -½ 9.8 (x/5)^2

Poenostavitev:

y = 1,73 x - 0,20 x^2 

Reference

1. Str. Str. Teodorescu (2007). "Kinematika". Mehanski sistemi, klasični modeli: mehanika delcev. Springer.
2. Resnick, Halliday & Krane (2002). Fizika zvezek 1. Cecsa, Mehika.
3. Thomas Wallace Wright (1896). Elementi mehanike, vključno s kinematiko, kinetiko in statiko. E in fn Spon.
4. Wikipedija. Parabolično gibanje. Okreval od Es.Wikipedija.org.
5. Wikipedija. Gibanje izstrelkov.Pridobljeno iz.Wikipedija.org.