Horizontalne značilnosti streljanja, formule in enačbe, vaje

On Vodoravno streljanje Gre. Ne da bi upoštevali odpornost zraka, bo imela pot, ki jo je opisal mobilni telefon.

Projektiranje predmetov vodoravno je precej pogost. Projektili se vržejo z vsemi vrstami koncev: od kamnov, s katerimi so se na začetku zgodbe odklopili jezovi, do tistih, ki se izvajajo v športu z žogo in jim natančno sledijo množice.

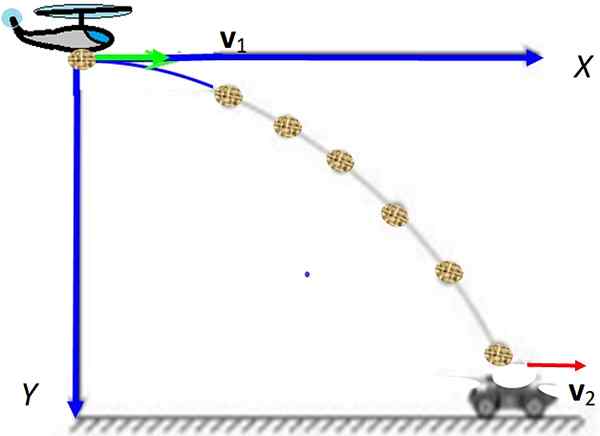
Slika 1. Vodoravno streljanje z rdečimi komponentami. Upoštevajte, da vodoravna komponenta ostane konstantna, medtem ko navpična raste. Vir: Wikimedia Commons.

[TOC]

Značilnosti

Glavne značilnosti horizontalnega streljanja so:

-Začetna hitrost, ki jo zagotavlja projektil, je pravokotna na gravitacijo.

-Gibanje poteka v ravnini, zato sta potrebni dve koordinati: x in in.

-To je narejeno iz določene višine h nad nivojem tal.

-Čas, ko izstrel v zraku, se imenuje čas letenja.

-Dejavniki, kot so zračna odpornost ali nihanja, se ne upoštevajo v vrednosti g.

-Oblika, velikost in masa izstrelkov ne vplivajo na njegovo gibanje.

-Gibanje se razkroji v dva hkratna gibanja: eno navpično navzdol pod delovanjem g; Drugi, vodoravni, s konstantno hitrostjo.

Formule in enačbe

Kinematografske enačbe za horizontalni zagon so pridobljene iz enačb za prosti padec in enačbe enotnega pravokotnega gibanja.

Vam lahko služi: notranja energija

Kot je na sliki 1 jasno prikazana animacija, je projektil opremljen z vodoravno začetno hitrostjo, označeno kot v_tudi = v_vol Yo (Krepko v tiskanem besedilu kaže, da je vektor).

Opozoriti je, da ima začetna hitrost velikost v_vol in je usmerjen vzdolž osi x, Kakšna je smer vektorja enote Yo. V animaciji je tudi opozorjeno, da začetna hitrost nima navpične komponente, a ker pade, se ta komponenta po zaslugi dejanja enakomerno povečuje g, gravitacijski pospešek.

Kar zadeva vodoravno komponento hitrosti, ostane konstanten, medtem ko gibanje traja.

Glede na to, kar je bilo rečeno, so položaji vzpostavljeni kot funkcija časa, tako na vodoravni osi kot na navpični osi. Desnica je vzeta kot osi +x, medtem ko je navzdol naslov -in. Vrednost gravitacije je G = -9.8 m/s² tudi -32 čevljev/s²:

x (t) = x_tudi + v_vol.t (vodoravni položaj); v_vol To je konstantno

in (t) = y_tudi + v_Oy.T - ½ g.t² (navpični položaj); v_in = v_Oy - g.T (navpična hitrost)

Položaj, hitrost, čas letenja in največji vodoravni razpon

Enačbe so poenostavljene, če izberejo naslednja začetna stališča: x_tudi = 0, in_tudi = 0 na mestu lansiranja. Poleg tega v_Oy = 0, Ker je mobilni telefon projiciran vodoravno. S to izbiro so enačbe gibanja takšne:

x (t) = v_vol.t; v_x = v_vol

in (t) = - ½ g.t²; v_in = - g.t

Ko čas ni na voljo, je enačba, ki povezuje hitrosti in premike. To velja za navpično hitrost, saj vodoravni ostaja konstantni v celotnem gibanju:

Vam lahko služi: kalcijev fluorid (caf2): struktura, lastnosti, uporabe

v_in² = v_Oy² + 2.g .y = 2.g.in

Čas letenja

Za izračun Čas leta t_let, Recimo, da je mobilni telefon projiciran z višine H na tleh. Ko je izvor izvozne točke izbran izvor referenčnega sistema, je, ko doseže tla, v položaju -H. Nadomestitev tega v enačbi 2) dobimo:

-H = - ½ g.t²_let

t_let = (2h/g)^½

Največji razpon

On Vodoravni doseg Ta čas dobimo z zamenjavo x (t):

x_Max = v_vol. (2H/g)^½

Rešene vaje

-Vaja rešena 1

Helikopter leti vodoravno in ohranja stalno dvig 580 m, ko sprosti škatlo, ki vsebuje hrano na begunskem taborišču. Škatla pristane na vodoravni razdalji 150 m od točke izstrelitve. Najti: a) čas letenja škatle.

b) hitrost helikopterja.

c) Kako hitro se je škatla dotaknila?

Rešitev

a) Višina h, iz katere se sprošča hrana, je H = 500 m. S temi podatki pri zamenjavi dobite:

t_let = (2h/g)^½= (2 x 580/9.8) ^½S = 10.9 s

b) helikopter nosi vodoravno začetno hitrost v_vol paketa in ker je eden od podatkov x_Max:

x_Max = v_vol. (2H/g)^½ ® v_vol = x_Max /(2H/g)^½= x_Max / t_let = 150 m/ 10.9 S = 13.8 m/s

c) Hitrost izstrelitve v vsakem trenutku je:

v_in = -g.T = -9.8 m/ s² x 10.9 S = -106.82 m/s = - 384.6 km/h

Negativni znak kaže, da se mobilni telefon premakne navzdol.

-Vaja Rešena 2

Iz ravnine, ki vodoravno leti na višini H = 500 m in 200 km/h Pade paket, ki mora padati na odprto vozilo, ki koraka 18 km/h na poti. V katerem položaju naj ravnino pusti paket v vozilu? Ne upoštevajte zračnega odpornosti ali hitrosti vetra.

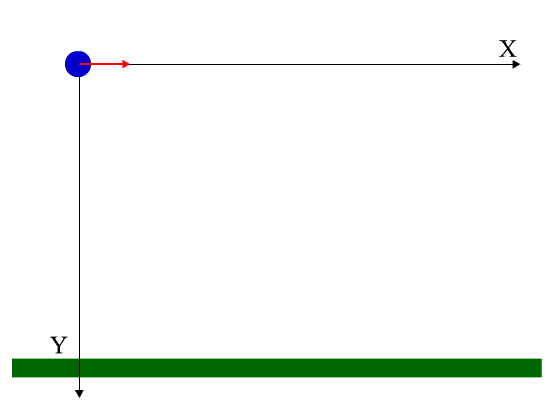
Vam lahko služi: dimenzijska analizaSlika 2. Shema za rešeno vajo 2. Vir: Pripravil F. Zapata.

Rešitev

Priročno je najprej vse enote prenesti v mednarodni sistem:

18 km/h = 6 m/s

200 km /h = 55 m /s

Obstajata dve mobilnici: ravnina (1) in vozilo (2) in izbrati je treba koordinatni sistem, da jih najdete oba. To je priročno na izhodišču paketa na ravnini. Paket je projiciran vodoravno s hitrostjo, ki jo nosi ravnina: v₁, Medtem ko se vozilo premakne na v₂ domnevno konstantno.

-Letalo

Začetni položaj: x = 0; y = 0

Začetna hitrost = v₁ (vodoravno)

Enačbe položaja: in (t) = -½g.t²  ; x (t) = v₁.t

-Vozilo

Začetni položaj: x = 0, y = -h

Začetna hitrost = v₂  (konstanta)

x (t) = x_tudi + v₂. t

Čas, ko traja paketni let, je:

t_let = (2h/g)^½ = (2 × 500/9.8)^½S = 10.1 s

V tem času je paket doživel horizontalni premik:

x_Max = v_vol . (2H/g)^½= 55 m/s x 10.1 s = 556 m.

V tem času se je vozilo premikalo tudi vodoravno:

x (t) = v₁.T = 6 m/s x10.1 s = 60.6 m

Če letalo takoj sprosti paket, ki ga vozilo vidi pod njim, ne bo mogel padati prav vanj. Da se to zgodi, ga mora vrgel nazaj:

D = 556 m - 60.6 m = 495.4 m.

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill. 74-84.
2. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 1. Kinematika. Uredil Douglas Figueroa (USB).117 - 164.
3. Gibanje izstrelkov. Okrevano od: Phys.Librettexts.org.
4. Rex, a. 2011. Osnove fizike. Pearson. 53-58.
5. Tippens, str. 2011. Fizika: pojmi in aplikacije. 7. izdaja. McGraw Hill. 126-131.