Vrste integralov
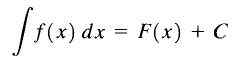
- 4464
- 64
- Mr. Shane Larkin
The Vrste integralov Da smo v izračunu, so nedoločeni integrali in definirani integrali. Čeprav imajo definirani integrali veliko več aplikacij kot nedoločeni integrali, se je najprej treba naučiti rešiti nedoločene integrale.
Ena najbolj privlačnih aplikacij definiranih integralov je izračun obsega trdne revolucije. Obe vrsti integralov imata enake lastnosti linearnosti, tudi tehnike integracije pa niso odvisne od vrste integrala.
Toda kljub temu, da je zelo podoben, obstaja glavna razlika; V prvi vrsti integrala je rezultat funkcija (ki ni specifična), medtem ko je pri drugi vrsti rezultat številka.
Osnovne vrste integralov
Svet integralov je zelo širok, toda znotraj tega lahko ločimo dve osnovni vrsti integralov, ki imata v vsakdanjem življenju veliko uporabnost.
1- Nedočasni integrali
Če je f '(x) = f (x) za vse x v domeni F, pravimo, da je F (x) antiderivacija, primitivna ali integral F (x).
Po drugi strani pa opazimo, da (f (x)+c) '= f' (x) = f (x), kar pomeni, da integral funkcije ni edinstven, saj dajanje različnih vrednosti stalnici C bomo dobili različne antiderivative.
Zaradi tega se f (x)+c imenuje nedoločen integral f (x), c pa se imenuje konstanta integracije in ga zapišemo na naslednji način:
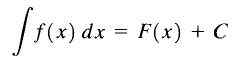 Nedoločen integral
Nedoločen integral Kot lahko vidimo, je nedoločen integral funkcije f (x) družina funkcij.
Na primer, če želite izračunati nedoločen integral funkcije f (x) = 3x², je treba najprej najprej najti antiderivat F (x).
Vam lahko služi: trinomialZlahka je opozoriti, da je f (x) = x³ antiderivativ, saj je f '(x) = 3x². Zato je mogoče sklepati, da
∫f (x) dx = ∫3x²dx = x³+c.
2- definirani integrali
Naj y = f (x) Resnična funkcija se nadaljuje v zaprtem intervalu [a, b] in bo f (x) antiderivacija f (x). Imenuje se definirani integral F (x) med omejitvami A in B do številke F (b) -f (a) in označuje na naslednji način:
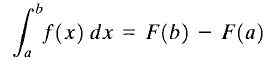 Teorem o temeljnem izračunu
Teorem o temeljnem izračunu Zgoraj prikazana formula je bolj znana kot "temeljni teorem izračuna". Tu se "A" imenuje spodnja meja in "B" se imenuje zgornja meja. Kot je razvidno, je dokončna integral funkcije številka.
V tem primeru se v intervalu izračuna, če se opredeljen integral f (x) = 3x² [0,3].
Za določitev te številke izberemo f (x) = x³ kot antiderivativ f (x) = 3x². Nato izračunamo f (3) -f (0), ki nas vrže kot rezultat 27-0 = 27. Za zaključek je definirani integral F (x) v intervalu [0,3] 27.
Upoštevati je mogoče, da če je G (x) = x³+3, potem je izbran g (x), je antiderivacija F (x), ki se razlikuje od f (x), vendar to ne vpliva na rezultat kot g (3) -g (0) = (27+3)-(3) = 27. Zaradi tega se v definiranih integralih ne pojavlja konstanta integracije.
Ena najbolj uporabnih aplikacij, ki jih ima ta vrsta integrala, je, da omogoča izračun območja (volumna) ravne številke (trdne revolucije), pri čemer vzpostavi ustrezne integracijske funkcije in omejitve (in os vrtenja).
Med definiranimi integrali lahko najdemo različne razširitve tega, kot so integralne črte, površinski integrali, nepravilni integrali, več integralov, med drugim z zelo koristnimi aplikacijami v znanosti in inženiringu.
Lahko vam služi: razlika med krogom in obodom (s primeri)Reference
- Kishan, h. (2005). Integralni računanje. Atlantski založniki in distributerji.
- Purcell, e. J., Varberg, d., & Rigdon, s. In. (2007). Izračun (Deveta ed.). Dvorana Prentice.

