Newtonove prošnje, eksperimente in vaje tretje zakona

The Newtonov tretji zakon, tudi poklican Zakon o ukrepanju in reakciji Potrjuje, da ko predmet izvaja moč nad drugim, slednji izvaja tudi na prvi sili enake razsežnosti in smeri ter nasprotnega smisla.

Isaac Newton je leta 1686 izdal svoje tri zakone v svoji knjigi Philosophiae Naturalis Principa Mathematica ali matematična načela naravne filozofije.

Vesoljska raketa prejme potreben pogon zaradi izgnanih plinov. Vir: Pixabay.

[TOC]

Pojasnilo in formule

Matematična formulacija Newtonovega tretjega zakona je zelo preprosta:

F₁₂ = -F_enaindvajset

Kliče se ena od sil dejanje In drugi je reakcija. Vendar je treba poudariti pomen te podrobnosti: oba delujeta na različnih predmetih. To počnejo tudi hkrati, čeprav ta terminologija napačno nakazuje, da se dejanje zgodi prej in reakcija po.

Ker so sile vektorji, so označene s krepko. Ta enačba kaže, da obstajata dva predmeta: objekt 1 in objekt 2. Moč F₁₂ To je tisti, ki izvaja predmet 1 na objektu 2. Moč F_enaindvajset je objekt 2 na objektu 1. In znak (-) poudarja, da nasprotujejo.

Ko natančno opazujemo Newtonov tretji zakon, obstaja pomembna razlika s prvima dvema: medtem ko se sklicujeta na en predmet, se tretji zakon nanaša na dva različna predmeta.

In če natančno razmišljate, interakcije zahtevajo pare predmetov.

Zato sile delovanja in reakcije niso preklicane ali uravnotežene, čeprav imajo enako velikost in smer, drugače pa: nanesejo se v različnih telesih.

Prijave

Interakcija z žogo - Zemlja

Tu je zelo vsakodnevna uporaba interakcije, povezane s Newtonovim tretjim zakonom: žoga, ki pade navpično, in Zemljo. Žoga pade na tla, ker zemlja izvaja privlačnost, ki je znana kot gravitacija. Ta sila povzroči, da žoga pade s stalnim pospeševanjem 9.8 m/s².

Vendar skoraj nihče ne razmišlja o dejstvu, da žoga na zemlji izvaja tudi privlačnost. Seveda zemlja ostaja nesprejemljiva, ker je njegova masa veliko večja od mase žoge in zato doživlja zaničevalno pospeševanje.

Druga pomembna vprašanje o Newtonovem tretjem zakonu je, da stik med obema predmetom, ki interakcija, ni potreben. Očitno je s pravkar navajanjem primera: žoga še vedno ne vzpostavi stika z zemljo, vendar vseeno vadi svojo privlačnost. In tudi žoga na zemlji.

Sila kot gravitacija, ki deluje zamenljivo, če obstaja stik med predmeti, kot da ni imena "Action Action Force". Namesto sil, kot sta trenje in normalno, zahtevajo, da so predmeti, ki so v interakciji, v stiku, zato se imenujejo "kontaktne sile".

Formule, pridobljene iz primera

Če se vrnete k nekaj krogličnih predmetov - Zemlja, izbirate hitrost P za žogo in T za zemljo in uporabi Newtonov drugi zakon za vsakega udeleženca tega sistema:

Lahko vam služi: diskretna spremenljivka: značilnosti in primeri

F_rezultat = m.do

Tretji zakon navaja, da:

m_Strdo_Str = - m_Tdo_T

do_Str = 9.8 m/s² usmerjeno navpično navzdol. Ker se to gibanje odvija vzdolž navpične smeri, se lahko izpusti z vektorskim zapisom (drzno); In izbirate smer navzgor kot pozitivno in navzdol kot negativno, imate:

do_Str = 9,8 m/s²

m_T ≈ 6 x 10 ^{24. 24} Kg

Ne glede na maso kroglice je pospešek zemlje nič. Zato opažamo, da žoga pade proti zemlji in ne obratno.

Delovanje rakete

Rakete so dober primer uporabe Newtonovega tretjega zakona. Raketa, prikazana na sliki na začetku, se dvigne zahvaljujoč pogonu vročega plina z veliko hitrostjo.

Mnogi verjamejo, da se to zgodi, ker ti plini nekako "podpirajo" vzdušje ali na tleh, da podpirajo in potisnejo raketo. Ne deluje tako.

Ker raketa izvaja trdnost na plinih in jih izriva nazaj, plini na raketi izvajajo silo, ki ima isti modul, vendar nasprotno smer. Ta sila je tista, ki zagotavlja raketo s pospeševanjem.

Če rakete nimate ročno, obstajajo tudi drugi načini, kako preveriti, ali Newtonov tretji zakon deluje za zagotavljanje pogona. Vodne rakete je mogoče zgraditi, v katerih je potreben potisk ponujena z voda na tlačni plin.

Treba je opozoriti, da začetek vodne rakete traja čas in zahteva veliko previdnostnih ukrepov.

Uporaba drsalk

Ceno cenovno ugodnejši in takojšen način za preverjanje učinka Newtonovega tretjega zakona je postavitev nekaj drsalk in promocijo stene.

Večino časa je povezana sposobnost, da se ukvarjajo s predmeti, ki so v gibanju. Drsalec se poganja nazaj zaradi sile, ki jo negibno izvaja na njem.

Kontaktne površine med seboj izvajajo kontaktne sile (normalne). Ko je knjiga podprta na vodoravni mizi, na njej izvaja normalno navpično silo. Knjiga na mizi izvaja navpično silo iste številčne vrednosti in nasprotnega smisla.

Otroški eksperiment: drsalci

Otroci in odrasli lahko doživijo Newtonov tretji zakon in preverijo, da sile ukrepov in reakcij ne razveljavijo in so sposobne zagotoviti gibanja.

Vsaka lahko poganjata dva drsalca na ledu ali na zelo gladki površini.

Razmislite o dveh drsalcih s precej različnim testom. So sredi drsališča z zaničevalnim trenjem in so sprva v mirovanju. V danem trenutku si med seboj potiskajo stalno moč z dlanmi rok. Kako se bosta premikala?

Vam lahko služi: uravnoteženje vektorja: izračun, primeri, vajeDva drsalca sta poganjana sredi drsališča. Vir: Benjamin Crowell (uporabnik Wikipedia Bcrowell) [CC BY-SA 3.0 (http: // creativeCommons.Org/licence/by-sa/3.0/]]

Pomembno je poudariti, da so, ker gre za površino brez trenja, edine neuravnotežene sile sile, ki jih drsalci medsebojno uporabljajo. Medtem ko sta teža in normalno delovanje na obeh, so te sile uravnotežene, od tistega, kar bi drsalci pospešili v navpični smeri.

Formule, uporabljene v tem primeru

Newtonov tretji zakon navaja, da:

F₁₂ = -F_enaindvajset

To pomeni, da je sila, ki jo ima drsalec 1 na 2, enaka po velikosti, do katere se 2 izvajata na 1, z isto smerjo in nasprotno smerjo. Upoštevajte, da se te sile uporabljajo za različne predmete, na enak način, kot so bile sile na žogi in zemlji v prejšnjem konceptualnem primeru.

m₁ do₁ = -M₂ do₂

Ker so sile nasprotne, bodo tudi pospeški, ki jih povzročajo, vendar bodo njihove velikosti drugačne, saj ima vsak drsalnik drugačno maso. Poglejmo pospešek, ki ga je pridobil prvi drsalec:

Če je masa prvega drsalca večja od mase drugega, bo njegov pospešek nižji. To je pričakovati, ker ima večjo inercijo. Najlažji drsalec pridobi večji pospešek. Če so mase enake, bodo tudi pospeški.

Torej je gibanje, ki se zgodi spodaj, ločitev obeh drsalcev v nasprotnih čutilih. Načeloma so bili drsalci v mirovanju sredi proge. Vsak na drugem izvaja silo, ki zagotavlja pospeševanje, medtem ko so roke v stiku, in potisk traja.

Po tem se drsalci oddaljujejo drug od drugega z enakomernim pravokotnim gibanjem, tako da ne delujejo neuravnotežene sile. Hitrost vsakega drsalca bo drugačna, če bodo tudi njihove mase.

Vaja rešena

Za reševanje težav, pri katerih je treba uporabiti Newtonove zakone, je treba skrbno risati sile, ki delujejo na objektu. Ta risba se imenuje "prosti diagram telesa" ali "izolirani diagram telesa". V tem diagramu sile, ki jih telo izvaja na drugih predmetih.

Če je v težavo vključen več kot en predmet, je to potrebno.

1- drsalci prejšnjega oddelka imajo ustrezne mase m₁ = 50 kg in m₂ = 80 kg. Med seboj se potiskajo s konstantno silo 200 n. Potis ima trajanje 0.40 sekund. Najti:

a) Pospešek, ki ga je vsak drsalec pridobil zaradi potiska.

b) hitrost vsakega, ko se loči

Rešitev

a) Vzemite kot vodoravno pozitiven naslov tistega, ki gre od leve proti desni. Uporaba Newtonovega drugega zakona z vrednotami, ki jih zagotavlja izjava, je:

F_enaindvajset = m₁do₁

Od kje:

Za drugega drsalca:

b) Za izračun hitrosti, ki jo nosijo ravno, ko je ločena, se uporabljajo kinematične enačbe enakomerno pospešenega rekvilinearnega gibanja:

Vam lahko služi: medsebojna induktivnost: formula/koeficient, aplikacije, vaje

Začetna hitrost je 0, saj so bili v mirovanju na sredini proge:

v_F = At

v_F1 = a₁t = -4 m/s² . 0.40 s = -1.6 m/s

v_F2 = a₂T = +2.5 m/s² . 0.40 s = +1 m/s

Rezultati

Kot je bilo pričakovano, oseba, ki je lažja, pridobi večji pospešek in zato hitrejšo hitrost. Zdaj opazujte naslednje o izdelku testa zaradi hitrosti vsakega drsalca:

m₁ v₁ = 50 kg . (-1.6 m/s) = - 80 kg.gospa

m₂ v₂ = 80 kg . 1 m/s = +80 kg.gospa

Vsota obeh izdelkov je 0. Izdelek mase s hitrostjo se imenuje količina gibanja P. Je vektor z isto smerjo in občutkom hitrosti. Ko so drsalci v mirovanju in v stiku, je mogoče domnevati, da tvorijo isti predmet, katerega količina gibanja je bila:

Str_tudi = (m₁ +m₂) v_tudi = 0

Ko je potisk končan, količina gibanja drsalnega sistema ostane 0. Zato je konzervirana količina gibanja.

Primeri Newtonovega tretjega zakona v vsakdanjem življenju

Hodi

Hoja je eno najbolj dnevnih dejanj, ki jih je mogoče izvesti. Če ga skrbno opazimo, je treba hojo potisniti nogo ob tla, tako da vrne enako in nasprotno silo na vznož.

Ko smo nenehno uporabljali Newtonov tretji zakon. Vir: Pixabay.

Ravno tista sila, ki ljudem omogoča hojo. Med letom ptice izvajajo moč v zraku in zrak potisne krila, tako da se ptica vozi naprej.

Gibanje avtomobila

V avtomobilu kolesa nahajajo na pločniku. Zahvaljujoč reakciji na pločniku se izvaja na silah pnevmatik, ki vozijo avto naprej.

Šport

V športni praksi so akcijske in reakcijske sile številne in imajo zelo aktivno udeležbo.

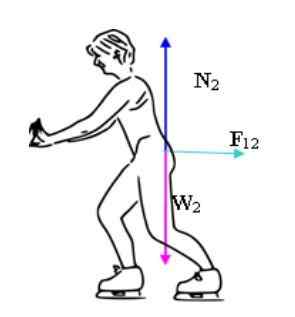
Na primer, poglejmo športnika z nogo, ki ga podpira zaganjalni blok. Blok zagotavlja normalno silo kot reakcijo na potisk, ki ga športnik izvaja na njem. Rezultat tega normalnega in teže hodnika ima za posledico horizontalno silo, ki športniku omogoča vožnjo naprej.

Športnik uporablja zaganjalni blok, da na izhod doda impulz naprej. Vir: Pixabay.

Požarne cevi

Drug primer, v katerem je Newtonov tretji zakon, je v gasilcih, ki držijo požarne cevi. Konec teh velikih cevi ima ročaj na šobi, ki jo mora gasilec držati, ko izide vodni curek, da se izognete neuspehu, ki se pojavi, ko voda izide s polno hitrostjo.

Iz istega razloga je priročno.

Reference

1. Giancoli, d.  2006. Fizika: načela z aplikacijami. Šesta izdaja. Dvorana Prentice. 80 - 82.
2. Rex, a. 2011. Osnove fizike. Pearson. 73 - 75.
3. Tipler, str. 2010. Fizično. Zvezek 1. 5. izdaja. Uredništvo se je vrtelo. 94 - 95.
4. Stern, d. 2002. Astronomi do Astronaves. Vzet od: pwg.GSFC.lonec.Gov.