Binomialni teorem

Kaj je binomni teorem?

On Binomialni teorem To je enačba, ki nam pove, kako se razvija izraz oblike (A+B)ⁿ Za nekaj naravnega števila n. Binomial ni nič drugega kot vsota dveh elementov, kot je (A+B). Prav tako nam omogoča, da poznamo izraz, ki ga je dal^kb^N-K Kakšen je koeficient, ki ga spremlja.

Ta teorem je običajno pripisan angleškemu izumitelju, fizičnemu in matematiku Sir Isaacu Newtonu; Vendar so bili najdeni različni zapisi, ki kažejo, da je bil njen obstoj že znan na Bližnjem vzhodu, okoli leta 1000.

Kombinirane številke

Binomni teorem matematično pove naslednje:

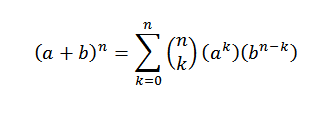
V tem izrazu sta A in B realna številka, n pa je naravno število.

Preden predstavimo demonstracijo, si oglejmo nekaj osnovnih konceptov, ki so potrebni.

Kombinatorična številka ali kombinacije N v K se izražajo na naslednji način:

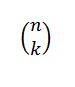
To izraža vrednost, koliko podskupine s K elementi lahko izberete iz niza N elementov. Njegov algebraični izraz je podan:

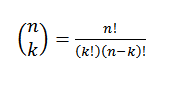
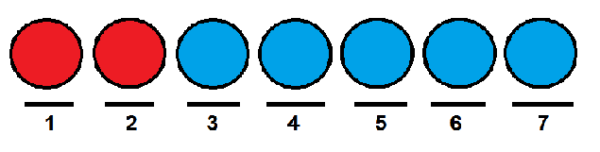
Poglejmo primer: predpostavimo, da imamo skupino sedmih kroglic, od katerih sta dve rdeči, ostali.

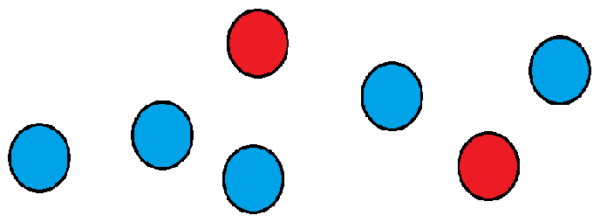
Želimo vedeti, na koliko načinov jih lahko naročimo po vrsti. Eden od načinov bi lahko postavil dva rdeča.

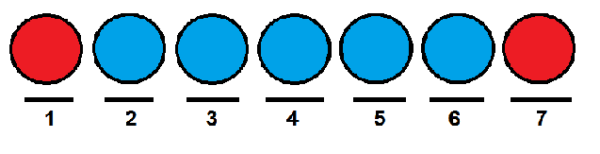
Podobno kot v prejšnjem primeru bi lahko Rdeče kroglice dali prvi in ​​zadnji položaj, druge pa zasedli z modrimi kroglicami.

Zdaj je učinkovit način za preštevanje, koliko načinov lahko naročimo kroglice v vrsti, ki uporablja kombinatorične številke. Vsak položaj lahko vidimo kot element naslednjega niza:

Vam lahko služi: popolne številke: kako jih prepoznati in primere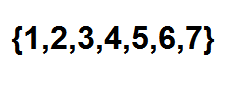

Spodaj je samo izbrati podskupino dveh elementov, v katerem vsak od teh elementov predstavlja položaj, ki ga bodo zasedle rdeče kroglice. To izbiro lahko naredimo v skladu z odnosom:

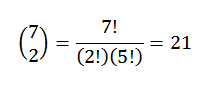
Na ta način imamo, da obstaja 21 načinov, kako naročiti takšne kroglice.

Splošna ideja tega primera bo zelo koristna pri demonstraciji binomnega teorema. Poglejmo določen primer: Če je n = 4, imamo (a+b)⁴, To ni nič drugega kot:

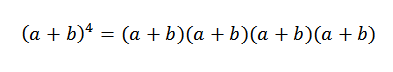
Ko razvijemo ta izdelek, imamo vsoto izrazov, pridobljenih z množenjem elementa vsakega od štirih dejavnikov (A+B). Tako bomo imeli izraze, ki bodo v obliki:

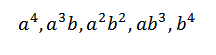
Če bi želeli pridobiti izraz obrazca⁴, Dovolj je le, da se pomnoži na naslednji način:

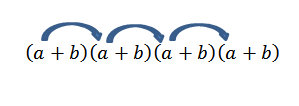
Upoštevajte, da obstaja samo en način za pridobitev tega elementa; Toda kaj se zgodi, če zdaj iščemo konec obrazca²b²? Ker sta "A" in "B" resnična številka, zato je vredno komutativnega zakona, moramo pridobiti ta izraz, da se pomnožimo s člani, kot kažejo puščice.

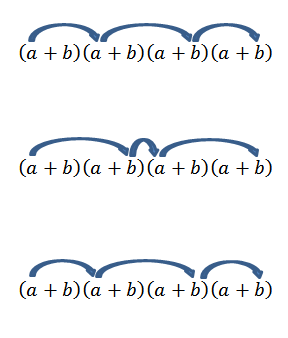
Izvajanje vseh teh operacij je ponavadi nekoliko dolgočasno, če pa vidimo izraz "a" kot kombinacijo, kjer želimo vedeti, koliko načinov lahko izberemo dva "A" iz nabora štirih dejavnikov, lahko uporabimo idejo Prejšnji primer prejšnjega primera. Torej, imamo naslednje:

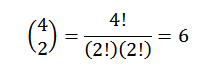
Tako vemo, da v končnem razvoju izraza (A+B)⁴ Imeli bomo natanko 6²b². Z isto idejo za druge elemente morate:

Vam lahko služi: transcendentne številke: kaj so, formule, primeri, vaje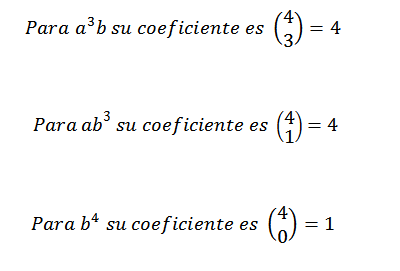

Nato dodamo zgoraj pridobljene izraze in moramo:

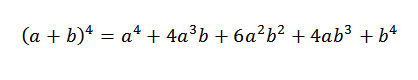
To je formalna demonstracija za splošni primer, v katerem je "n" katero koli naravno število.

Demonstracija

Upoštevajte, da so izrazi pri razvoju (A+B)ⁿ So iz oblike do^kb^N-K, kjer je k = 0,1,…, n. Z idejo prejšnjega primera imamo način, da izberemo "k" spremenljivke "A" A "N" dejavnikov:

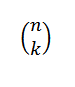
Pri izbiri na ta način samodejno izberemo spremenljivke N-K "B". To sledi, da:

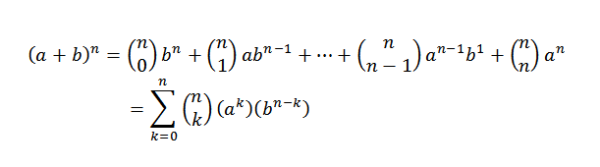
Primeri

Glede na (A+B)⁵, Kakšen bi bil vaš razvoj?

Za binomialni teorem moramo:

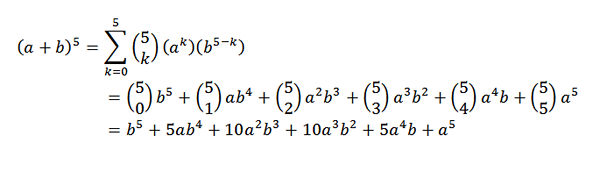
Binomski teorem je zelo koristen, če imamo izraz, v katerem želimo vedeti, kakšen je koeficient določenega izraza, ne da bi morali opraviti celoten razvoj. Kot primer lahko vzamemo naslednje neznano: kakšen je koeficient x⁷in⁹ V razvoju (x + y)¹⁶?

Za binomni izrek imamo, da je koeficient:

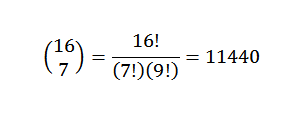
Drug primer bi bil: Kakšen je koeficient x⁵in⁸ V razvoju (3x-7y)¹³?

Najprej izraz prepišemo na priročen način; to je:

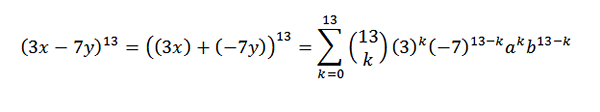
Nato s pomočjo binomialnega teorema imamo, da je iskani koeficient, ko imate k = 5

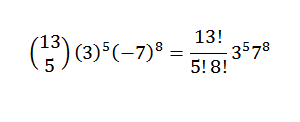
Drug primer uporabe tega izrek je v predstavitvi nekaterih skupnih identitet, kot so tiste, ki jih bomo omenili spodaj.

Identiteta 1

Če je "n" naravno število, moramo:

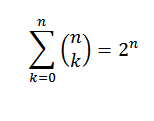
Za demonstracijo uporabljamo binomni teorem, kjer tako "a" kot "b" vzameta vrednost 1. Potem imamo:

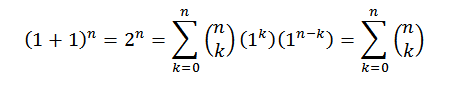
Na ta način smo dokazali prvo identiteto.

Vam lahko služi: naključne izbire z ali brez zamenjave

Identiteta 2

Če je "n" naravno število, potem

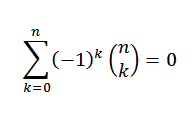
Za binomialni teorem moramo:

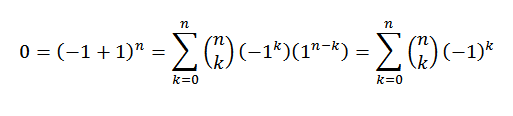
Še ena demonstracija

Lahko naredimo drugačno demonstracijo za binomni izrek z uporabo induktivne metode in identitete Pascala, kar nam pove, da sta, če sta "n" in "k" pozitivna cela števila, ki izpolnjujejo n ≥ k, potem:

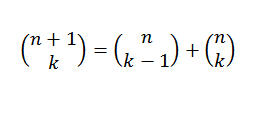
Indukcijska demonstracija

Poglejmo, da je induktivna osnova izpolnjena.  Če je n = 1, moramo:

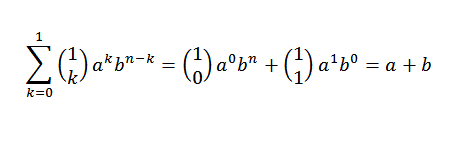
Dejansko vidimo, da je izpolnjen. Zdaj bodisi n = j tak, da je izpolnjen:

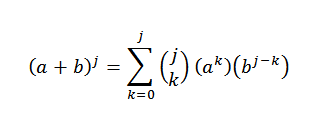
Želimo videti, da je za n = j+1 res, da:

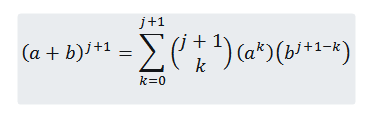
Torej moramo:

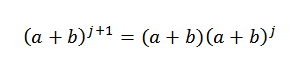
Po hipotezi vemo, da:

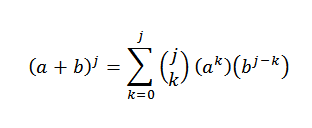
Nato z uporabo distribucijske lastnosti:

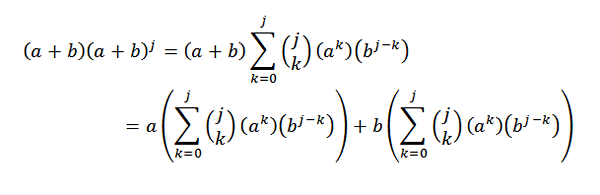
Kasneje je razvoj vsakega od povzetkov:

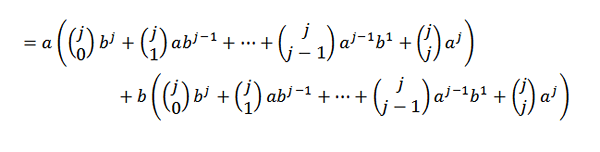
Zdaj, če se priročno združimo, moramo:

S Pascalovo identiteto moramo:

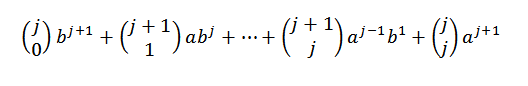
Končno upoštevajte, da:

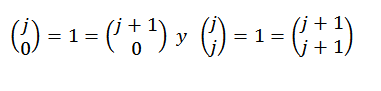
Zato vidimo, da je binomski teorem izpolnjen za vsak "n", ki pripada naravnemu številu, in s tem se test konča.

Radovednosti

Kombinatorična številka (NK) se imenuje tudi binomni koeficient, ker je ravno koeficient, ki se pojavlja v razvoju binoma (A+B)ⁿ.

Isaac Newton je posplošil ta teorem za primer, v katerem je eksponent resnično število; Ta teorem je znan kot Newtonov binomni teorem.

Ta rezultat je bil že v antiki, znan po posebnem primeru, v katerem je n = 2. Ta primer je omenjen v Predmete Euclida.