Miletus tak izrek

Pojasnjujemo prvo in drugo teoremo takšnih, s primeri in reševanimi vajami

Slika 1.- Teorem zgodb

Kaj je takšno?

On takšen izrek Od Miletusa se dejansko nanaša na več teoremov o geometriji, ki jih pripisujejo modrim starodavnim Grčiji Thales iz Miletusa, ki je živel od 624 do 546 AC v Miletu, sedanja Turčija.

Poleg matematika in geometra je bil takšen filozof, prepoznan po svoji veliki ostrini. Govori se, da mu je uspelo izmeriti višino velike piramide z uporabo enega od svojih teoremov.

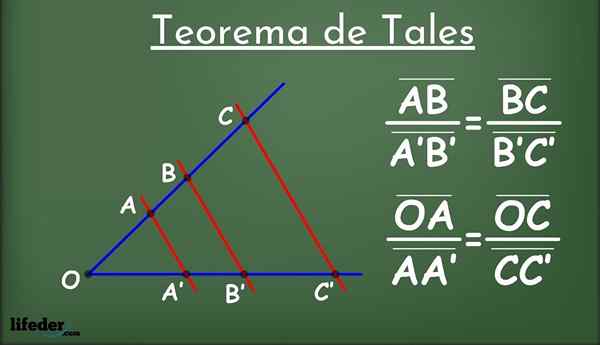
On Prvi teorem takega Nanaša se na segmente, ki jih skupina vzporednih črk določa v dveh vrsticah v ravnini. Ti segmenti ohranjajo razmerje sorazmernosti, kot bomo videli kmalu, ki se razširi na stranice dveh trikotnikov, pod pogojem, da so izpolnjeni določeni pogoji.

Ta teorem je v praksi izredno uporaben, saj omogoča določitev višine zelo visokih ali težkih za dostop do struktur, ne da bi jih bilo treba neposredno izmeriti. Prav to je storilo zgodbe, ko je izmeril višino velike piramide.

Svoje strani Drugi teorem tega Povezave točke, ki pripadajo obodu s pravokotnim trikotnikom, registriranim v njem, katere hipotenuza sovpada z njegovim premerom.

Prvi teorem takega

Biti dve črti v ravnini, imenovani l₁ in l₂ (v modri barvi na sliki 1) in skupino črt, vzporednih med seboj (v rdeči barvi), ki sekajo L₁ in l₂.

Vzporedne črte razdelijo črte na segmente l₁ in l₂: Ab, a'b ', bc, b'c' in tako naprej. Med soočenimi segmenti se vzpostavi naslednji sorazmernost:

Na primer, na tej sliki se ukrep segmenta "X" izračuna s teoremom takega, saj črte presekajo več vzporednic, ki določajo segmente z znano dolžino:

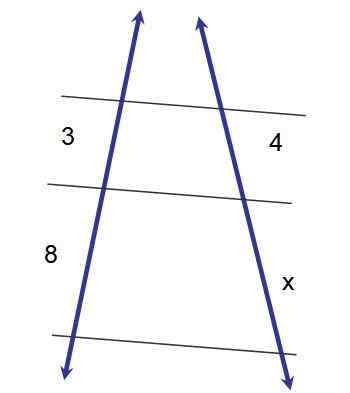Lahko vam služi: medsebojno izključujoči dogodki: lastnosti in primeriSlika 2.- Uporaba prvega takšnega teorema za določitev mera segmenta x. Vir: f. Zapata.

3x = 32

x = 32/3 ≈ 10.7

Takšen izrek za podobne trikotnike

Teorem se lahko razširi na trikotnike na naslednji način: predpostavimo, da obstaja ABC trikotnik, na katerem je vzporedni segment narisan na eno od njegovih strani. Na ta način dobimo dva podobna trikotnika: ABC in DEC, katerih notranji koti so skladni, to je, da imata enakega ukrepa.

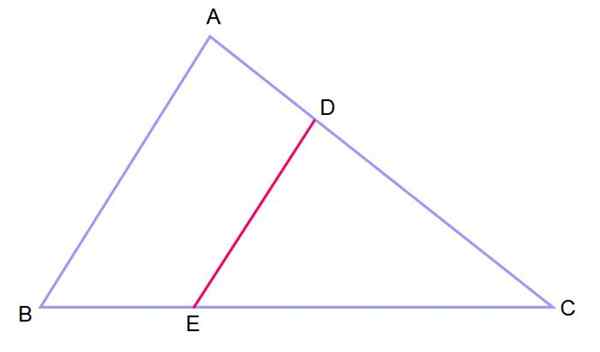Slika 3.- Dva trikotnika v položaju takšnih z dvema vzporednima stranicama in skupnim kotom sta podobna. Vir: f. Zapata.

Ko imate na ta način razporejeni dva trikotnika, se reče, da sta na takem položaju.

Razmerje sorazmernosti med segmenti se zviša na enak način kot pri vzporednih linijah:

Ki je enakovreden temu drugemu, med ustreznimi stranicami vsakega trikotnika, imenovane tudi homologne strani:

Vsak od teh količnikov se imenuje Razlog podobnosti. V podobnih trikotnikih je razlog za podobnost enak količniku med obodom in kvadratom razmerja podobnosti je enak količniku med območji.

Nato je primer, v katerem je mogoče tak teorem uporabiti za podobne trikotnike in ugotoviti, koliko je vredna neznana stran x.

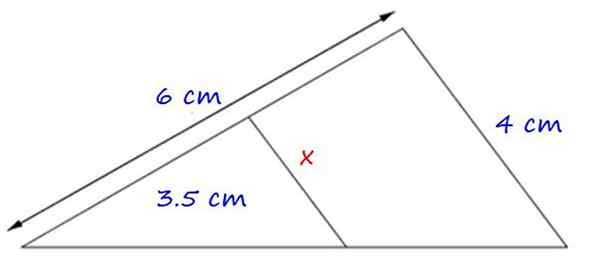Slika 4.- Primer aplikacije prvega takšnega izreka. Vir: f. Zapata.

Trikotniki so podobni, saj imajo skupni kot in stranica x in 4 cm sta vzporedna.

Zato je sorazmernost med ustreznimi stranmi:

In vrednost X je enostavno očistiti:

x = (4 × 3.5) ÷ 6 cm = 2.3 cm

Drugi teorem tega

Ta teorem se nanaša na trikotnik, katerega točki so točke, ki pripadajo obodu, kar pomeni, da je v njem registriran.

V tem primeru teorem ugotovi, da kadarkoli hipotenusa ustreza premeru oboda, je tako sleden trikotnik pravokotnik, torej eden od njegovih notranjih kotov 90 °, kot je prikazano na sliki 5 na levo.

Vam lahko služi: simbolizacija izrazov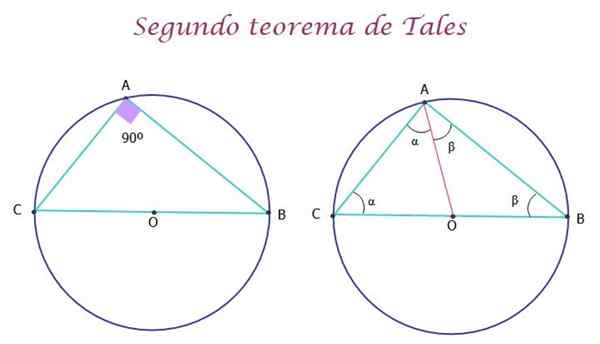Slika 5.- Drugi izrek takšnih navaja, da je trikotnik, registriran v obodu, pravokotnik. Vir: f. Zapata.

Demonstracija drugega teorema takšnih

Demonstracija teorema je zelo preprosta. Na zgornji sliki desno je bil segment AO narisan v rdeči barvi, da tvorita dva trikotnika AOC in AOB, ki sta izoscele, saj so stranice OA, OC in OB radijske radijske sprejemnike in zato merijo enako.

Na ta način imajo trikotniki dva enaka kota, ki sta α in β. Zdaj je za originalni trikotnik ABC, kot za vsak trikotnik, izpolnjeno, da je vsota ukrepov njegovih notranjih kotov enaka 180 °:

α + (α + β) + β = 180 °

Torej:

2α + 2β = 180 °

Zato:

2 (α +β) = 180 °

α +β = 90 °

Kar dokazuje, da ima ABC trikotnik notranji kot 90 ° in je zato pravi trikotnik.

Primer

Na naslednji sliki je trikotnik ABC izosceles in pravokotnik (izoretangle trikotnik), ki je obod oboda, ki je enak 25 cm. Koliko sta segmenti AC in AB?

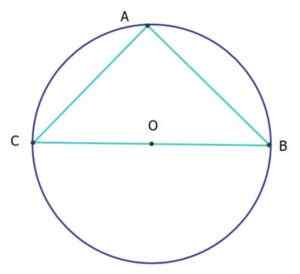
Obod oboda je njegova dolžina l, ki je odvisna od premera d po formuli:

L = πd

Zato meri premer, ki je segment CB, meri:

D = cb = l/ π = 25 cm/ π = 7.96 cm.

Ker je trikotnik izosceles, to pomeni, da njeni akutni koti merijo 45 °. Ker je hipotenuza trikotnika premer oboda, lahko na primer uporabimo trigonometrično razmerje 45:

Sen 45 ° = AC/CB

Ac = cb × sin 45 ° = 7.96 cm × greh 45 ° = 5.64 cm

Vam lahko služi: teorem moire

AB stran ima enak ukrep: 5.64 cm, saj je trikotnik izosceles.

Takšne teoremske aplikacije

Prvi tak teorem je mogoče uporabiti za poznavanje razdalj, ki jih ni enostavno meriti. Govori se, da je takšen odpotoval v Egipt in tam na zelo iznajdljiv način določil višino velike piramide.

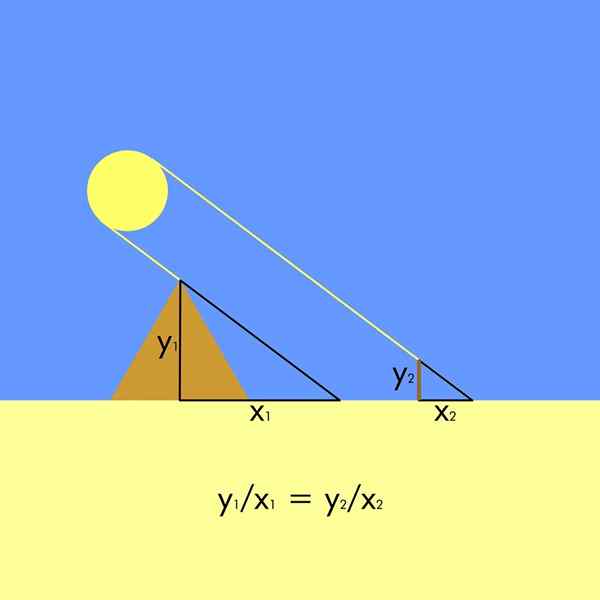
Za to je bilo potrebno. Tako nastaneta dva podobna trikotnika, saj imajo sončni žarki vzporedno vpajanje.

Na sliki je višina piramide in₁ In njegova senca je x₁, Medtem ko je višina vložka in₂ (Nekateri kronisti trdijo, da so takšni porabili svojo višino) in njihova senca je x₂. Ker so trikotniki podobni, se oblikuje naslednje sorazmerno razmerje:

Je zelo enostavno očistiti višino piramide in₁:

in₁ = x₁∙ (in₂ ÷ x₂)

Reference

1. Aleksander, d. 2013. Geometrija. 5. Izdaja. Cengage učenje.
2. Requena, b. Takšen izrek. Okrevano od: univerzeformulas.com.
3. Matematična dvorana. Tales de Mileto in velika piramida. Pridobljeno iz: salonmatematic.com
4. Superprof didaktični material. Miletus takšen. Okrevano od: Superprof.je.
5. Thales in teorem podobnosti. Dve zelo stari težavi. Okreval od: edu.Xunta.Gal.