Steinerjeva razlaga teorema, aplikacije, vaje

On Steinerjev teorem, znati tudi kot Teorem vzporedne osi, Omogoča oceno inercijskega momenta razširjenega telesa, okoli osi, ki je vzporedna z drugo, ki poteka skozi sredino mase predmeta.

Odkril ga je švicarski matematik_Cm vztrajnost predmeta glede na osi, ki poteka skozi njen CM in I Mass Center_z Inercijski trenutek glede na drugo vzporedno osi do tega.

Slika 1. Pravokotna vrata, ki se vklopijo na svoje radosti. Vir: Pixabay.

Znana razdalja D, ki ločuje osi in maso M od zadevnega telesa, je vztrajnost glede na osi Incognito:

Yo_z = I_Cm + Md²

Inercijski trenutek kaže, kako enostavno je, da se predmet vrti okoli določene osi. Odvisno ni samo od telesa telesa, ampak od tega, kako je porazdeljeno. Zaradi tega je znano tudi kot Rotacijska inercija, Biti vaše enote v mednarodnem sistemu KG . m².

Teorem kaže, da je vztrajnostni trenutek Yo_z Vedno je večji od inercijskega trenutka Yo_Cm v znesku, ki ga daje M.D².

[TOC]

Prijave

Ker se predmet lahko vrti okoli številnih osi, v tabelah to.

Vam lahko služi: pravokotno gibanje: značilnosti, vrste in primeri

Na primer, vrata se običajno ne vrtijo okoli osi, ki poteka skozi njeno masno središče, ampak glede na stransko osi, kjer se tečaji držijo.

Ko poznate inercijski trenutek, je mogoče izračunati kinetično energijo, povezano z vrtenjem na tej osi. Ja K je kinetična energija, Yo inercijski moment okoli zadevne osi in Ω Kotna hitrost je izpolnjena:

K = ½ i.Ω²

Ta enačba je zelo podobna zelo znani formuli kinetične energije za masni objekt M premikanje s hitrostjo v:  K = ½ m.v². In je to, da je vztrajnostni trenutek ali rotacijska inercija Yo igra v rotaciji isto vlogo kot testo M V prevodu.

Demonstracija Steinerjevega teorema

Inercijski trenutek razširjenega predmeta je opredeljen kot:

I = ∫r² Dm

Kje Dm Je neskončno majhna masa mase in r To je razdalja med Dm in osi vrtenja z. Na sliki 2 ta osi prečka središče mase CM, vendar je lahko kdorkoli.

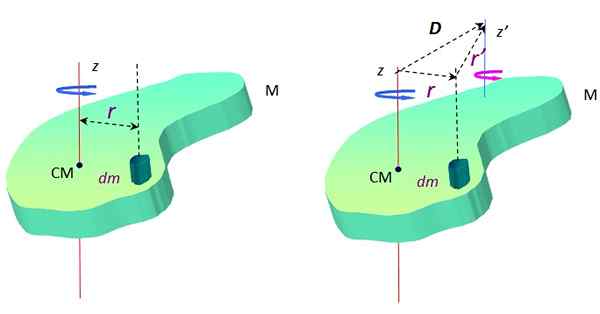Slika 2. Predmet, razširjen v vrtenju okoli dveh vzporednih osi. Vir: f. Zapata.

Okoli druge osi  z, Inercijski trenutek je:

Yo_z= ∫ (R ')² Dm

Zdaj po trikotniku, ki ga tvorijo vektorji D, r in R ' (Glej sliko 2 desno), obstaja vektorska vsota:

r + R ' = D   → R ' = D - r

Trije vektorji so na ravnini predmeta, ki je lahko Xy. Izvor koordinatnega sistema (0,0) je izbran v CM, da se olajša izračune, ki sledijo.

Na ta način kvadratni modul vektorja R ' je:

Lahko vam služi: Biofizika: Zgodovina, katere študije, aplikacije, koncepti, metode

(R ')² = (D_x- r_x)² +(D_in - r_in)² =

= D_x² + D_in² +r_x² + r_in2 -2d_xr_x - 2 d_inr_in =

= D² + r²  - 2d_xr_x - 2 d_inr_in

Zdaj je ta razvoj nadomeščen v integralu trenutka inercije i_z in uporabljena je tudi definicija gostote dm = ρ.DV:

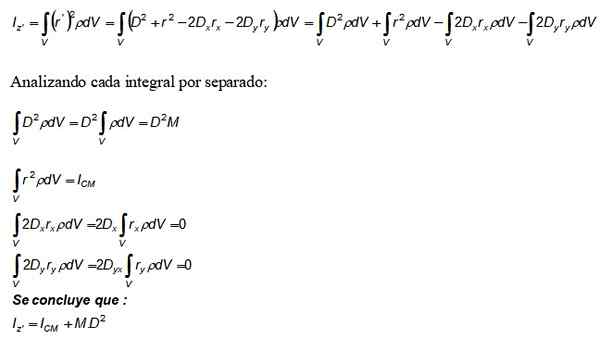
Izraz m. D² ki se pojavlja v Steinerjevem teoremu iz prvega integrala, drugi pa je vztrajnost glede na osi, ki poteka skozi CM.

Tretji in četrti integrali sta vredni 0, saj po definiciji predstavljata položaj CM, ki je bil izbran za izvor koordinatnega sistema (0,0).

Rešene vaje

-Vaja rešena 1

Pravokotna vrata slike 1 imajo maso 23 kg, 1,30 široka in visoka 2,10 m. Določite inercijski trenutek vrat glede osi, ki poteka skozi veselje, ob predpostavki, da so vrata tanka in enakomerna.

Slika 3. Shema za primer razrešen 1. Vir: Modified Pixabay.

Rešitev

Iz tabele inercijskih trenutkov, za pravokotno ploščo mase m in dimenzij do in b, Inercijski moment glede na osi, ki poteka skozi njegovo središče mase, je: i_Cm = (1/12)M(do² + b²).

Domneva se homogena vrata (pristop, saj vrata figure verjetno niso toliko). V tem primeru središče množice prehaja skozi njeno geometrijsko središče. Na sliki 3 je bila narisana os, ki poteka skozi masno središče in je tudi vzporedna z osi, ki poteka skozi veselje.

Yo_Cm = (1/12) x 23 kg x (1.30²+2.10²) m² = 11.7 kg.m²

Vam lahko služi: kaj je geoid?

Uporaba Steinerjevega teorema za osi zelene vrtenja:

I = i_Cm + Md² = 11.7 kg.m² + 23 kg x 0.652 m² = 21.4 kg.

-Vaja Rešena 2

Poiščite inercijski moment tanke homogene palice, ko se vrti glede na osi, ki poteka skozi enega od njegovih koncev, glej sliko. Ali je večji ali manj kot inercijski trenutek, ko se vrti okoli svojega središča? Ker?

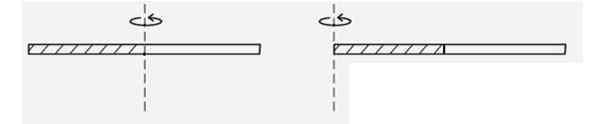Slika 4. Shema za primer rešena 2. Vir: f. Zapata.

Rešitev

Po inercijskih trenutkih, momen inercije Yo_Cm tanke palice testa M in dolžina L je: Yo_Cm = (1/12) ml²

In Steinerjev teorem navaja, da ko se vrti okoli osi, ki gre skozi en konec d = l/2, ostaja:

I = i_Cm + Md² = (1/12) ml² + M (l/2)² = (1/3) ml²

Je star.

Vpliv razdalje do osi vrtenja ni linearn, ampak kvadraten. Masa, ki je dvakrat razdalja, ki bo imela drugi trenutek vztrajnosti, sorazmerna z (2d)² = 4D².

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill. 313-340.
2. Državna univerza Georgia. Rotacijsko gibanje. Okrevano od: Phys.Nthu.Edu.Tw.
3. Teorem vzporedne osi. Okrevano od: hiperfizika.PHY-ASST.GSU.Edu.
4. Rex, a. 2011. Osnove fizike. Pearson. 190-200.
5. Wikipedija. Teorem vzporedne osi. Pridobljeno iz: v.Wikipedija.org