Teorem Bolzano

Pojasnjujemo, kaj je Bolzanov izrek, njegove aplikacije in dali rešene vaje

Kaj je Bolzanovo teorem?

On Teorem Bolzano Ugotavlja, da če je funkcija neprekinjena na vseh točkah zaprtega intervala [a, b] in je izpolnjeno, da imata slika "a" in "b" (pod funkcijo) nasprotne znake Ena točka "C" v odprtem intervalu (a, b), tako da bo funkcija, ocenjena v "C", enaka 0.

Ta teorem je leta 1850 izjavil filozof, teolog in matematik Bernard Bolzano. Ta znanstvenik, rojen na sedanji Češki republiki, je bil eden prvih matematike v zgodovini, ki je formalno predstavil lastnosti neprekinjenih funkcij.

Pojasnilo teorema

Bolzanov teorem je znan tudi kot teorem vmesnih vrednosti, ki pomaga pri določanju posebnih vrednosti, zlasti ničle, nekaterih resničnih funkcij resnične spremenljivke.

V dani funkciji se f (x) nadaljuje -to je, da sta f (a) in f (b) povezana z krivuljo, kjer je f (a) pod osi x (je negativen) in f (b) Z osi X (je pozitiven) ali obratno, na osi X bo na osi X, ki bo predstavljala vmesno vrednost "C", ki bo med "A" in "B", in vrednostjo. od f (c) bo enako 0.

Pri grafični analizi Bolzanovega teorema je mogoče vedeti, da je za katero koli neprekinjeno funkcijo F, opredeljeno v intervalu [a, b], kjer je F (a)_*f (b) je manj kot 0, v intervalu bo vsaj ena korenina "C" te funkcije (a, b).

Ta teorem ne določa števila točk, ki obstajajo v tem odprtem intervalu, pravi le, da obstaja vsaj 1 točka.

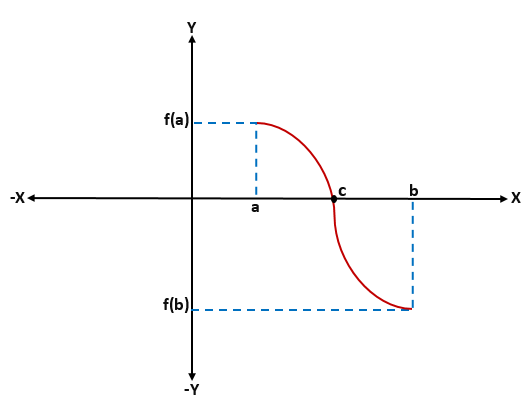
Demonstracija teorema Bolzano

Da bi pokazali Bolzanovo izrek, se domneva, da brez izgube splošnosti f (a) 0; Na ta način je lahko veliko vrednosti med "a" in "b", za katere f (x) = 0, vendar je treba le pokazati, da obstaja ena.

Vam lahko služi: namišljene številke: lastnosti, aplikacije, primeri

Začne ocenjevati F na sredini točke (A+B)/2. Če je F ((A+B)/2) = 0, se test konča tukaj; V nasprotnem primeru je F ((A+B)/2) pozitiven ali negativen.

Izbran je ena od polovic intervala [a, b], tako da so znaki funkcije, ocenjene na koncih, različni. Ta nov interval bo [A1, B1].

Zdaj, če je F ocenjen na sredini točke [A1, B1], ni nič, potem se prej izvede ista operacija; To pomeni, da je ena polovica tega intervala, ki ustreza stanju znakov. Bodite ta nov interval [A2, B2].

Če se ta postopek nadaljuje, bosta na voljo dve nasledniki an in bn, tako da:

an raste in bn se zmanjšuje:

a ≤ a1 ≤ a2 ≤ ... ≤ an ≤ .. . ≤ .. . ≤ bn ≤ .. . ≤ b2 ≤ b1 ≤ b.

Če se izračuna dolžina vsakega intervala [ai, bi], boste morali:

B1-A1 = (B-A)/2.

B2-A2 = (B-A)/2².

.. .

bn-an = (b-a)/2^n.

Zato je meja, ko se N nagiba k neskončnosti (Bn-A), enaka 0.

Uporaba tega an raste in omejena, bn pa se zmanjšuje in omejuje, obstaja vrednost "c", tako da:

a ≤ a1 ≤ a2 ≤ ... ≤ an ≤ .. .≤ C ≤ .. . ≤ bn ≤ .. . ≤ b2 ≤ b1 ≤ b.

Omejitev LIM je "C" in meja bn je tudi "C". Zato glede na katero koli δ> 0 vedno obstaja "n", tako da je interval [an, bn] v intervalu (C-Δ, C+δ).

Zdaj je treba pokazati, da je f (c) = 0.

Če je f (c)> 0, potem je F neprekinjen, obstaja ε> 0, tako da je F skozi interval pozitiven (C -ε, C+ε). Vendar pa, kot je navedeno zgoraj, obstaja vrednost "N", tako da je F -spreminjanje v [an, bn] in poleg tega [an, bn] vsebovano v (c -ε, c+ε), kaj kaj je protislovje.

Če je f (c) 0 tako, da je f negativen v celotnem intervalu (c -ε, c+ε); Vendar obstaja vrednost "N", ki se vpisa v [an, bn]. Izkazalo se je, da je [AN, BN] vsebovan znotraj (C -ε, C+ε), kar je tudi protislovje.

Vam lahko služi: znaki združevanja

Zato je f (c) = 0 in to je tisto, kar je bilo želelo dokazati.

Za kaj je teorem Bolzano?

Iz svoje grafične razlage se Bolzanov teorem uporablja za iskanje korenin ali ničle v neprekinjeni funkciji z bisenzijo (pristopo.

Če torej funkcija spreminja znak v intervalu, se funkcija F oceni na sredini, ki je izražena na naslednji način: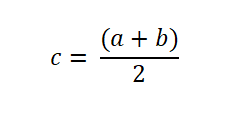Koren najdemo, ko je f (c) = 0. Če ne, se analizira znak F (c), da se ugotovi, ali je nasprotovan znaku F (a) ali znanosti F (b).

Potem se vzame interval [a, c] ali [c, b] tam, kjer pride do spremembe znaka, postopek pa se ponavlja, dokler interval ni manj in manj, da se približate želeni vrednosti; torej na vrednost, ki jo ima funkcija 0.

Če povzamemo, če želite uporabiti teorem Bolzano in tako najti korenine, omejiti ničle funkcije ali dati rešitev enačbe, se izvedejo naslednji koraki:

1. Preverjeno je, ali je F neprekinjena funkcija v intervalu [a, b].
2. Če interval ni podan, je treba najti enega, kjer je funkcija neprekinjena.
3. Preverjeno je, če konci intervala dajejo nasprotne znake, ko jih ocenimo v F.
4. Če nasprotnih znakov ne dobijo, je treba interval razdeliti na dva podtemna s pomočjo sredine točke.
5. Ocenite funkcijo na sredini in preverite, ali je izpolnjena hipoteza Bolzano, kjer je F (a) _* f (b) < 0.
6. Odvisno od znaka (pozitivnega ali negativnega) najdene vrednosti se postopek ponovi z novim podintralom, dokler omenjena hipoteza ni izpolnjena.

Vam lahko služi: nelinearno programiranje: metode in vaje

Rešene vaje

Vaja 1

Ugotovite, ali je funkcija f (x) = x² - 2 ima v intervalu vsaj eno resnično rešitev [1,2].

Rešitev

Imate funkcijo f (x) = x² - 2. Kot je polinom, to pomeni, da je v katerem koli intervalu neprekinjen.

Zahteva se, ali ima v intervalu resnično rešitev [1, 2], zato morate zdaj le zamenjati konce intervala v funkciji, da poznate ta znak in vedeti, ali izpolnjujejo stanje bivanja drugačen:

f (x) = x² - 2

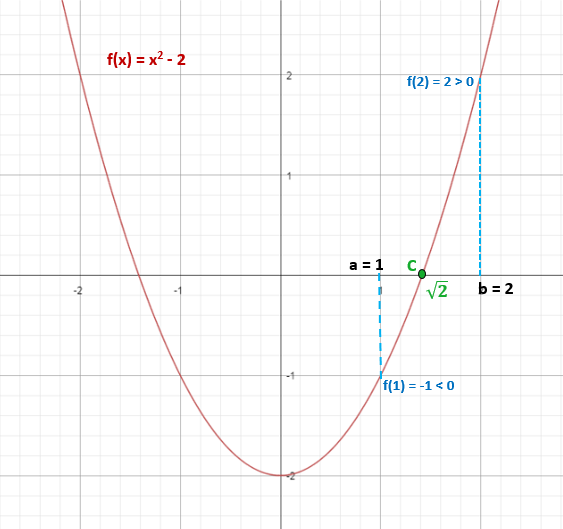
f (1) = 1² - 2 = -1 (negativno)

f (2) = 2² - 2 = 2 (pozitivno)

Zato znak f (1) ≠ znak f (2).

To zagotavlja, da obstaja vsaj ena točka "C", ki spada v interval [1,2], v kateri je f (c) = 0.

V tem primeru lahko vrednost "C" izračunamo enostavno na naslednji način:

x² - 2 = 0

x = ± √2.

Tako √2 ≈ 1,4 spada v interval [1,2] in izpolnjuje, da je F (√2) = 0.

Vaja 2

Dokažite, da enačba x⁵ + x + 1 = 0 ima vsaj eno resnično rešitev.

Rešitev

Najprej opazimo, da je f (x) = x⁵ + X + 1 je polinomna funkcija, kar pomeni, da je v vseh resničnih številkah neprekinjena.

V tem primeru ni naveden interval, zato morate za oceno funkcije in najti spremembe znaka intuitivno, po možnosti blizu 0

Če se uporablja interval [0, 1], mora:

f (x) = x⁵ + x + 1.

f (0) = 0⁵ + 0 + 1 = 1> 0.

f (1) = 1⁵ + 1 + 1 = 3> 0.

Ker ni sprememb znakov, se postopek ponovi z drugim intervalom.

Če se uporablja interval [-1, 0], morate:

f (x) = x⁵ + x + 1.

f (-1) = (-1)⁵ + (-1) + 1 = -1 < 0.

f (0) = 0⁵ + 0 + 1 = 1> 0.

V tem intervalu je sprememba znaka: Znak F (-1) ≠ Znak F (0), kar pomeni, da je funkcija f (x) = x⁵ + X + 1 ima v intervalu vsaj en pravi koreninski "C" [-1, 0], tako da je f (c) = 0. Z drugimi besedami, res je, da x⁵ + x + 1 = 0 ima resnično rešitev v intervalu [-1,0].