Oktalni sistem

Kaj je oktalni sistem?

On Oktalni sistem Gre za osnovni sistem za oštevilčenje osem (8); To pomeni, da je sestavljen iz osem števk, ki so: 0, 1, 2, 3, 4, 5, 6 in 7. Zato ima lahko vsaka številka oktalne številke kakršno koli vrednost od 0 do 7. Oktalne številke se oblikujejo iz binarnih številk.

To je zato, ker je njegova osnova natančna moč (2). To pomeni, da se številke, ki pripadajo oktalnemu sistemu.

Zgodovina oktalnega sistema

Octalni sistem ima svoj izvor v starih časih, ko so ljudje uporabili roke za štetje osem jih je osem živali.

Na primer, da bi v hlevu štelo število krav, je desna roka začela s palcem z majhnim prstom; Nato za štetje druge živali se je palec združil s kazalcem in tako naprej s preostalimi prsti vsake roke, dokler ne dokonča 8.

Obstaja možnost, da sistem oktalnega oštevilčenja pred decimalko lahko šteje interdigitalne prostore; Se pravi, povejte vse prste, razen palcev.

Nato je bil vzpostavljen oktalni sistem oštevilčenja, ki izvira iz binarnega sistema, ker potrebuje veliko števk, da predstavlja samo eno število; Od takrat naprej so bili ustvarjeni oktalni in šesterokotni sistemi, ki ne potrebujejo toliko števk in ki se zlahka pretvorijo v binarni sistem.

Sistem oktalnega oštevilčenja

Oktalni sistem je sestavljen iz osem števk od 0 do 7. Ti imajo enako vrednost kot v primeru decimalnega sistema, vendar se njihova relativna vrednost spremeni, odvisno od položaja, ki ga zasedajo. Vrednost vsakega položaja daje osnovne sile 8.

Lahko vam služi: pravilo T: značilnosti, tako da so primeri

Položaji števk v oktalni številki imajo naslednje pesos:

8⁴, 8³, 8², 8¹, 8⁰, Oktalna točka, 8^-1, 8^-2, 8^-3, 8^-4, 8^-5.

Glavna oktalna številka je 7; Na ta način se, ko se šteje v tem sistemu, položaj številke od 0 do 7 povečuje. Ko doseže 7, se reciklira pri 0 za naslednje štetje; To poveča naslednji številčni položaj. Na primer, če štejemo sekvence, bo v oktalnem sistemu:

• 0, 1, 2, 3, 4, 5, 6, 7, 10.
• 53, 54, 55, 56, 57, 60.
• 375, 376, 377, 400.

Obstaja temeljni teorem, ki se uporablja za oktalni sistem in je izražen na naslednji način:

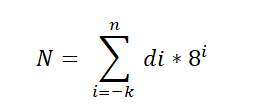
V tem izrazu DI predstavlja številko, pomnoženo z osnovno 8 moči, ki označuje pozicijsko vrednost vsake številke, na enak način, kot je naročen v decimalnem sistemu.

Na primer, imate številko 543.2. Če ga odpeljete v oktalni sistem, se razgradi na naslednji način:

N = ∑ [(5 _* 8²) + (4 _* 8¹) + (3 _*8⁰) + (2 _*8^-1) = (5 * 64) + (4 * 8) + (2 * 1) + (2 * 0.125)

N = 320 +32 + 2 + 0,25 = 354 + 0,25_d

Tako imate 543.2_q = 354.25_d. Naročnina, ki označuje, da gre za oktalno številko, ki jo lahko predstavlja tudi številka 8; in naročnik D se nanaša na decimalno številko, ki jo je mogoče predstaviti tudi s številko 10.

Pretvorba oktalnega sistema v decimalno

Za pretvorbo oktalnega sistema v ekvivalent v decimalni sistem je treba vsako oktonsko številko pomnožiti s svojo pozicijsko vrednostjo, začenši z desnice.

Primer 1

732₈ = (7_* 8²) + (3_* 8¹) + (2_* 8⁰) = (7 _* 64) + (3 _* 8) + (2 _* 1)

732₈= 448 +24 +2

732₈= 474₁₀

Vam lahko služi: matematična enakost

Primer 2

26.9₈ = (2 _*8¹) + (6_* 8⁰) + (9_* 8^-1) = (2 _* 8) + (6 _* 1) + (9 _* 0,125)

26.9₈ = 16 + 6 + 1.125

26.9₈= 23,125₁₀

Pretvorba decimalnega sistema v oktal

Decimalno celo število se lahko pretvori v oktalno številko z metodo ponavljajoče se delitve, kjer je decimalno celo število razdeljeno z 8, dokler količnik ni enak 0, odpadki vsake delitve.

Odpadki se naročijo od zadnjega do prvega; to pomeni, da bo prvi ostanek najmanj pomembna številka oktalnega števila. Na ta način bo najpomembnejša številka zadnji ostanek.

Primer

Oktal decimalne številke 266₁₀

- Decimalna številka 266 je razdeljena na 8 = 266/8 = 33 + 2 ostanka.

- Potem je 33 razdeljen na 8 = 33/8 = 4 + 1 ostanek.

- 4 je razdeljen na 8 = 4/8 = 0 + 4 ostanke.

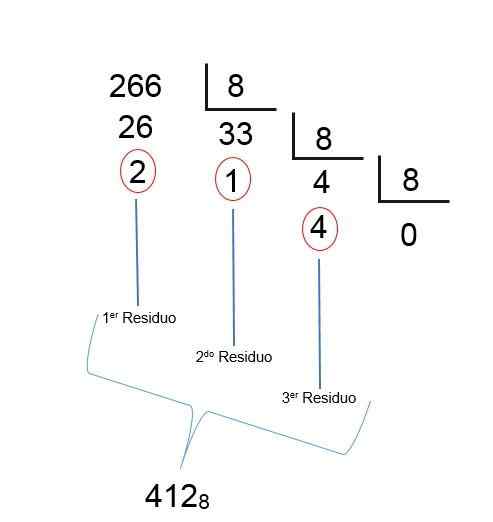
Kot pri zadnjem diviziji je pridobljen količnik A manj kot 1, tudi to pomeni, da je bil rezultat najden; Samo ostanke je treba naročiti vzvratno, tako da je oktalno število decimalnih 266 412, kot je razvidno iz naslednje slike:

Pretvorba binarnega oktalnega sistema

Pretvorba oktalnega v binarni sistem se izvede pri pretvorbi oktalne številke v svojo enakovredno binarno številko, ki jo tvori tri števke. Obstaja tabela, ki prikazuje, kako postane osem možnih števk:

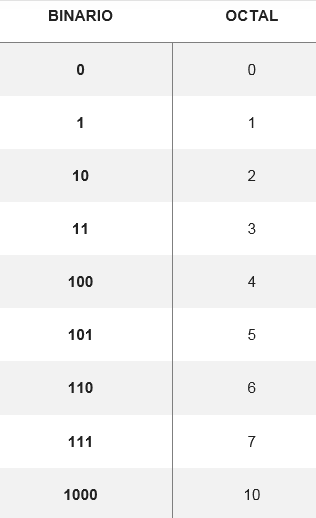
Iz teh konverzij lahko spremenite poljubno število oktalnih sistemov v binarno, na primer pretvorbo številke 572₈ Vaši ustrezniki se iščejo v tabeli. Tako morate:

5₈ = 101

7₈= 111

2₈ = 10

Zato 572₈ enakovredno v binarnem sistemu do 10111110.

Binarni sistem v oktalno pretvorbo

Proces pretvorbe integralnih števil v oktalna cela je obratno delovanje prejšnjega postopka.

Vam lahko služi: kakšni so elementi kota?

To pomeni, da so binarne številčne bite združene v dve skupini treh bitov, začenši od desne proti levi. Nato je iz prejšnje tabele narejena binarna in oktalna pretvorba.

V nekaterih primerih binarno število ne bo imelo skupin 3 bitov; Če ga želite dokončati, se na levo od prve skupine dodata ena ali dva ničla.

Na primer, za spremembo binarne številke 11010110 v oktal je narejeno naslednje:

- Skupine s tremi biti se oblikujejo na desni (zadnji bit):

11010110

- Ker je prva skupina nepopolna, se na levo doda ničla:

011010110

- Pretvorba je narejena iz tabele:

011 = 3

010 = 2

110 = 6

Na ta način je binarna številka 011010110 enakovredna 326₈.

Pretvorba oktalnega sistema v šestnajstično in obratno

Če želite spremeniti oktalno številko v šestnajstični ali šestnajstični v oktalni sistem, je treba, da bo številka najprej binarna, nato.

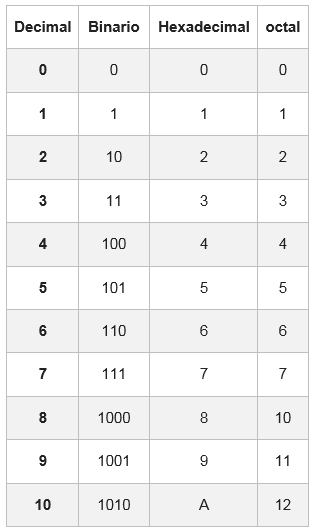
Za to obstaja tabela, v kateri je vsaka šestnajstična številka predstavljena s svojo enakovrednostjo v binarnem sistemu, sestavljena iz štirih števk.

V nekaterih primerih binarno število ne bo imelo skupin 4 bitov; Če ga želite dokončati, se na levo od prve skupine dodata ena ali dva ničla

Primer

Pretvorite 1646 oktalno številko v šestnajstično številko:

- Oktalno do binarno število postane

1₈ = 1

6₈ = 110

4₈ = 100

6₈ = 110

- Tako, 1646₈ = 1110100110.

- Za pretvorbo iz binarne v šestnajstično so se najprej naročili v skupini 4 bitov, začenši od desne na levi:

11 1010 0110

- Prva skupina je dokončana z ničli, tako da ima lahko 4 bite:

0011 1010 0110

- Izdelana je še heksadecimalna pretvorba binarnega sistema. Enakovrednosti se nadomestijo s tabelo:

0011 = 3

1010 = a

0110 = 6

Na ta način je oktalna številka 1646 enakovredna 3A6 v šestnajstičnem sistemu.