Matematika

Pravokotni koordinatni sistem

Pravokotni koordinatni sistem
Kartezijanski koordinatni sistem v treh dimenzijah. Vir: Wikimedia Commons

Kakšen je pravokotni koordinatni sistem?

V matematiki in geometriji, a Pravokotni koordinatni sistem Služi za natančno iskanje katere koli točke na prostoru. Za to je dovolj, da damo tri koordinate.

Konstrukcija sistema v ravnini je zelo preprosta, potrebne so le tri črte, ki bodo koordinatne osi ali kartezijanske osi: ena navpična, druga vodoravna in tretjina, ki vstopi ali zapusti papir ali zaslon.

Te osi so medsebojno pravokotne, presečišče izvor sistema.

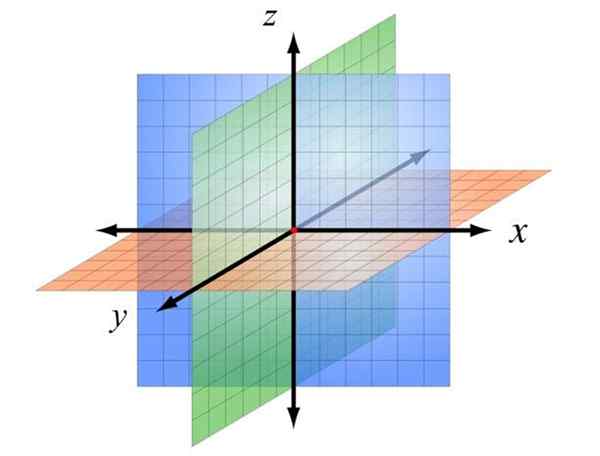
Ta določba je prikazana na zgornji sliki, v kateri so črke dodeljene črki x, in, z, da jih ločimo. Na ta način so določena tri letala, izvor je obarvan v rdeči barvi.

Ravnina Xz, V modrem je ravnina zaslona in je pred bralčevim očmi. Ravnina Xy Je oranžna in je lahko povezana z mizo ali tlemi. Končno letalo zy V zeleni barvi je pravokotno na prejšnje in razsežete zaslon ali papir v dveh regijah.

Quadriculing vsake od teh ravnin in dodeljevanje lestvice lahko postavite katero koli točko v prostoru, ki daje ustrezne koordinate X in z, Vedno v tem vrstnem redu, da se izognemo dvoumnostim.

Za kajSluži pravokotni koordinatni sistem?

Pravokotni koordinatni sistem služi za namestitev katere koli točke v prostoru ali v ravnini, dovolj, da označi tri koordinate točke, po vrstnem redu x, y, z.

Lahko vam služi: nominalna spremenljivka: koncept in primeri

Če točka pripada ravnini, bo ena od koordinat 0 in če je na kateri koli od osi, bosta dve koordinati 0, razen tiste, ki ustreza lokaciji točke je že rekel, ima koordinate (0,0,0).

Naslednji primeri razjasnijo zgoraj.

Primeri

Primer 1

Vsaka točka p na osi x se izraža s koordinatami P (x, 0, 0). Upoštevajte, da ima izvor, poudarjen z rdečo barvo na naslednji sliki, koordinate ali (0, 0, 0).

Ko je točka desno od izvora, ima pozitivno koordinato X, medtem ko je na levi strani, je negativna. Na primer, P1 Blue Point ima koordinate (6,0,0), medtem ko točka P2 v zeleni koordinat (-9,0,0).

Primer 2

Na naslednji sliki sta dve osi, ki sta Os x vodoravna os in Os y Navpično. S tem je dovolj, da predstavljate točke v letalu, dve koordinati sta potrebni. Izvor ali je točka (0,0).

Upoštevajte, da razporeditev osi razdeli ravnino na štiri regije, imenovane kvadranti. Osi zgoraj in desno od izvora so označene s pozitivnim znakom, na levi strani pa se razlikujejo z negativnim znakom.

Nato točke, katerih koordinate so pozitivne, ustrezajo prvemu kvadrantu ali kvadrantu. Zelena točka ima koordinate (2,3) in je v kvadrantu I.

Rdeča točka ima koordinate (-3,1) in je v kvadrantu II, medtem ko so koordinate modre točke (-1.5; -2.5) in je v kvadrantu III.

Vam lahko služi: Skupna faktorizacija: primeri in vaje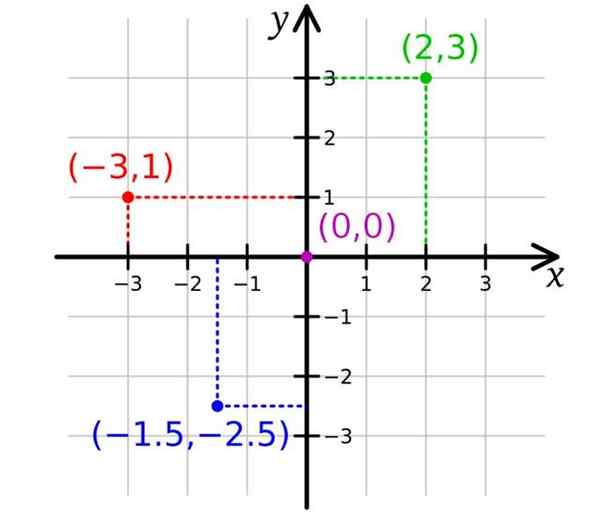 Kartezijansko letalo. Vir: Wikimedia Commons

Primer 3

Sledi primer točke v vesolju. Njegove koordinate so x = 6, y = 10 in z = 8, torej p (6,10,8).

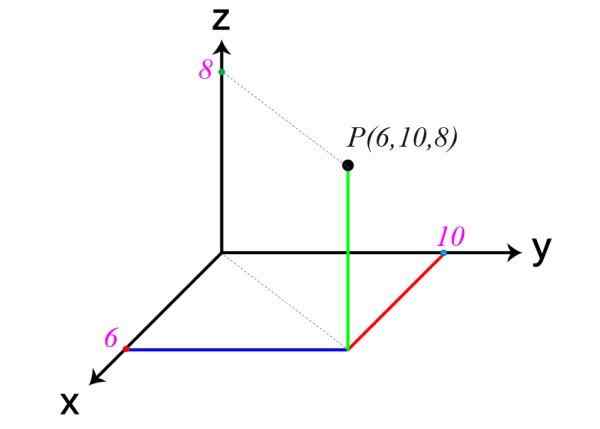Še en primer kartezijanskih osi

Na sliki začetka je opozorjeno, da načrti XY, XZ in Zy razdelijo prostor na osem regij, imenovanih Oktaverji. Točka P primera je v prvem ocantu.

Reference

  1. Aleksander, d. (2013). Geometrija. 5. Izdaja. Cengage učenje.
  2. Larson, r. (2012). Prekalenkulacija. 8. Izdaja. Cengage učenje.
  3. Stewart, J. (2007). Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.
  4. Kartezijansko letalo. Pridobljeno iz: dl.UNCW.Edu.
  5. Weisstein, e. Kartezijanske koordinate. Okreval od: Mathworld.Wolfram.com