Simpson pravila Formula, demonstracija, primeri, vaje

The Pravilo Simpsona To je metoda za izračun približno definiranih integralov. Temelji na delitvi integracijskega intervala na par pod-intervalov, enako razmaknjenih.

Ekstremne vrednosti dveh zaporednih pod-intervalov določajo tri točke, ki prilagodi parabolo, katere enačba je polinom druge stopnje. 

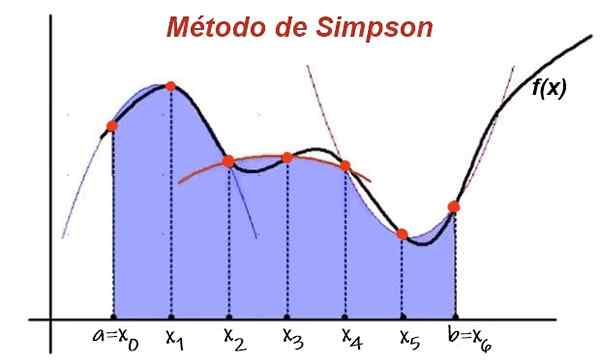
Slika 1. V metodi Simpson je interval integracije razdeljen na par intervalov enake širine. Funkcija je približno prispodoba v vsaki 2 pododstalos in integralni pristopi z vsoto območja pod prispodobami. Vir: UPV.je.

Nato je območje pod krivuljo funkcije v dveh zaporednih intervalih približeno s pomočjo interpolacijske polinomne površine. Če dodate prispevek na območje pod prispodobo o vseh zaporednih pododdelkih, obstaja približno vrednost integrala.

Po drugi strani pa je, ker lahko integral prispodobe izračunamo algebraično natančno, potem je mogoče najti analitično formulo za približno vrednost definiranega integrala. Je znan kot Simpsonova formula.

Tako pridobljena napaka pri približnem rezultatu se zmanjšuje do te mere, da je število pododdelkov n večje (n a n a navor) število.

Spodaj bo podan izraz, ki omogoča oceno zgornje stopnje napake pristopa na integral I, ko je bila narejena particija rednih podtemnikov celotnega intervala [A, B] [B].

[TOC]

Formula

Interval integracije [a, b] je razdeljen na n podintrale, pri čemer je n navora. Širina vsakega oddelka bo:

H = (b - a)/n

Na ta način je v intervalu [a, b] izdelana particija:

X0, x1, x2, ..., xn-1, xn

Biti x0 = a, x1 = x0 + h, x2 = x0 + 2H,…, xn-1 = x0 + (n-1) h, xn = x0 + nh = b.

Lahko vam služi: razlika med krogom in obodom (s primeri)

Formula, ki omogoča približno izračun definirane integralne in neprekinjene funkcije in po možnosti mehka, v intervalu [a, b] je:

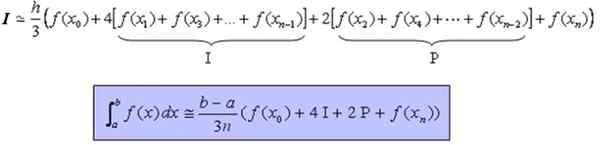
Demonstracija

Če želite pridobiti simpsonovo formulo, se v vsakem podintervalu [xi, xi+2] funkcija f (x) približa s polinomom druge stopnje p (x) (prispodoba), ki poteka skozi tri točke: [xi, f (f (f (f (f (F (F (F (F (F (F (F (F (F (F (F Xi)]; [Xi+1, f (xi+1)] in [xi+2, f (xi+2)]].

Nato se v [xi, xi+2] izračuna integralni polinomni p (x), ki v tem intervalu približa integralu funkcije f (x).

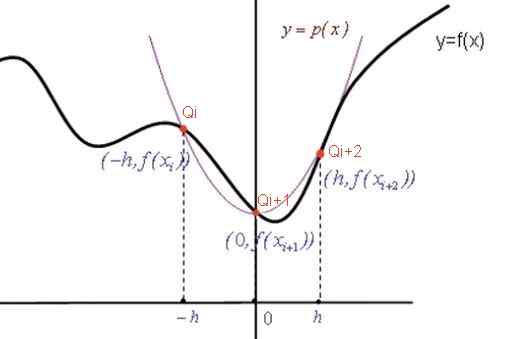Slika 2. Graf za prikaz simpsonove formule. Vir: f. Zapata.

Interpolacijski polinomni koeficienti

Enačba parabole p (x) ima splošno obliko: p (x) = a x² + B x + c. Ko prispodoba gre skozi točke, ki so navedene v rdeči barvi (glej sliko), se koeficienti A, B, C določijo iz naslednjega sistema enačb:

A (-H)² - B H + C = F (xi)

C = F (xi+1)

A (h)² + B H + C = F (xi + 2)

Lahko opazimo, da se določi koeficient c. Za določitev koeficienta dodamo prvo in tretjo enačbo, ki dobimo:

2 a h² + 2 c = f (xi) + f (xi + 2).

Potem je vrednost C zamenjana in jasna je:

A = [f (xi) - 2 f (xi+1)+f (xi+2)] / (2 h²)

Za določitev koeficienta B se odšteje tretja enačba prvega in B se razjasni:

B = [f (xi+2) - f (xi)] = 2 h.

Če povzamemo, ima polinomni polinom P (x), ki poteka skozi točke Qi, Qi+1 in Qi+2, koeficiente:

A = [f (xi) - 2 f (xi+1)+f (xi+2)] / (2 h²)

B = [f (xi+2) - f (xi)] = 2 h

C = F (xi+1)

Izračun približnega integrala v [xi, xi+2]

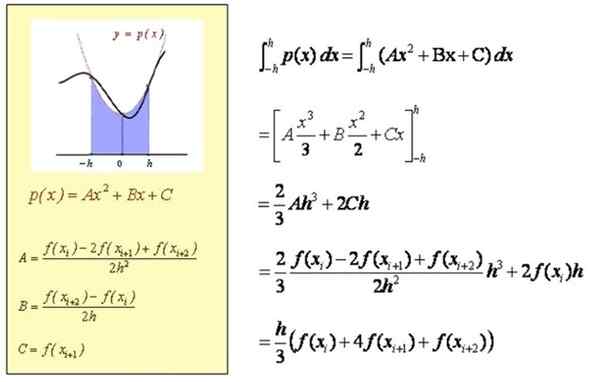
Približen izračun integrala v [a, b]

Kot je že bilo rečeno, v skupnem intervalu integracije [a, b] a particija x0, x1, x2,…, xn -1, xn s korakom h = xi+1 - xi = (b - (b -) / n, kjer je n par.

Lahko vam služi: Napaka vzorčenja: formule in enačbe, izračun, primeri

Potem je integral, opredeljen v skupnem intervalu [a, b], vsota integralov v podintralih [xi, xi+2], ki se jim približajo integrali interpolacijskih polinomov p (x):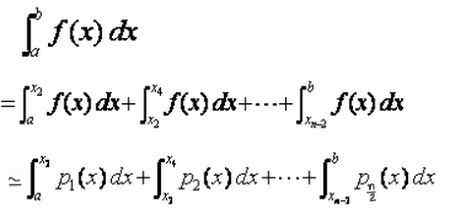

V prejšnjem razdelku so našli formulo za polinomne integrale v podintralih. Uporaba tega rezultata za vsak integral ima: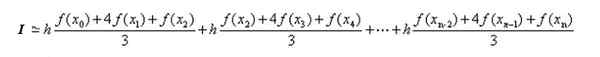

Ki jih je mogoče napisati na bolj kompakten način: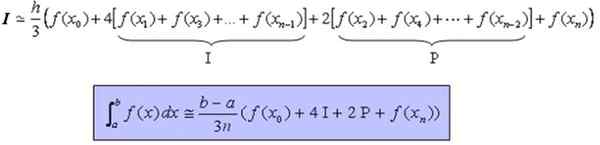

Napaka pristopa

Če je funkcija, v katero se želite vključiti v interval [a, b], izpeljala v četrti vrstni red, v tem intervalu neprekinjena, potem je mogoče najti formulo, ki omogoča določitev največje stopnje napake v pristopu s sredstvi od Formula Simpson SN Za vrednost integrala: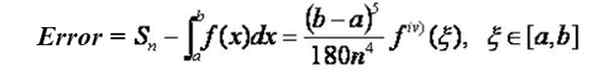

Upoštevajte, da se napaka zmanjšuje s četrto močjo števila intervalnih pododdelkov. Na primer, če greste od n pododdelkov na 2N, se napaka zmanjša za faktor 1/16.

Zgornjo stopnjo napak, ki jo dobimo s Simpsonovim pristopom, je mogoče dobiti iz te iste formule, pri čemer je četrti derivat nadomeščen z največjo absolutno vrednostjo četrtega derivata v intervalu [a, b].

Rešeni primeri

- Primer 1

Razmislite o funkciji f (x) = 1 / (1 + x²). 

Poiščite definirani integral funkcije f (x) v intervalu [-1, 1] z uporabo metode Simpson z dvema pododdelkoma (n = 2).

Rešitev 

Je vzet n = 2. Omejitve integracije so A = -1 in B = -2, potem je particija takšna: 

X0 = -1; X1 = 0 in x2 = +1.

Zato Simpsonova formula sprejema na naslednji način:

Z n = 2 → xo = -1, x1 = 0; x2 = 1, torej:

- Primer 2

Razmislite o funkciji f (x) = 1 / (1 + x²). 

Poiščite definirani integral funkcije f (x) v intervalu [-1, 1] s simpsonovo formulo s štirimi pododdelki (n = 4).

Lahko vam služi: ocena po presledkih

Rešitev 

Je vzet n = 4. Omejitve integracije so A = -1 in B = -2, potem je particija takšna: 

X0 = -1; X1 = -1/2; X2 = 0; X3 = 1/2 in x4 = +1.

Simpsonova formula je vzpostavljena na naslednji način:

Integral ≃ [(b -a)/(3 n)] [f (x0) + 4 i + 2 p + f (xn)]

Za primer, v katerem se uporablja, je naslednji:

Integral ≃ (1- (1))/(3⋅4)] [f (-1) + 4 [f (-½) + f (½)] + 2 [f (0)] + f (1)

Integral ≃ (2/12) [½ + 4 (⅘ + ⅘) + 2⋅1 + ½] = (⅙) [47/5] = 47/30 = 1.5666

- Primer 3

Natančno določite definiran integral prejšnjih primerov in primerjajte natančen rezultat s tistimi, ki jih je v primerih 1a in 1b pridobil Simpsonovo formulo.

Rešitev 

Nedoločen integral funkcije f (x) = 1 / (1 + x²) je funkcija Arctan (x).

Pri ocenjevanju omejitev integracije:

Integral = arctan (1) - arctan (-1) = π/4 - (-π/4) = π/2 = 1,5708

Če primerjamo rezultat natančne rešitve s tisto, ki jo dobimo z metodo Simpson z n = 2 in n = 4, imamo:

Za n = 2 je razlika med natančno in približno rešitev π/2 -5/3 = -0959, torej odstotna razlika v -0,06%.

Za Simpsonovo pristop z n = 4 je razlika med natančno in približno rešitev π/2 - 47/30 = 0,0041, torej odstotna razlika 0,003%.

Predlagana vaja

Simpsonova metoda je primerna za uporabo v programskih jezikih in računalniških aplikacijah, namenjenih matematičnim izračunom. Bralcu je predlagano, ki na podlagi formul, navedenih v tem članku, napiše svojo kodo v svojem najljubšem programu.

Naslednja slika prikazuje vajo, v kateri je bila izvedena simpsonova formula STATH STUDIO, Brezplačna programska oprema, ki je na voljo za operacijske sisteme Okna in Android.

Slika 3. Primer numerične integracije s pomočjo pravila Simpson z uporabo programske opreme. Vir: f. Zapata.

Reference

1. Casteleiro, J. M. 2002. Celovit izračun (ilustrirana izdaja). Madrid: uredništvo ESIC.
2. UPV. Metoda Simpson. Politehnična univerza v Valenciji. Obnovil od: YouTube.com
3. Purcell, e. 2007. Izračun devete izdaje. Dvorana Prentice.
4. Wikipedija. Pravilo Simpsona. Okrevano od: je.Wikipedija.com
5. Wikipedija. Polinomska interpolacija LaGrange. Okrevano od: je.Wikipedija.com