Pravilo desnega roka

Slika 1. Pravilo desnega roka. Vir: Wikimedia Commons. ACDX [CC By-S (http: // creativecommons.Org/licence/by-sa/3.0/]].

Kaj je pravilo desne roke?

The pravilo desnega roka To je mnemonični vir za določitev smeri in smeri vektorja, ki je posledica vektorskega izdelka ali navzkrižnega izdelka. V fiziki se pogosto uporablja, saj obstajajo pomembne vektorske velikosti, ki so posledica vektorskega izdelka. Takšen je primer navora, magnetne sile, kotnega zagona in magnetnega trenutka.

Biti dva generična vektorja do in b čigar križni izdelek je do x b. Modul takšnega vektorja je:

do x b = do.b.greh α

Kjer je α najmanjši kot med do in b, Medtem ko A in B predstavljata svoje module. Za razlikovanje vektorjev od svojih modulov se uporabljajo drzne črke.

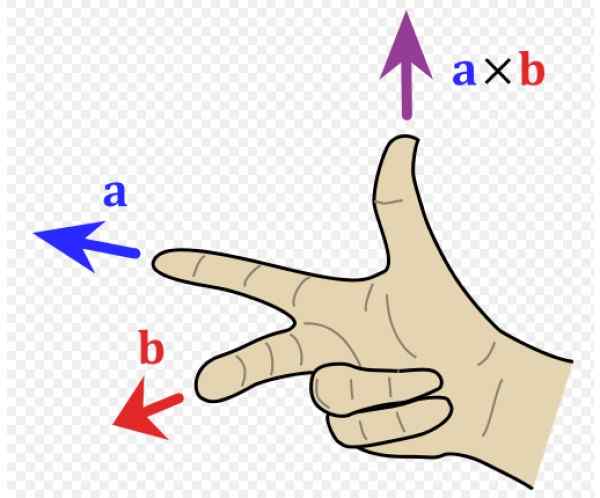
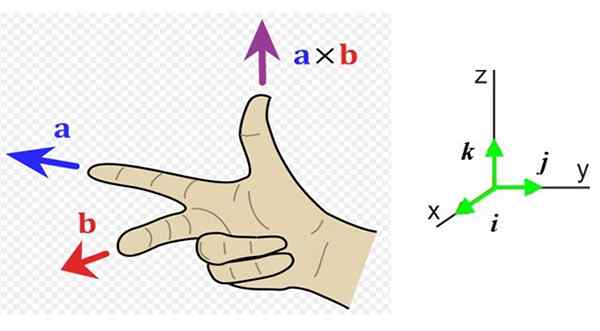
Zdaj moramo vedeti smer in pomen tega vektorja, zato je priročno imeti referenčni sistem s tremi smeri prostora (slika 1 desno). Vektorji enot Yo, J in k Kažejo na bralca (zunaj strani), desno in navzgor.

V primeru slike 1 levo vektor do gre na levo (naslov in negativni in kazalec desne roke) in vektor b gre k bralcu (naslov x pozitiven, srednji prst desne roke).

Nastali vektor do x b ima smer palca, navzgor v smer z pozitivno.

Drugo pravilo desne roke

To pravilo se veliko uporablja, kadar obstajajo veličini, katerih smer in pomen se vrtijo, na primer magnetno polje B proizveden s tanko in pravokotno žico, ki prevaža tok.

V tem primeru so linije magnetnega polja koncentrični obod z žico, smer obrata pa s tem pravilom dobimo na naslednji način: desni palec označuje smer toka, preostali štirje prsti pa so ukrivljeni v smeri v smeri smer polja. Ponazorimo koncept na sliki 2.

Vam lahko služi: elastični pretresi: v dimenziji, posebni primeri, vaje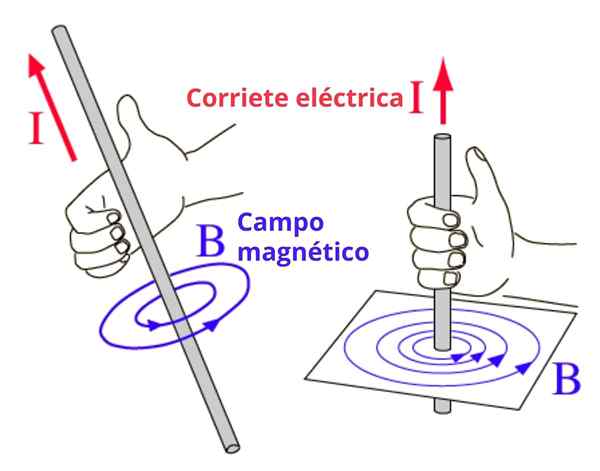Slika 2. Pravilo desnega ročnega za določitev pomena kroženja magnetnega polja

Alternativno pravilo desne roke

Naslednja slika prikazuje alternativno obliko desnega pravila. Vektorji, ki se pojavijo v razsvetljenstvu, so:

• Hitrost v točnega obremenitve.
• Magnetno polje B znotraj katere se obremenitev premika.
• F_B Sila, ki jo na obremenitvi izvaja magnetno polje.

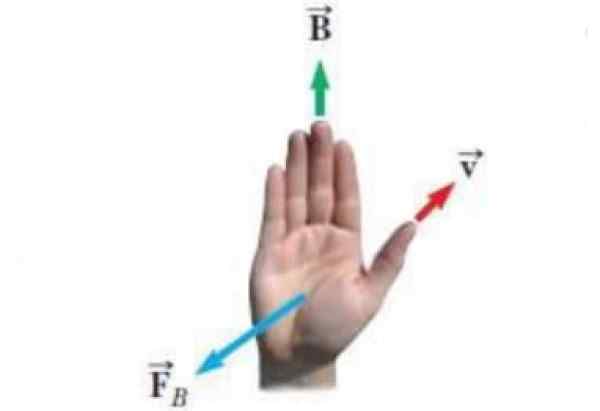Slika 3. Alternativno pravilo desne roke. Vir: Wikimedia Commons. ExpertIcUis [CC BY-SA (https: // createCommons.Org/licence/by-sa/4.0)]

Enačba za magnetno silo je F_B = qv x B in pravilo desne roke, da spoznate smer in občutek F_B Uporablja se takole: točke palca Po V, preostali štirje prsti so nameščeni v skladu s poljem B. Tako F_B To je vektor, ki izhaja iz dlanine, pravokotno nanjo, kot da bi si pritiskal na obremenitev.

Upoštevajte to F_B bi pokazal v nasprotno smer, če bi bila obremenitev negativna, saj vektorski izdelek ni komutativen. Pravzaprav:

do x B = - b x do

Prijave

Pravilo desne roke se lahko uporabi za različne fizične velikosti, nekaj pa jih poznamo:

Kotna hitrost in pospešek

Obe kotni hitrosti Ω Kot kotni pospešek α So vektorji. Če se predmet vrti okoli fiksne osi, je možna kotna hitrost Ω.

Kotni pospešek α bo imel isti naslov kot Ω, Toda njegov pomen je odvisen od tega, ali Ω povečuje ali zmanjšuje svojo velikost sčasoma. V prvem primeru imata oba isto smer in pomen, v drugem pa bo imela nasprotna čutila.

Vam lahko služi: Watt Law: kaj je, primeri, prijave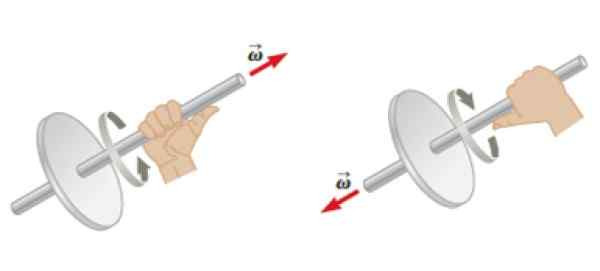Slika 4. Pravilo desne roke, ki se uporablja za objekt v vrtenju, za določitev smeri in smeri kotne hitrosti. Vir: Serway, r. Fizično.

Kotni zagon

Kotni vektor L_Tudi delca, ki se vrti okoli določene osi ali je opredeljen kot vektorski produkt njegovega vektorja r  in količino linearnega gibanja str:

L = r x str

Na ta način se uporablja pravilo desnega inhand: kazalec je nameščen v isto smer in smer r, Srednji prst v str, oba na vodoravni ravnini, kot na sliki. Samodejno se palec razteza navpično navzgor, kar kaže na smer in smer kotnega trenutka L_Tudi.

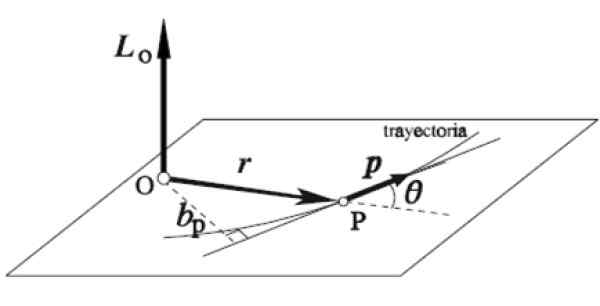Slika 5. Kotni vektor. Vir: Wikimedia Commons.

Vaje

Vaja 1

Spin slike 6 gre hitro z kotno hitrostjo Ω in njegova os simetrije se počasneje lomi okoli navpične osi z. To gibanje se imenuje precesija. Opišite sile, ki delujejo na vrtenje in učinek, ki ga prinašajo.

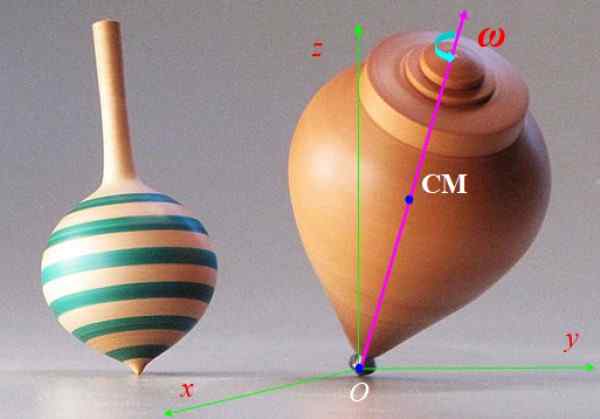Slika 6. Spinning Spin. Vir: Wikimedia Commons.

Rešitev

Sile, ki delujejo na vrtenje, so normalne N, Uporablja se na podporni točki s tlemi ali več teže mg, uporabljen v središču mase CM, z g Vektor pospeševanja resnosti, usmerjen navpično navzdol (glej sliko 7).

Obe sili sta uravnoteženi, zato se spin ne premika. Vendar teža ustvari navor ali navor τ Neto o točki ali, ki jo daje:

τ_Tudi = r_Tudi x F, z F = Mg.

Kot r in mg Vedno so na ravnini, ko se vrtenje obrača, glede na pravilo desne roke navora τ_Tudi Vedno se nahaja v letalu Xy, pravokotno oba a r kot g.

Upoštevajte to N ne daje navora glede na O, ker njegov vektor r Glede ali je NULL. Ta navor povzroči spremembo kotnega zagona, ki povzroči precesijo vrtenja okoli osi z.

Vam lahko služi: termodinamično ravnovesje: razredi in aplikacije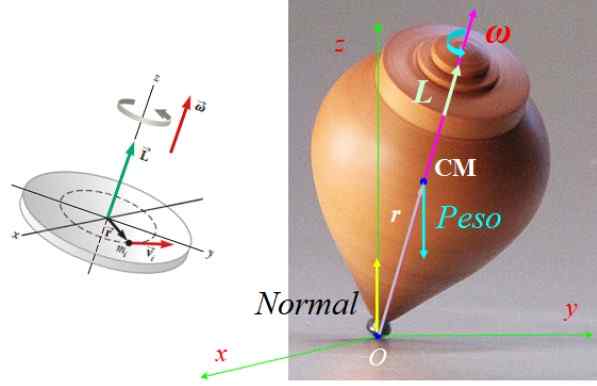Slika 7. Sile, ki delujejo na vrtenje in njegov kotni vektor. Vir leve slike: Serway, r. Fizika za znanost in inženiring.

Vaja 2

Izpostavite smer in smer vektorja kotnega trenutka L Trumpeja slike 6.

Rešitev

Vsaka točka vrtenja ima maso m_Yo, hitrost v_Yo in položaj vektor r_Yo, Ko se vrti okoli osi z. Kotni zagon L_Yo omenjenega delca je:

L_Yo = r_Yo x str_Yo = r_Yo x m_Yov_Yo

Glede na r_Yo in v_Yo So pravokotne, velikost L je:

L_Yo = m_Yor_Yov_Yo

Linearna hitrost v je povezan z kotno hitrostjo Ω skozi:

v_Yo = r_YoΩ

Zato:

L_Yo = m_Yor_Yo (r_YoΩ) = m_Yor_Yo²Ω

Skupni kotni zagon Trompo L je vsota kotnega zagona vsakega delca:

L = (∑m_Yor_Yo² ) Ω

∑ m_Yor_Yo²  Nato je trenutek inercije I Spin, potem pa:

L= IΩ

Zato L in Ω Imajo isto smer in pomen, kot je prikazano na sliki 7.