Zmanjšanje podobnih izrazov

Kakšno je zmanjšanje podobnih izrazov?

The zmanjšanje podobnih izrazov Gre za metodo, ki se uporablja za poenostavitev algebrskih izrazov. V algebrskem izrazu so podobni izrazi tisti, ki imajo enako spremenljivko; to pomeni, da imajo enake neznanke, ki jih predstavlja pismo, in imajo enake eksponente.

V nekaterih primerih so polinomi obsežni in za dosego rešitve morate poskusiti zmanjšati izraz; To je mogoče, kadar so podobni izrazi, ki jih je mogoče kombinirati z uporabo algebrskih operacij in lastnosti, kot so vsota, odštevanje, množenje in delitev.

Pojasnilo

Podobne izraze tvorijo enake spremenljivke z istimi eksponenti, v nekaterih primerih pa se razlikujejo le po njihovih numeričnih koeficientih.

Tisti, ki nimajo spremenljivk, veljajo tudi za podobne izraze; torej tisti izrazi, ki imajo samo konstante. Tako so na primer naslednji podobni izrazi:

• 6x² - 3x². Oba izraza imata enako spremenljivko x².
• 4²b³ + 2. mesto²b³. Oba izraza imata enake spremenljivke²b³.
• 7 - 6. Izrazi so konstantni.

Tisti izrazi, ki imajo enake spremenljivke, vendar z različnimi eksponenti imenujemo ne -podobni izrazi, kot so:

• 9²B + 5AB. Spremenljivke imajo različne eksponente.
• 5x + in. Spremenljivke so različne.
• B - 8. En izraz ima spremenljivko, drugi je konstanta.

Prepoznavanje podobnih izrazov, ki tvorijo polinom. Na ta način je izraz poenostavljen z zmanjšanjem števila izrazov, ki ga sestavljajo, in izračun njene rešitve olajša.

Kako zmanjšati podobne izraze?

Zmanjšanje podobnih izrazov se izvede z uporabo asociativne lastnosti dodajanja in distribucijske lastnosti izdelka. Z naslednjim postopkom je mogoče znižati izraze:

• Prvič, podobni izrazi so združeni.
• Koeficienti (številke, ki spremljajo spremenljivke) podobnih izrazov, se dodajo ali odštejejo, uporabijo se asociativne, komutativne ali distribucijske lastnosti, kot je primer.
• Nato se zapišejo novi pridobljeni pogoji, ki pred njimi postavijo znak, ki je posledica operacije.

Vam lahko služi: diskretna matematika

Primer

Zmanjšajte pogoje naslednjega izraza: 10x + 3y + 4x + 5y.

Rešitev

Najprej se pogoji naročijo, da združijo podobne, pri uporabi komutativne lastnosti:

10x + 3y + 4x + 5y = 10x + 4x + 3y + 5y.

Nato se uporabi distribucijska lastnost in dodajo koeficienti, ki spremljajo spremenljivke, da se doseže zmanjšanje izrazov:

10x + 4x + 3y + 5y

= (10 + 4) x + (3 + 5) in

= 14x + 8y.

Za zmanjšanje podobnih izrazov je pomembno upoštevati znake, ki imajo koeficiente, ki spremljajo spremenljivko. Obstajajo trije možni primeri:

Zmanjšanje podobnih izrazov z enakimi znaki

V tem primeru se dodajo koeficienti in pred rezultatom postavimo znak izrazov. Če so pozitivni, bodo dobljeni izrazi pozitivni; V primeru, da so izrazi negativni, bo rezultat imel znak (-), ki ga spremlja spremenljivka. Na primer:

a) 22ab² + 12AB² = 34 AB².

b) -18x³ - 9x³ - 6 = -27x³ - 6.

Zmanjšanje podobnih izrazov cNa različnih znakih

V tem primeru se koeficienti odštejejo in pred rezultatom postavimo znak glavnega koeficienta. Na primer:

a) 15x²in - 4x²in + 6x²in - 11x²in

= (15x²in + 6x²Y) + ( - 4x²in - 11x²in)

= 21x²Y + (-15x²in)

= 21x²in - 15x²in

= 6x²in.

b) -5a³B + 3 a³B - 4a³b + a³b

= (3 a³b + a³b) + (-5a³B - 4a³B

= 4a³B - 9a³b

= -5 a³b.

Na ta način se za zmanjšanje podobnih izrazov z različnimi znaki oblikuje en sam aditivni izraz z vsemi tistimi, ki imajo pozitiven znak (+), koeficienti dodajo in rezultat spremljajo spremenljivke.

Lahko vam služi: enotni krog: trigonometrične funkcije in aplikacije

Na enak način se oblikuje odšteti izraz, z vsemi tistimi izrazi, ki imajo negativni znak (-), se dodajo koeficienti in rezultat spremljajo spremenljivke.

Nazadnje se odštejejo vsote obeh izrazov in znak največjega je postavljen na rezultat.

Zmanjšanje podobnih izrazov v operacijah

Zmanjšanje podobnih izrazov je operacija algebre, ki jo je mogoče uporabiti v delitvi, odštevanje, množenje in algebrsko delitev.

V vsotah

Ko imate več polinomov s podobnimi izrazi, da jih zmanjšate, se pogoji vsakega polinoma naročijo, da držijo znake, potem so napisani po drugih in podobni izrazi se zmanjšajo. Na primer, imate naslednje polinome:

3x - 4xy + 7x²in + 5xy².

- 6x²in - 2xy + 9 xy² - 8x.

V odštevanju

Če želite odšteti polinom iz drugega, se Minuend napiše in nato odšteje s spremenjenimi znaki, nato pa se zmanjša zmanjšanje podobnih izrazov. Na primer:

5³ - 3ab² + 3b²c

6AB² + 2. mesto³ - 8b²c

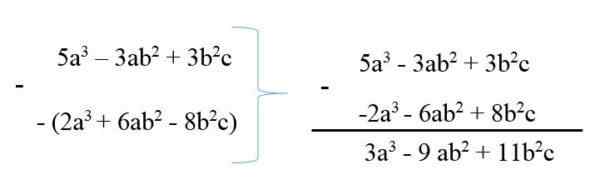
Tako se polinomi povzamejo na 3a³ - 9AB² + 11b²c.

Pri množenju

V polinomskem izdelku izrazi, ki sestavljajo množenje za vsak izraz, ki tvori množitelj, če upoštevamo, da znaki množenja ostajajo enaki, če so pozitivni, če so pozitivni.

Spremenjeni bodo le, ko se pomnožijo z negativnim izrazom; Torej, ko bosta dva izraza istega znaka pomnožila rezultat pozitiven (+), in ko imata različne znake, bo rezultat negativen (-).

Na primer:

a) (a + b) _* (A + B)

= a² + AB + AB + B²

= a² + 2ab+ b².

b) (a + b) _* (A - B)

= a² - AB + AB - B²

= a² - b².

c) (a - b) _* (A - B)

= a² - AB - AB + B²

= a² - 2ab+ b².

V oddelkih

Ko želite zmanjšati dva polinoma skozi divizijo, mora tretji polinom.

Lahko vam služi: Tukey Test: Kaj je v primeru, da je v primeru rešena vaja

Za to je treba določiti pogoje dividende in deličarja od leve proti desni, tako da so spremenljivke v obeh v istem vrstnem redu.

Oddelek se nato izvede, začenši z prvega mandata leve dividende med prvo na levi strani delitve, ki vedno upošteva znake vsakega mandata.

Na primer, zmanjšajte polinom: 10x⁴ - 48x³in + 51x²in² + 4xy³ - 15y⁴ delitev med polinom: -5x² + 4xy + 3y².

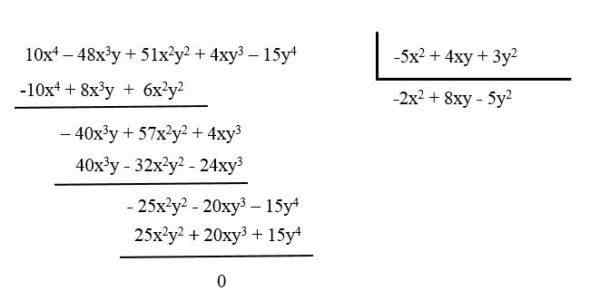
Nastali polinom je -2x² + 8xy - 5y².

Rešene vaje

Prva vaja

Zmanjšajte pogoje algebrskega izraza:

15A² - 8AB + 6A² - 6AB - 9 +4A² - 13 ab.

Rešitev

Uporabljena je komutativna lastnost vsote, ki razvršča izraze, ki imajo enake spremenljivke:

15A² - 8AB + 6A² - 6AB + 9 + 4A² - 13

= (15a² + 6² + 4²) + ( - 8AB - 6AB) + (9 - 13).

Nato se uporabi distribucijska lastnost množenja:

15A² - 8AB + 6A² - 6AB + 9 + 4A² - 13

= (15 + 6 + 4) a² + ( - 8 - 6) AB + (9 - 13).

Končno jih poenostavimo z dodajanjem in odštevanjem koeficientov vsakega izraza:

15A² - 8AB + 6A² - 6AB + 9 + 4A² - 13

= 25A² - 14AB - 4.

Druga vaja

Poenostavite izdelek naslednjih polinomov:

(8x³ + 7xy²)_*(8x³ - 7 xy²).

Rešitev

Vsak izraz prvega polinoma se pomnoži z drugim, ob upoštevanju, da so znaki izrazov različni; Zato bo rezultat njegovega množenja negativen, prav tako pa je treba uporabiti zakone eksponentov.

(8x³ + 7xy²) _* (8x³ - 7xy²)

= 64 x⁶ - 56 x³_* Xy² + 56 x³_* Xy² - 49 x²in⁴

= 64 x⁶ - 49 x²in⁴.