Razlog za spremembo

Kaj je razlog za spremembe?

The razlog za spremembo Prav matematična velikost določa spremembo spremenljivke ali fizične velikosti glede drugega. Na primer, hitrost je razlog za spremembo položaja glede na čas.

Sprememba obsega x, Označena je z grškim besedilom Δ (bere se "Delta") in je napisana Δx. Izračuna se z razliko med končno in začetno vrednostjo: Δx = x_finale- x_začetno.

Če velikost x je povezan z drugo velikostjo in, To doživi tudi spremembo, imenovano Δy = y_finale- in_začetno, Razlog za spremembo y glede na X je opredeljen kot količnik:

Ki, z uporabo zapisa z Delta, ki je bila navedena prej, ostaja taka:

Ta količnik je znan kot Povečati količnik od in s spoštovanjem do x tudi Povprečno ali povprečno razmerje sprememb.

Na ta način lahko opredelite velikosti, kot so indeks rasti populacije, hitrost, s katero predmet, stopnja brezposelnosti, voda teče skozi cev in še veliko več. Vsi ti zneski so dejansko razlogi za spremembe.

Zakaj je pomembno izračunati razlog za spremembe?

Številne velikosti, ki jih zanimajo, ne ostajajo nespremenljive, vendar se doživljajo spremembe in pogosto te spremembe sledijo med seboj pravočasno. Od tod tudi pomen izračuna razloga za spreminjanje obsega sčasoma.

Na primer, obstaja preprost primer predmeta, ki se premika po ravni črti, ki je lahko vodoravna os ali os x. Mobilni telefon (avtomobil, kolo, oseba, ki hodi ali teče ...) nenehno spreminja svoj položaj, ko čas mineva t.

Nato je razlog za spremembo položaja predmeta Δx v časovnem intervalu ΔT znan kot povprečna hitrost:

Drug mobilni telefon, ki potuje po isti ravni črti, lahko to stori z drugačno hitrostjo, bodisi manj, in na ta način se razlikuje od prvega mobilnega telefona (ker je počasnejši ali hitrejši).

Na primer, 100 -metrski ravni koridor bo imel povprečni menjalni tečaj v svojem položaju, ki je veliko večji od maratonerja ali osebe, ki tiho hodi po ulici.

Hitrost je značilen primer razmerja med spremembami, vendar nekaj zanimivih velikosti, ki prav tako doživljajo spremembe v času, so: temperatura, prostornina tekočine, električni naboj, populacija bakterij in še veliko več.

Če poznate svoj razlog za spremembe, lahko veliko veste o načinu, kako se te velikosti razvijajo sčasoma.

Enote razloga za spremembe

Razmerje je razmerje med dvema velikosti, posledične enote pa bodo tudi količnik enot, ki se uporabljajo za njihovo merjenje. Na primer, hitrost je dolžina med časom, saj je razlog za spremembo položaja glede na čas.

Na ta način so lahko hitrostne enote metri/sekunde, kilometri/uro, milje/uro in številne druge kombinacije.

Kako se izračuna razlog za spremembo?

Povprečni razlog ali menjalni tečaj med dvema velikosti se zlahka izračuna pri izvajanju količnika med ustreznimi variacijami vsakega v skladu s formulo:

Spremembe v magnetudah lahko damo s tabelami zalog ali jih določimo z grafom, od katerih ustrezne vrednosti in in x (Glej vaje, rešene na koncu).

Po drugi strani:

In izraz desne je natančno naklon črte, za katero je ugotovljeno, da je povprečni razlog spremembe naklon sekanske črte na graf Y.

Znaki razloga za spremembe

Po dani definiciji je razlog za spremembe lahko pozitiven ali negativen, odvisno od tega, kako se vpletene magnitude razlikujejo, saj se te lahko povečajo ali zmanjšajo, glede na.

Če je razlog za spremembo pozitiven, to pomeni, da se spremeni in in v x So bili isti znak, to je, in povečan in x Tudi on. Ali toliko in kot x Zmanjšali so se.

Ko pa je razlog za spremembe negativen, to pomeni, da se je ena od velikosti povečala, druga.

Razlog za takojšnjo spremembo

Pogosto je veliko bolj zanimivo. V tem primeru je treba, da je variacija Δx izjemno majhna, nagiba na 0 (vendar brez 0, saj delitev med 0 ni definirana).

To se imenuje "prevzema mejo", v tem primeru pa se razmerje trenutnih sprememb imenuje "derivat" in s spoštovanjem do x in je označen kot dy/dx; Tako:

Razmerje ali trenutna hitrost sprememb je tudi enaka naklonu črte, v tem primeru pa je naklon tangentne črte do grafa in proti x.

Preprosti primeri

Rast osebe

Ker se rodijo, otroci rastejo s tempom, ki jih določa več dejavnikov, med katerimi izstopata genetika in hrana. Najvišje stopnje rasti se pojavijo v prvem letu življenja; Kasneje, v otroštvu in nato v puberteti, otroci običajno doživljajo "raztezanje", to je razlog za spremembo višine glede na čas in nato zmanjšajo.

Po puberteti fantje še naprej rastejo, vendar se stopnja zmanjša, dokler se ne prekličejo, ko dosežejo dokončno stališče odraslih.

Kava kul

Znano je dejstvo, da se kava ali vroča juha postopoma ohladi, ko ostane pri sobni temperaturi. Vendar se hitrost hlajenja upočasni bližje temperaturi kave ali juhe pri sobni temperaturi.

Eden od načinov za modeliranje tega pojava je skozi Newton hladilni zakon, V skladu s katero je hitrost prenašanja toplote sorazmerna z razliko med temperaturo snovi in ​​temperaturo okolice. Konstanta sorazmernosti k je značilna za snov:

T_tudi predstavlja temperaturo okolja.

Rešene vaje

Vaja 1

Izračunajte povprečno razmerje sprememb in s spoštovanjem do x, Glede na naslednje vrednosti:

in₁ = 3; in₂ = 10; x₁ = 2; x₂ = 5

Rešitev

V skladu s formulo:

Vrednosti, navedene v stavku, so zamenjane in operacija je rešena:

Vaja 2

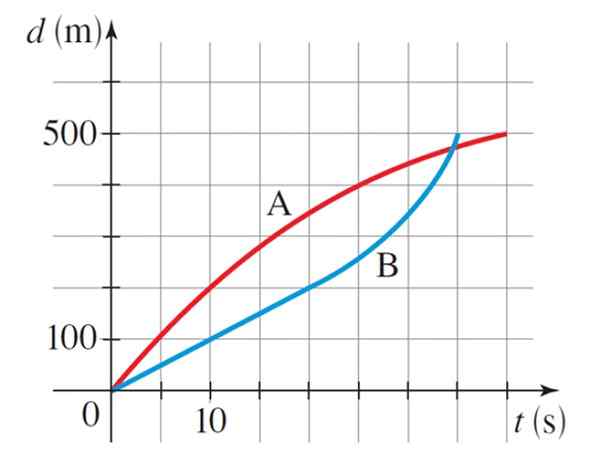
Graf prikazuje ustrezne krivulje razdalje v primerjavi s časom dveh olimpijskih drsalcev A in B v modalu 500 metrov. Kdo je zmagal na dirki? Kakšna je bila povprečna hitrost vsakega drsalca?

Rešitev

Ob opazovanju grafa je sledilo, da je drsalec B (Blue Curve) zmagal na dirki, saj je gostoval 500 m v 35 s, medtem ko je drsalec A (rdeča krivulja) to storila v 40 s.

Ustrezne povprečne hitrosti so bile:

Reference

1. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 1. Kinematika. Uredil Douglas Figueroa (USB).
2. Glencoe Science. Stopnja sprememb in naklona (2021). Okreval od: Glencoe.com.
3. Larson, r. (2012). Prekalenkulacija. 8. Izdaja. Cengage učenje.
4. Larson, r. (1986). Izračun z analitično geometrijo, 2. Izdaja. McGraw-Hill.
5. Stewart, J. (2011). Algebra na fakulteti, koncepti in konteksti. Brooks/Cole.