Kaj je linearna hitrost? (Z rešenimi vajami)

The Linearna hitrost Opredeljen je kot tisto, ki je vedno tangencialno za pot, ki ji sledi delček, ne glede na to. Če se delček vedno premika v pravokotni poti, ni problema, ki bi si predstavljal, kako vektor hitrosti spremlja to ravno črto.

Vendar se na splošno gibanje izvaja na krivulji poljubno. Vsak del krivulje je mogoče modelirati, kot da bi bil del radijskega kroga do, ki je na vsaki točki tangenta do poti.

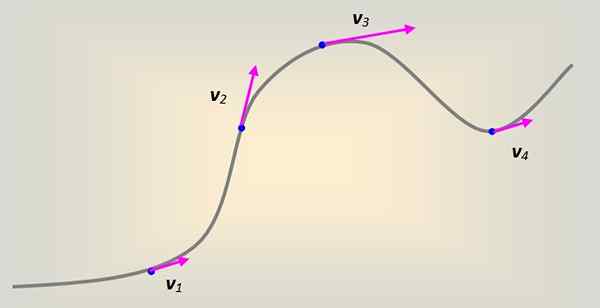
Slika 1. Linearna hitrost na mobilnem telefonu, ki opisuje krivorodno usmeritev. Vir: Self Made.

V tem primeru linearna hitrost spremlja tangencialno in ves čas na krivuljo na vsaki točki.

Matematično trenutna linearna hitrost je izpeljana položaja glede na čas. Biti r položaj vektorja delca v trenutku t, Potem je linearna hitrost podana z izrazom:

v = r'(T) = dr / dt

To pomeni, da linearna hitrost ali tangencialna hitrost, kot se imenuje, ni nič drugega kot sprememba položaja glede na čas.

[TOC]

Linearna hitrost v krožnem gibanju

Ko je gibanje na obodu, lahko gremo poleg delca na vsaki točki in vidimo, kaj se zgodi v dveh zelo posebnih smeri: ena od njih je tisti, ki vedno kaže na središče. To je naslov radialno.

Druga pomembna smer je tista, ki poteka na obodu, to je naslov tangencialna In linearna hitrost jo vedno ima.

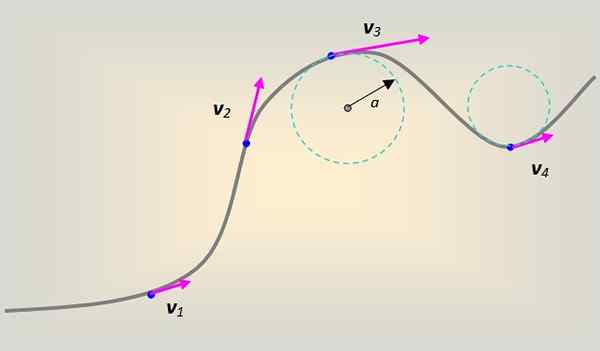
Lahko vam služi: Manometrični tlak: Pojasnilo, formule, enačbe, primeri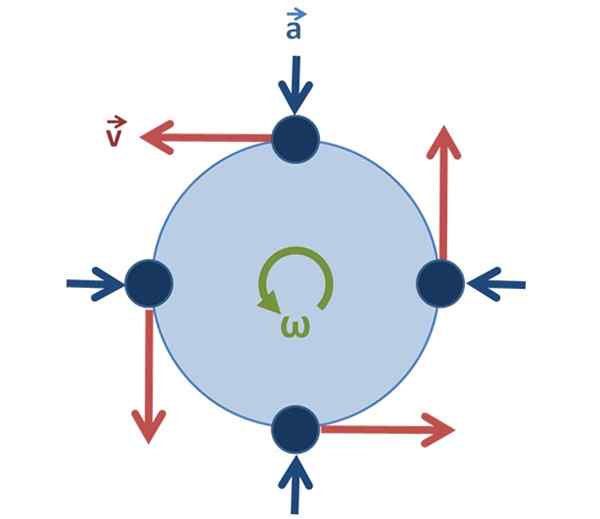Slika 2. Enotno krožno gibanje: Vektor hitrosti spreminja smer in smer, ko se delček vrti, vendar je njegova velikost enaka. Vir: Original by uporabnik: BREWS_OHARE, Svged od uporabnika: sjlegg [cc by-sa 3 3.0 (https: // creativeCommons.Org/licence/by-sa/3.0)].

V primeru enotnega krožnega gibanja je pomembno, da je ostalo nespremenjeno.

Za to gibanje je položaj kot funkcijo časa podan S (t), kje s Je on TOWD lok in t Čas je. V tem primeru je trenutna hitrost podana z izrazom V = ds/dt In je konstantno.

Če se tudi velikost hitrosti razlikuje (že vemo, da smer to vedno počne, sicer se mobilni telefon ne bi mogel obrniti), se soočamo.

Linearna hitrost, kotna hitrost in centripetalni pospešek

Gibanje delcev je mogoče videti tudi z vidika Pometen kot, Namesto da bi to storili iz potovanega cilja. V tem primeru govori o kotna hitrost. Za gibanje na radijskem krogu R, Obstaja razmerje med lokom (v radianih) in kot:

S = r θ

Izpeljava glede na obe strani:

ds/dt = r (dθ/dt)

Klicanje derivata θ glede na t kot kotna hitrost In če ga označite z grško črko ω "omega", imate to razmerje:

v = ωR

Centripetalni pospešek

Vsako krožno gibanje ima centripetalni pospešek, ki je vedno usmerjena proti središču oboda. Skrbi, da se hitrost spreminja, da se premika z delcem, ko se obrača.

Lahko vam služi: kalibracijska krivulja: za kaj je, kako to storiti, primeri

Centripetalni pospešek do_c tudi do_R Vedno kaže na središče (glej sliko 2) in je na ta način povezan z linearno hitrostjo:

do_c = v² /R

In z kotno hitrostjo kot:

do_c = (ΩR² /R = ω²R

Za enotno krožno gibanje položaj S (t) Je oblike:

S (t) = SO+ VT

Poleg tega mora imeti raznoliko krožno gibanje sestavni del pospeška Tangencialni pospešek do_T, ki obravnava spreminjanje obsega linearne hitrosti. Ja do_T  To je konstantno, Položaj je:

S (t) = s_tudi + v_tudiT + ½ a_Tt²

Z v_tudi Kot začetna hitrost.

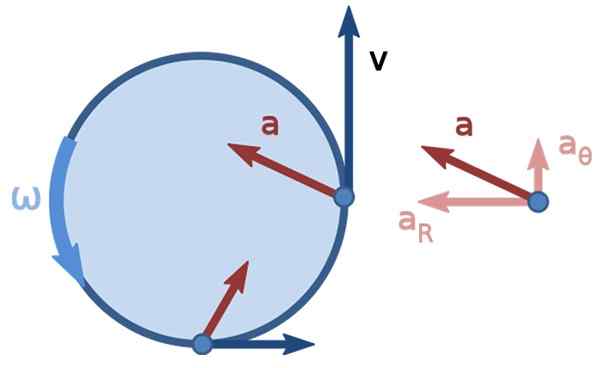Slika 3. Neenakomerno krožno gibanje. Vir: nonUniform_circular_motion.PNG: Brews Oharedorivative Work: Kooning Jons [CC BY-SA 3.0 (https: // creativeCommons.Org/licence/by-sa/3.0)].

Rešene vaje linearne hitrosti

Rešene vaje prispevajo k razjasnitvi pravilne uporabe konceptov in enačb.

-Vaja rešena 1 

Žuželka se premika na polmeru polkrog r = 2 m, začenši od počitka v točki, ob tem pa poveča linearno hitrost, s hitrostjo p m/s². Najti: a) Po tem, ko doseže točko B, b) Vektor linearne hitrosti v tistem trenutku, c) vektorski pospešek v tistem trenutku.

Slika 4. Žuželka se začne od A in doseže B na polkrožni poti. Ima linearno hitrost. Vir: Self Made.

Rešitev

a) Izjava kaže, da je tangencialni pospešek konstanten in je vreden π m/s², Potem je veljavno uporabiti enačbo za enakomerno raznoliko gibanje:

S (t) = s_tudi + v_tudiT + ½ a_T.t²

S s_tudi = 0 in V_tudi = 0:

S (t) = ½ a_T.t²

S = πR (Polovica dolžine oboda)

T = (2. πR /do_T) ^½ S = (2π.2 /π)^½S = 2 s

B v (t) = v_tudi + do_T. T = 2π gospa

Ko je v točki B, linearni vektor hitrosti kaže na navpično smeri navzdol v smeri (-in)::

Vam lahko služi: kakšna je dielektrična konstanta?

v (t) = 2π gospa(-in)

c) Tangencialni pospešek je že imel, centripetalni pospešek manjka, da bi imel hitrost vektor do:

do_c = v² / R = (2π)² / 2 m/ s² = 2π² gospa²

do = a_c (-x) + a_T (-in) = 2π²(-x)+ π (-in) gospa²

-Vaja Rešena 2

Delec se obrne v radijskem krogu 2.90 m. V določenem trenutku je njegov pospešek vreden 1.05 m/s² v smeri, ki tvori 32 s svojo smerno smerjo. Poiščite svojo linearno hitrost pri: a) ta trenutek, b) 2 sekundi kasneje, ob predpostavki, da je tangencialni pospešek konstanten.

Rešitev

a) Direktorat za gibanje je natančno tangencialni naslov:

do_T = 1.05 m/s² . cos 32 ° = 0.89 m/s² ; do_C = 1.05 m/s² . Sen 32 ° = 0.56 m/s²

Hitrost se razčisti do_c = v² / R kot:

v = (r.do_c)^1/2  = 1.27 m/s

b) Enačba za enakomerno raznoliko gibanje je veljavna na naslednji način: v = v_tudi + do_TT = 1.27 + 0.89 .2² m/s = 4.83 m/s

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill. 84-88.
2. Figueroa, d. Fizične serije za znanost in inženiring. Zvezek 3. Izdaja. Kinematika. 199-232.
3. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6^th… Ed Prentice Hall. 62-64.
4. Relativno gibanje. Obnovi se od: tečajev.Lumenarning.com
5. Wilson, J. 2011. Fizika 10. Pearson Education. 166-168.