Kaj je smernica? (Geometrija)

The direktiva V geometriji je sestavljen iz krivulje, površine ali volumna, ki ostane fiksirana, in določa način oblikovanja geometrijskega predmeta. Na primer, s črto so vzpostavljene druge krivulje, kot so stožčaste in revolucijske površine, kot je ravno krožni valj.

Krivulja smernice je lahko tudi obod. Ravni krožni valj lahko tvorimo tako, da zapustite polmer ri -r rión ri.

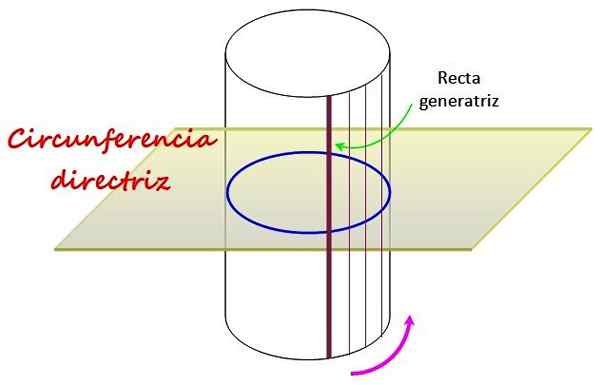
Slika 1. Ravni krožni valj ima kot vodnik krog, okoli katerega se premika ravna črta, imenovana Generatrix. Vir: f. Zapata.

Obseg, ki je na ravnini, narisani na sliki, določa obliko ukrivljene površine ravnega krožnega valja, ki nastane z vrtenjem črte okoli nje Ravni generatrik.

Če krivulja smernic ni obod, ampak druga krivulja, se ustvarijo druge vrste valja, na primer eliptični valj, katere smernica je elipsa.

Obseg lahko deluje tudi kot vodilo za ustvarjanje druge krivulje, takšen je primer Epitrokoid, Krivulja v ravnini, ki nastane s točko, ki je v manjši krog, ki se valja brez drsenja, okoli smernice.

Lažje ga je vizualno ceniti z naslednjo animacijo:

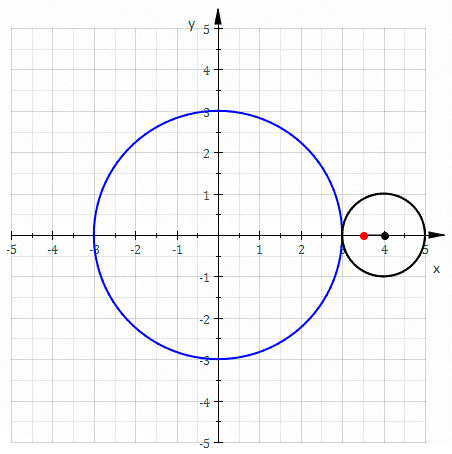Slika 2. Rdeča krivulja se imenuje Epitrocid in njegova krivulja smernic. Vir: Wikimedia Commons. Sam Derbyshire v angleški Wikipediji/cc by-s-s-s (http: // creativeCommons.Org/licence/by-sa/3.0/).

Krivulja smernic na valjastih površinah

Cilindrične površine so razvrščene po njihovi krivulji smernice v jeklenkah:

-Krožni

-Eliptična

-Parabolična

-Hiperbolična

Ko ima cilindrična površina smernico, ki leži v ravnini, pravokotni na linijo genetriksa, je enačba omenjene površine enaka smernici smernice.

Lahko vam služi: kakšen je odnos med območjem Rhombusa in pravokotnikom?

Jeklenke pripadajo skupini Kvadratne površine, katere enačba je drugi razred s tremi spremenljivkami. Splošni obrazec je:

Sekira² + Mimo² + Cz² + Dxy + exz + fyz + gx + hy + iz + k = 0

Kjer koeficienti a, b, c ... so resnične številke.

Jeklenke so najpogostejša in uporabna tridimenzionalna geometrijska telesa, ki jih je mogoče najti, zlasti ravne krožne jeklenke, druge vrste jeklenk, opisanih spodaj.

Ravni krožni valj

Njegova smernica je krog C, ki je v ravnini, pravokotni na valj, kot je prikazano na sliki 1, saj je črta genetriksa, ki poteka do C, da tvori stransko površino, pravokotna na C.

Enačba oboda c na ravnini XY, osredotočena na izvor (0,0), je:

x² + in² = R²

Kjer je R, bo polmer oboda očitno polmer valja. Višina H valja se razprostira vzdolž osi z, pravokotno na ravnino xy.

Eliptični valj

Smernica je elipsa v ravnini XY, osredotočena na izvor (0,0), katere enačba je:

Generatrix je črta, pravokotna na ravnino xy, ki se premika okoli elipse, da bi povzročila stransko površino. Elipsa je lahko na kateri koli višini z na ravnini xy.

Na primer, enačba elipse:

4x² + 9y² = 36

Krivulja smernice povzroči eliptični valj, katerega enačba je 4x² + 9y² = 36, plus z = 0. Če dodamo ta zadnji izraz, je jasno, da je površina.

Lahko vam služi: Napaka vzorčenja: formule in enačbe, izračun, primeri

Parabolični valj

V tem primeru je smernica prispodoba, ki je lahko v obliki y = x². Tako je valj usmerjen vzdolž osi z in tvori paribe z zlaganjem z vrhom v (0,0) vzdolž te osi.

Parabolični valj ima uporabo v sončni energiji, saj imajo nekateri kolektorji na ta način ogledala, skozi katero je v fokusu koncentrirana sončna svetloba. Ta točka preide ravno cev, znotraj katere olje doseže temperature do 400 ° C.

Hiperbolični valj

V hiperboličnem valju je enačba smernice hiperbola, osredotočena na izvor:

Valj je oblikovan v sklad.

Revolucijska površina

Krivulja smernice revolucijske površine je enaka osi revolucije, črta, okoli katere je krivulja, ki je odgovorna za ustvarjanje površine.

Krivulja, ki se vrti, ima lahko poljubno obliko, na ta način se ustvari območje, kot je razvidno iz te animacije:

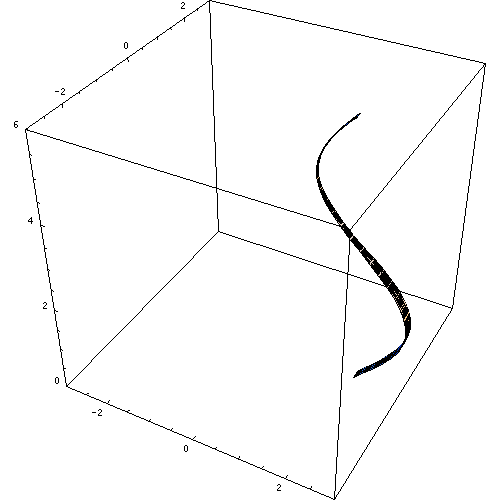Slika 3. Revolucijska površina. Vir: Wikimedia Commons. https: // nalaganje.Wikimedia.Org/wikipedia/commons/e/e7/rotatitatioerper_animation.Gif.

Če je okoli smernice obrnjena druga črta, dobimo že znani ravno krožni cilinder. Na enak način je mogoče dobiti druge revolucijske površine, kot so stožčasti, sferični in toroidni revolucijski površini.

Stožčasta površina

Konična površina nastane z gibanjem generacije generike, ki vedno poteka skozi fiksno ravno krivuljo ali krivuljo smernice, in s fiksno točko, imenovano Vertex, ki ne spada v smernico.

Vam lahko služi: matematično upanje: formula, lastnosti, primeri, vadba

Vertex ali konica razdeli stožec na dva dela, imenovana listi tudi veje.

Rešene vaje

- Vaja 1

Poiščite stransko območje visokega krožnega valja višine 25 cm, katere krivulja smernice je obseg polmera 6 cm, osredotočen na izvor.

Rešitev

Stransko območje jeklenke je produkt dolžine smernice po višini. Če je R polmer oboda in je H višina jeklenke, je območje podano z:

A = 2πr x h = 2πx 6 cm x 25 cm = 942.5 cm²

- Vaja 2

Imate naslednjo enačbo, ki ustreza kvadratni površini:

x² + in² + 2Z² +2xz - 2yz = 1

Navedite, kakšna površina je in kakšna je enačba smernice.

Rešitev

Dela z = k, kjer je k konstanten, dobimo:

x² + in² + 2K² +2kx - 2ky = 1

Izraza preuredimo na naslednji način:

(x² + 2kx) + (in²- 2ky) = 1-2k²

Kvadre morajo², Da ne bi spremenili nobenega od oklepajev:

(x² + 2kx + k² - k² ) + (in² - 2ky + k² - k²) = 1-2k²

(x² + 2kx + k²) - k²  + (in²- 2ky + k²) - k² = 1-2k²

Na ta način ostaja:

(x + k)² + (in - k)² = 1

Kot je enačba sredinskega kroga (-K, K) in polmera 1, je površina ravno krožni valj, tudi radio 1, dokler je črta genetriksa pravokotna na omenjeni obod.

Na primer, če naredimo k = 0, se enačba zmanjša na obod, osredotočen na izvor (0,0), katerega polmer je 1:

x² + in² = 1

Reference

1. Gaussians. Predstavljajo tri dimenzionalne površine. Okreval od: Gaussians.com.
2. Kindle, j. Teorija in problemi analitične geometrije. McGraw Hill. Serija Schaum.
3. Površine kot geometrijske kraje. Okrevano od: algebra.Frlp.UTN.Edu.ar.
4. Suárez, m. Površine. Pridobljeno od: Predmeti.Unq.Edu.ar.
5. Kvadratne površine. Okrevano od: sistemov.fciencias.Ne.mx.