Kakšen je modul za rezanje, togost ali striženje? (Rešene vaje)

On Rezani modul Opišite odgovor materiala na uporabo strižnega truda, ki ga deformira. Druge poimenovanja pogoste uporabe za rezalni modul so striženje, striženje, prečna elastičnost ali modul tangencialne elastičnosti.

Ko so prizadevanja majhna, so deformacije sorazmerne z njimi, po Hookejevem zakonu, rezalna konstanta pa je sorazmernost konstanta. Zato:

Rezani modul = rezanje/deformacijsko prizadevanje

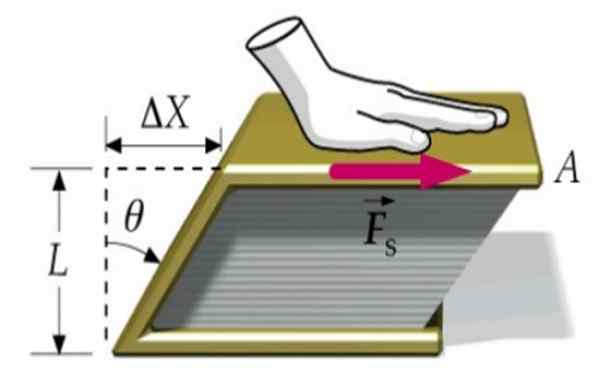
Slika 1. Knjiga je deformirana po zaslugi tangencialne sile FS. Vir: f. Zapata.

Recimo, da se na pokrov knjige uporablja sila, druga pa je pritrjena na površini tabele. Na ta način se knjiga kot celota ne premika, vendar se deformira, ko se zgornji pokrov premakne glede na spodnjo količino v količini Δx.

Knjiga sega od pravokotnega prečnega odseka do odseka v obliki paralelograma, kot vidimo na vrhunski sliki.

Biti:

τ = f/a

Trud ali rezanje napetosti, biti F velikost uporabljene sile in Do Območje, na katerem deluje.

Deformacija, ki jo povzroča, daje količnik:

Δ = Δx / l

Zato je rezalni modul, ki ga bomo označili za G,:

Na ta način je rezalni modul odgovoren za merjenje odpornosti notranjih ravnin predmeta, ki so vzporedni z uporabnim naporjem.

In ker Δx / l primanjkuje dimenzij, so enote G enake kot pri rezalnih prizadevanjih, kar je razlog med silo in območjem.

V mednarodnem sistemu enot so te enote Newton/Square Metro ali Pascal, skrajšano PA. In v anglo -saksonskih enotah je funt /kvadratni palec, skrajšano psi.

[TOC]

Vam lahko služi: enotno pravokotno gibanje: značilnosti, formule, vaje

Rezan modul za različne materiale

V skladu z delovanjem rezalnih sil, kot so opisane, predmeti ponujajo odpor, podoben tistemu v knjigi, v kateri notranje plasti drsijo. Ta vrsta deformacije se lahko pojavi le v trdnih telesih, ki imajo dovolj togosti, da se nasprotujejo deformiranju.

Po drugi strani tekočine ne ponujajo takšne odpornosti, vendar lahko doživijo volumske deformacije.

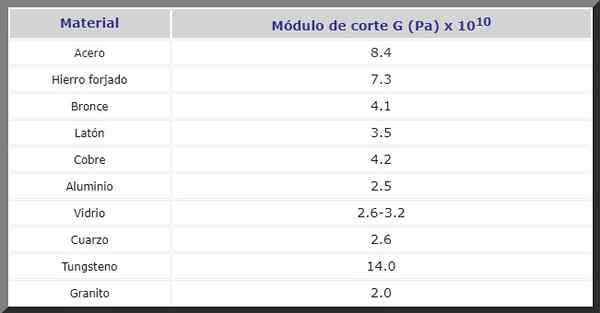
Slika 2. Vijaki v strukturah so podvrženi zmanjšanju prizadevanj. Vir: Pixnio.

Nato imate G -CUT modul v P za različne materiale, ki se pogosto uporabljajo v gradnji in pri izdelavi strojev in rezervnih delov vseh vrst:

Eksperimentalna mera rezalnega modula

Če želite najti vrednost rezalnega modula, morate preizkusiti vzorce vsakega materiala in preučiti svoj odziv na uporabo rezalnega napora.

Vzorec je palica, narejena z materialom, z radiem R in dolžina L znano, ki je pritrjena na enem koncu, druga.

Jermenica ima vrv, na čigar prosti konec je obešena tehta, ki izvaja silo F Na palici skozi vrv. In ta sila posledično ustvari trenutek M V palici, ki nato obrne majhen kot θ.

Shema montaže je razvidna na naslednji sliki:

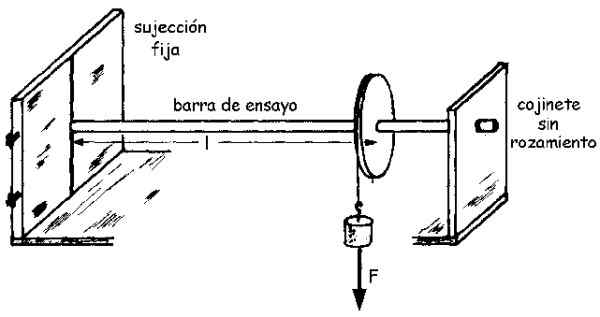Slika 3.- Eksperimentalni sklop za določitev strižnega modula ali razrezanja tanke preskusne palice. Vir: Univerza v Valladolidu.

Velikost trenutka M, ki jih označujemo kot M (brez krepkega) je povezan z zasukanim kotom θ skozi rezani modul G v skladu z naslednjo enačbo (ugotovi ga preprost integral):

Ker je velikost trenutka enaka produlutu modula sile F s polmerom škripca R_str:

Lahko vam služi: Torricelli Experiment: Atmosferski tlačni ukrepi, pomen

M = f.R_str

In sila je teža, ki visi W, tako:

M = w.R_str

Nadomeščanje v enačbi magnitude trenutka:

Imate razmerje med težo in kotom:

Kako najti g?

To razmerje med spremenljivkami W in θ Je linearna, zato se merijo različni koti, ki visijo različne teže.

Pari teže in kota so grafi na milimetrskem papirju, najboljša črta, ki poteka skozi eksperimentalne točke, se prilagodi in nagib se izračuna m omenjene črte.

 Od tam sledi, da:

Vaje z raztopino

- Vaja 1

2 palica.5 metrov dolg in radio 4.5 mm je pritrjeno na enem koncu. Drugi se poveže s 75 cm radijskim jermenijem, ki ima 1 1 težo.3 kg. Obrnjeni kot je 9.5.

S temi podatki se zahteva, da izračunamo rezani modul G palice.

Rešitev

Iz enačbe:

GASS G:

In vrednosti, navedene v izjavi, so zamenjane, pri čemer pazljivo izražajo vse podatke v mednarodnem sistemu enot, če:

R = 4.5 mm = 4.5 x 10 ^-3 m

R_str = 75 cm = 0.075

Premik iz kilogramov (dejansko so kilogrami - sila) na Newton pomnoži do 9.8:

W = 1.3 kg-sila = 1.3 x 9.8 n = 12.74 n

In končno, stopinje morajo biti na radianih:

9.5. = 9.5 x2π /360 radianov = 0.1658 Radianes.

Z vsem tem imate:

= 2.237 x 10¹⁰ Pa

- Vaja 2

Gel kocka je 30 cm. Eden od njegovih obrazov je določen, hkrati pa se na nasprotni obraz uporabi vzporedna sila 1 n.

Lahko vam služi: magnetizacija: orbitalni in vrteni magnetni trenutek, primeri

Zahteva se s temi podatki:

a) Obseg strižne napetosti

b) enotna deformacija δ

c) Vrednost rezalnega modula

Rešitev

Obseg strižnega stresa je:

τ = f/a

Z:

A = stran² = (30 x 10^-2 cm)² = 0.09 m²

Zato:

τ = 1 n / 0.09 m² = 11.1 Pa

Rešitev b

Enotna deformacija ni nič drugega kot vrednost δ, ki jo daje:

Δ = Δx / l

Premik obraza, ki je podvržen sili, je 1 cm, potem pa:

Δ = 1/30 = 0.0333

Rešitev c

Modul za rezanje in količnik med rezalnim naporom in deformacijo enote:

G = trud rezanja/deformacije

Zato:

G = 11.1 Pa /0.033 = 336.4 pa

Reference

1. Pivo, f. 2010. Mehanika materialov. McGraw Hill. 5. Izdaja.
2. Franco Garcia,. Togo trdno. Slišite merjenje modula. Pridobljeno iz: sc.Ehu.je.
3. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6. Ed Prentice Hall.
4. Resnick, r. (1999). Fizično. Vol. 1. 3. izd. v španščini. Continental uredništvo s.Do. od c.V.
5. Univerza v Valladolidu. Oddelek za fiziko kondenzirane snovi. Izbira težav. Okreval od: www4.grozdje.je.