Kakšno je ravnovesje delca? (S primeri)

On ravnovesje delcev To je stanje, v katerem je delček, ko se zunanje sile, ki delujejo nanje. To pomeni, da ohranja stalno stanje, tako da se lahko zgodi na dva različna načina, odvisno od določene situacije.

Prvi je v statičnem ravnovesju, v katerem je delček negiben; In drugo je dinamično ravnovesje, kjer se vsota sil odpove, vendar ima delček enakomerno pravokotno gibanje.

Slika 1. Ravnotežja kamnine. Vir: Pixabay.

Model delcev je zelo uporaben pristop k preučevanju gibanja telesa. Sestavljen je iz predpostavke, da je celotna masa telesa koncentrirana v eni točki, ne glede na velikost predmeta. Na ta način lahko zastopate planet, avto, elektron ali biljardno žogo.

[TOC]

Nastala sila

Na točki, ki predstavlja predmet, so sile, ki vplivajo nanj. Vse te sile lahko nadomestimo z enim, ki ima enak učinek, ki se imenuje posledična sila tudi Neto sila In označena je kot F_R ali f_N.

Po Newtonovem drugem zakonu, ko je neuravnotežena posledična sila, telo doživi pospešek, sorazmerno s silo:

F_R = m.do

Kje do Objekt pridobi pospešek zaradi dejanja sile in m To je masa predmeta. Kaj se zgodi, če se telo ne pospeši? Natančno tisto, kar je bilo navedeno na začetku: telo je v mirovanju ali se premika z enakomernim pravokotnim gibanjem, ki nima pospeška.

Za delček v ravnovesju je veljavno zagotoviti:

F_R = 0

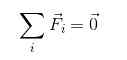
Ker dodajanje vektorjev ne pomeni nujno modulov, se morajo vektorji razgraditi. Tako je veljavno izraziti:

F_x = m.do_x = 0; F_in = m.do_in = 0; F_z = m.do_z = 0

Brezplačni diagrami telesa

Za vizualizacijo sil, ki delujejo na delcu, je treba narediti prosti karoserijski diagram, v katerem so vse sile, ki delujejo na predmet.

Vam lahko služi: Zemljina magnetosfera: značilnosti, struktura, plini

Prejšnje enačbe so vektorska narava. Z razpadom sil jih odlikuje znaki. Na ta način je mogoče, da je vsota njegovih komponent nič.

Sledijo pomembni pokazatelji, da je risba koristna:

- Izberite referenčni sistem, v katerem se nahaja največje število sil na koordinatnih osi.

- Teža je vedno navpično navzdol.

- V primeru obstoja dve ali več površin v stiku obstajajo normalne sile, ki jih vedno vlečejo s potiskanjem telesa in pravokotno na površino, ki ga izvaja.

- Za delček v ravnotežju je lahko trenje vzporedno s kontaktno površino in nasprotuje morebitnemu gibanju, če se delček upošteva v mirovanju ali vsekakor v nasprotju, če se delček premika z MRU (enotno pravokotno gibanje).

- Če je vrv, se napetost vedno vleče po njej in vleče telo.

Načini uporabe stanja ravnotežja

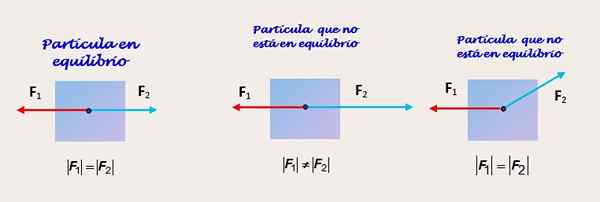Slika 2. Dve uporabljeni sili na različne načine na istem telesu. Vir: Self Made.

Dve sili enake velikosti in smeri ter nasprotnih čutov

Slika 2 prikazuje delček, na katerem delujeta dve sili. Na sliki na levi delček prejme delovanje dveh sil F₁ in f₂ ki imajo enako velikost in delujejo v isti smeri in v nasprotnih čutilih.

Delec je v ravnovesju, vendar kljub temu z informacijami, če pod pogojem, da ni mogoče vedeti, ali je ravnovesje statično ali dinamično. Potrebnih je več informacij o inercialnem referenčnem sistemu.

Dve sili različnih velikosti, enakih smeri in nasprotnih čutov

Sredinska slika prikazuje isti delček, ki tokrat ni v ravnovesju, saj velikost sile F₂ je večji kot pri F₁. Zato obstaja neuravnotežena sila in predmet ima pospeševanje v isti smeri kot F₂.

Vam lahko služi: Darcy Law

Dve sili enake velikosti in drugačne smeri

Končno na sliki na desni opazimo telo, ki ni v ravnovesju. Čeprav f₁ in f₂ Imajo enako velikost, silo f₂ Ni v isti smeri kot 1. Navpična komponenta F₂ Ne preprečuje nobenega drugega in delce doživlja pospeševanje v tej smeri.

Tri sile z drugačno smerjo

Ali je delček, predložen trem silam, v ravnovesju? Da, dokler pri postavljanju konice vsakega, je nastala figura trikotnik. V tem primeru je vektorska vsota nična.

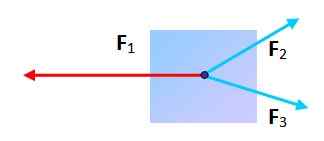Slika 3. Delček, ki je podvržen delovanju 3 sil, je lahko v ravnovesju. Vir: Self Made.

Trenje

Sila, ki pogosto posega v ravnovesje delca, je statično trenje. Je posledica interakcije predmeta, ki ga predstavlja delček s površino drugega. Na primer, knjiga v statičnem ravnovesju na nagnjeni tabeli je modelirana kot delček in ima prosti karoserijski diagram, kot je naslednje:

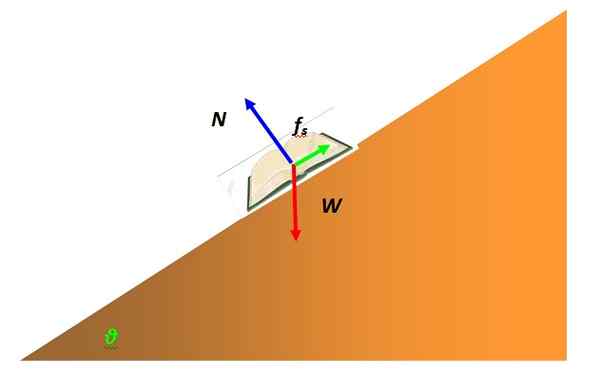Slika 4. Brezplačni karoserijski diagram knjige na nagnjeni ravnini. Vir: Self Made.

Sila, ki preprečuje, da bi knjiga zdrsnila skozi površino nagnjene ravnine in ostane v mirovanju, je statično trenje. Odvisno je od narave površin v stiku, ki mikroskopsko imajo hrapavost z vrhovi, ki so zaklenjeni, kar ovira gibanje.

Najvišja vrednost statičnega trenja je sorazmerna z normalno silo, ki površino izvaja na podprtem predmetu, vendar pravokotna na omenjeno površino. V primeru knjige je označeno v modri barvi. Matematično je izraženo na naslednji način:

F_več∝ N

Konstanta sorazmernosti je Statični koeficient trenja μ_s, ki je določena eksperimentalno, je brezdimenzionalna in je odvisna od narave površin v stiku.

F_{S max} = μ_s N

Dinamično trenje

Če je delček v dinamičnem ravnovesju, se gibanje že zgodi in statično trenje ne posreduje več. Če je prisotna kakšna sila trenja, ki nasprotuje gibanju, deluje dinamično trenje, katere velikost je stalna in daje:

Vam lahko služi: kakšne so toplotne lastnosti in kaj so? (S primeri)

F_k = μ_k N

Kje μ_k Je on Dinamični koeficient trenja, ki je odvisno tudi od vrste površin v stiku. Tako kot statični koeficient trenja je tudi brezdimenzionalna in njegova vrednost je eksperimentalno določena.

Vrednost koeficienta dinamičnega trenja je običajno manjša od vrednosti statičnega drgnjenja.

Rešen primer

Knjiga na sliki 3 je v mirovanju in ima maso 1.30 kg. Letala ima naklon kot 30 °. Poiščite koeficient statičnega trenja med knjigo in površino ravnine.

Rešitev

Pomembno je izbrati ustrezen referenčni sistem, glejte naslednjo sliko:

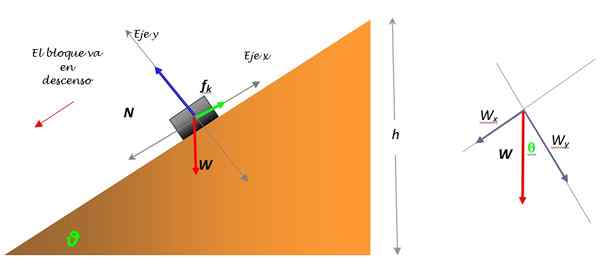Slika 5. Knjiga -Diagram telesa brez nagnjene ravnine in razgradnjo teže. Vir: Self Made.

Teža knjige ima velikost W = mg, Vendar ga je treba razbiti na dve komponenti: W_x in W_in, Ker je edina sila, ki ne pade tik nad katero koli koordinatno osi. Razpad teže opazimo na sliki na levi strani.

W_in = mg.cosθ = 1.30 x 9.8 x cos 30º n = 11.03 n

W_x = mg.Senθ = 1.30 x 9.8 x Sen 30 ° = 6.37 n

2. mesto. Newtonov zakon za navpično osi je:

N - wy = 0

N = mg. cos θ = 11.03 n.

Uporaba 2. Newtonov zakon za osi X, ki se odloči za pozitivno smer možnega gibanja:

W_x - F_s = 0

Največje trenje je F_{s Max}= μ_sN, Zato:

W_x - μ_sN = 0

μ_s = W_x / N = 6.37/11.03 = 0.58

Reference

1. Rex, a. 2011. Osnove fizike. Pearson. 76 - 90.
2. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 1. 7^ma. Ed. Cengage učenje. 120 - 124.
3. Serway, r., Vulle, c. 2011. Osnove fizike. 9^na Ed. Cengage učenje. 99-112.
4. Tippens, str. 2011. Fizika: pojmi in aplikacije. 7. izdaja. MacGraw Hill. 71 - 87.
5. Walker, J. 2010. Fizika. Addison Wesley. 148-164.