Značilnosti kartografske konične projekcije, prednosti, slabosti

The Kartografska stožčasta projekcija Zanj je značilno projiciranje točk sferične površine na površini stožca, katerega vrhova se nahaja na osi, ki poteka skozi drogove in je tangentna ali se suši na kroglo. Stožec je površina, ki jo je mogoče odpreti v ravnini, ki tvori kotni sektor in ne da bi deformirali projicirane črte na njem.

Matematik Johann Heinrich Lambert (1728 - 1777) je bil tisti, ki je zasnoval to projekcijo in se prvič pojavil v svoji knjigi Perspektiva Freye (1759), kjer je zbral več teorij in razmišljanj o napovedih.  

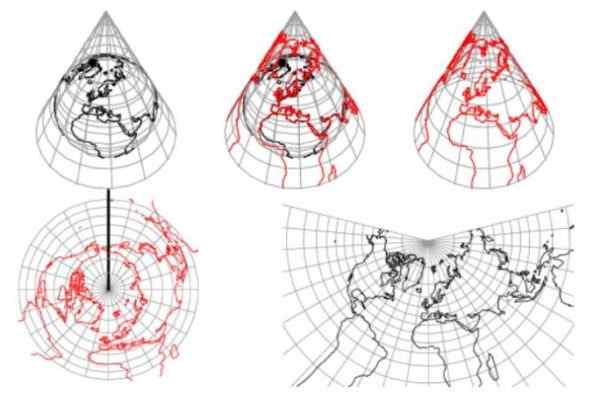
Slika 1. Stožčasta projekcija. Vir: Weisstein, Eric W. "Konična projekcija.”Iz spletnega vira MathWorld-A Wolfram.

V stožčastih projekcijah zemeljske površine postanejo radialne črte, osredotočene na tono, z enakim kotnim razmikom in zemeljskimi vzporednicami postanejo koncentrični krožni loki do vrha.

Slika 1 kaže, da stožčasta projekcija ne omogoča, da sta obe polobli predstavljeni. Poleg tega je jasno ugotovljeno, da se razdalje popačejo od vzporednic, ki prestrežejo stožec. 

Zaradi teh razlogov se ta vrsta projekcije uporablja za predstavljanje regij srednje širine, obsežne od vzhoda do zahoda in manjšega sever-jug. Takšen je primer celinske regije Združenih držav Amerike.

[TOC]

Prednosti

Zemlja lahko približa radijsko sfero 6378 km, če upoštevamo, da so vse kopenske in vodne mase na tej veliki sferi. Gre za pretvorbo te površine, ki objekt zajema v tri dimenzije, kot je krogla, v drugem predmetu v dveh dimenzijah: ravni zemljevid. To prinaša neprijetnosti, ki jih je ukrivljena površina izkrivljala, in jo želi projicirati na ravnino.

Vam lahko služi: reka júcar

Kartografske projekcije, kot je stožčasta projekcija, poskušajo to težavo rešiti z nižjo možno izgubo natančnosti. Zato obstaja več možnosti za izdelavo projekcije, glede na značilnosti, ki so poudarjene.

Med temi pomembnimi značilnostmi so razdalje, površina, koti in drugo. Najboljši način, da jih vse obdržite, je zastopanje zemlje v 3D v obsegu. Ampak to ni vedno praktično.

Prevoz sveta povsod ni enostavno, saj zaseda glasnost. Prav tako ni mogoče videti celotne površine zemlje hkrati in ni mogoče reproducirati vseh podrobnosti v modelu obsega.

Lahko si predstavljamo, da je planet pomaranča, olupite oranžno in razmažite lupino na mizo ter poskušate obnoviti podobo oranžne površine. Jasno je, da se bo v postopku izgubilo veliko informacij.

Možnosti projekcije so naslednje:

- Projekt na letalu oz

- Na valju, ki ga je mogoče razviti kot pravokotna ravnina.

- Končno o stožcu.

Sistem stožčaste projekcije ima prednost, ki je natančna za vzporednice, izbrane za prestrezanje projekcijskega stožca.

Poleg tega ohranja praktično nedotaknjeno orientacijo po celotnih meridianih, čeprav lahko po njih nekoliko izkrivlja lestvico za širine, ki so oddaljene od standardnih ali referenčnih vzporednic. Zato je primerno predstavljati zelo obsežne države ali celine.

Enako oddaljena stožčasta projekcija

To je sistem stožčaste projekcije, ki ga je prvotno uporabljal Ptolemej, grški geograf, ki je živel med 100 in 170 d leti. C. Kasneje leta 1745 je bil izboljšan.

Lahko vam služi: Western Cordillera de Columbia

Pogosto se uporablja v atlasu regij z vmesnimi širinami. Primerno je pokazati območja z nekaj stopinjah širine, ki spadajo v eno od ekvatorialnih polomec.

V tej projekciji so razdalje resnične po celotnih meridianih in v obeh standardnih vzporednicah, to je vzporednic, izbranih za prestrezanje s projekcijskim stožcem. 

V enakodajni stožčasti projekciji se točka na krogli radialno razteza, dokler se preseči s tangentnim ali sekanskim stožcem, ki kot projekcijsko središče je v središču krogle.

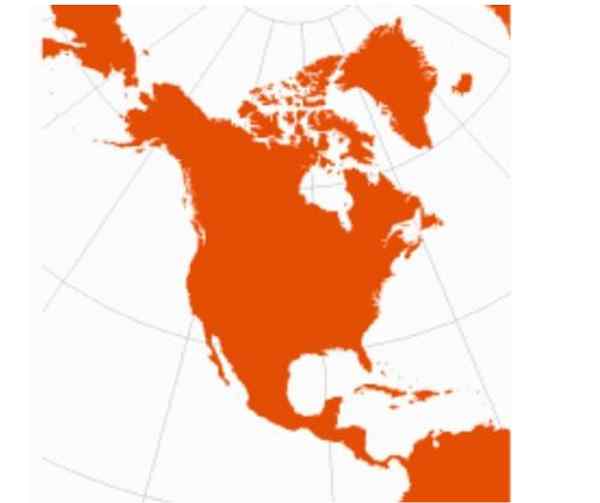Slika 2. Severna Amerika z enako oddaljeno stožčasto projekcijo. Vir: radikalna kartografija.

Slabosti

Glavna pomanjkljivost stožčaste projekcije je, da ni uporabna za ekvatorialna regija.

Poleg tega stožčasta projekcija ni primerna za preslikavo velikih regij, temveč posebna področja, kot je Severna Amerika.

Albertova stožčasta projekcija

Uporabite dve standardni vzporednici in ohranite območje, čeprav ne lestvica in oblika. To vrsto stožčaste projekcije je predstavil H. C. Albers leta 1805.

Vsa področja na zemljevidu so sorazmerna z ustreznimi na Zemlji. V omejenih regijah so naslovi razmeroma natančni. Razdalje ustrezajo tistim iz sferične površine na standardni vzporednici.

V ZDA se uporablja ta projekcijski sistem za zemljevide, ki prikazujejo meje držav zveze, za katere so izbrane kot standardne vzporednice na 29,5 ° N in 45,5 ° N, kar ima za posledico največjo napako lestvice 1, 25%.

Zemljevidi, narejeni s to projekcijo.

Vam lahko služi: petrologija

Konična projekcija po Lambertu

Leta 1772 ga je predlagal istoimenski matematik in švicarski geograf. Njegova glavna značilnost je, da uporablja tangentni ali sekanski stožec za sfero in projekcija ohranja kote invariantne. Te lastnosti so zelo koristne pri navigacijskih letalskih črkah. 

Geološka služba ZDA (USGS) uporablja Lambertovo stožčasto projekcijo. V tej projekciji so razdalje resnične v celotnih standardnih vzporednicah.

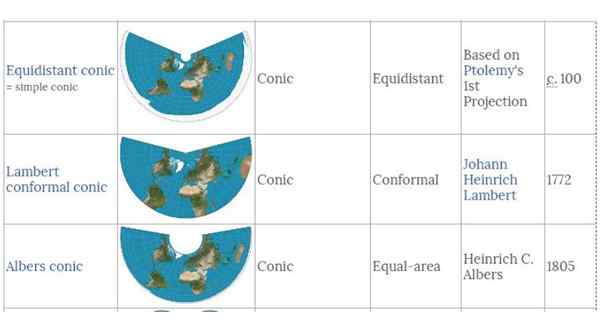Slika 3. Različne stožčaste projekcije severne poloble na desni strani, datum ustvarjanja. Vir: Wikimedia Commons.

V stožčasti projekciji Lamberta naslove ostajajo razumno natančni. Območja in oblike so malo izkrivljeni v položajih, ki so blizu standardnih vzporednic, vendar se sprememba oblike in površine poveča z ločitvijo nanje. 

Ker je cilj te projekcije vzdrževati navodila in kote, ki so enaki izvirnikom na sferi ali elipsoidu.

Namesto tega gre za metodo analitične projekcije, ki temelji na matematičnih formulah.

Osnovne zemljevide USGS za 48 celinskih izjav uporabljajo kot standardne 33 ° in 45 ° N vzporednic, kar je največjo napako v 2,5% zemljevidov.

Za navigacijske kartice na Aljaski so uporabljene osnovne vzporednice 55 ° N in 65 ° N. Po drugi strani pa Nacionalni atlas Kanade USA 49 ° N in 77 ° N.

Reference

1. Geohunter. Lambert konformni konični projekt. Okreval od: geo.Lovec.CUNY.Edu
2. GISGOGRAFIJA. Konična projekcija: Lambert, Albers in Pologyconic. Okrevano od: gisgeografija.com
3. GISGOGRAFIJA. Kaj so projekcije zemljevidov? Okrevano od: gisgeografija.com
4. USGS. Zemljevidne projekcije. Okreval od: ICSM.Gov.Au
5. Weisstein, Eric W. „Albers Equaet-Aea Conic Project.”Ozdravljeno od: Mathworld.Wolfram.com
6. Weisstein, Eric W. "Konična projekcija" je bila obnovljena od: Mathworld.Wolfram.com
7. Weisstein, Eric W. "Lambert Forformal Conic Project" se je okreval od: Mathworld.Wolfram.com
8. Wikipedija. Seznam projekcij zemljevidov. Pridobljeno iz: v.Wikipedija.com