Posebne in univerzalne značilnosti predlogov

The posebne in univerzalne predloge So glavna razvrstitev kategorij predloge. Predlagal jih je Aristotel in so del preučevanja logike.

Aristotelijska logika opredeljuje predlog kot molitev, ki nekaj potrjuje ali zanika. To je argumentirano in absolutno. Kategorični predlogi so tisti, v katerih je potrjena ali zanika, da je del (ali skupno) nekaj. Odvisno od njihovih lastnosti so univerzalne ali posebne.

Primer določene predloge bi bil "nekatere države imajo obalo", medtem ko bi bil univerzalni predlog "živa bitja smrtna". 

Aristotelovske predloge

To je bil Aristotel (384.C. - 322 a.C.), ki je predlagal kategorične predloge kot celoto. Ustanovljeni so bili kot začetni del strukture logike govorjenega jezika.

Teorija predloga pojasnjuje, da je njegov cilj opozoriti, ali je predikat del predmeta ali ne.

Univerzalne predloge

Univerzali so tisti, ki se nanašajo na celotno skupino subjekta. O določenem elementu ni govora, ampak od vsega.

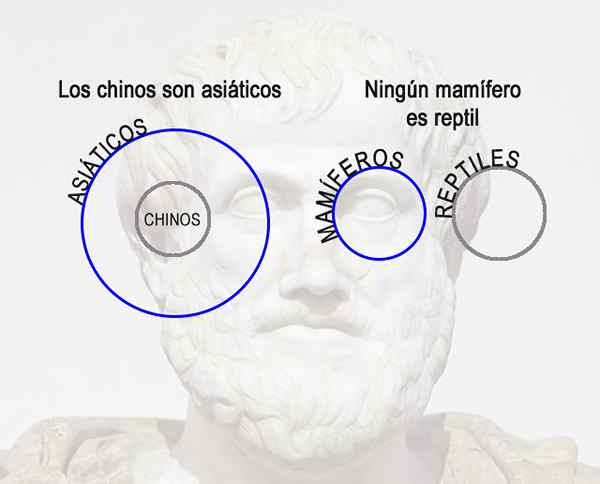
Na primer, molitev "All Dogs Ladran" je univerzalni predlog. Daje isto lastnost (laje) vse člane te skupine (psi).

"Človeški sesalci" je tudi še en primer univerzalnega predloga. Predmet je "ljudje" in predikat je "oni so sesalci".

Posebne predloge

Posebne predloge, za razliko od zgoraj, se nanašajo na določen del skupine.

Predlog "nekatere ptice letijo", je poseben, saj se nanaša na nekatere elemente celotne skupine.

Enako velja za molitev "Nekateri ljudje so blond". V tem primeru "nekateri ljudje" predstavljajo temo in "so blond" je predikat.

4 glavne oblike predloge

Ne glede na to, ali so univerzalni ali posamezniki, so lahko vse predloge pritrdilne ali negativne.

Pritrdilno. Pritrdilni so tisti, ki potrjujejo navedeno izjavo. To pomeni, da pozitivno podpirajo predikat molitve. Primer pritrdilne univerzalne predloge je "vse Maullanske mačke". To pozitivno navaja, da celotna skupina predmeta izvaja predikatno dejanje.

Pritrdilna trditev je "nekatere mačke so bele". To ni vključeno v celotno skupino znotraj predikata, ampak le nekaj elementov tega.

Negativno. Medtem negativne predloge zanikajo resničnost izjave. Molitev "Nobena ptica nima slive" je negativna univerzalna predlog. To potrjuje zanikanje predikata v celotni skupini, na katero se nanaša.

Medtem ko je stavek s strukturo "nekaterih ptic ne letijo". To zanika pripadnost dela skupine predikatu.

Na podlagi tega je Aristotel ugotovil, da obstajajo 4 možni načini kategorične predloge. Tako je ustvaril klasifikacijo, da bi jih podrobno preučil.

Oblika A: pritrdilne univerzalne predloge

Vsak subjekt je pridigan. Na primer: vsi planeti so okrogli.

Obrazec E: negativni univerzalni predlogi

Nobena tema ni pridigana. Na primer: noben planet ni ravna.

Obrazec I: Pritrdilne posebne predloge

Nekateri subjekt je pridigan. Na primer: Nekatera vrata so narejena iz lesa.

Obrazec ali: posebne negativne predloge

Nekateri subjekt ni pridigan. Na primer: Nekatera vrata niso kovinska.

Vaje

Ugotovite, katera od štirih možnih oblik kategoričnih predlogov pripada naslednjim argumentom.

- "Vsi Evropejci so ljudje"

[toggy_button title = "odgovor"] je pritrdilen univerzalni predlog, saj je tema, kot je vse pridigana.[/toggy_button]

- "Noben sesalec ni nesmrten"

[toggy_button title = "odgovor"] je negativen univerzalni predlog, saj subjekt kot vse ni pridigano.[/toggy_button] 

- "Nekateri avtomobili so električni"

[toggy_button title = "odgovor"] je pritrdilen predlog, saj je tema pridigana.[/toggy_button]

- "Nekateri avtomobili niso pet vrat"

[toggy_button title = "odgovor"] je poseben negativni predlog, saj subjekt ne pridiga.[/toggy_button]

Reference

1. Kategorični predlogi. (2011) Filozofipi.com
2. Razvrstitev spropozicij. (2013) Izrazitski Sveto pismo1.Datoteke.WordPress.com
3. Predhodna predloga. Matematexx.Datoteke.WordPress.com
4. Filozofija 103: Uvod v logične Vennove diagrame standardnih oblik kategoričnih predlogov. (2004) Filozofija.Zemljišče.Edu
5. Kategorični predlogi. (2017) Britannica.com
6. Kategorični predlogi. (2017) Newworldiklopedija.org