Vsota asociativne lastnine, množenje, primeri, vaje

The asociativna lastnina vsote predstavlja asociativno naravo operacije dodaja v različne matematične sklope. Povezuje tri (ali več) elemente teh sklopov, imenovanih A, B in C, tako da je vedno izpolnjen:

a + (b + c) = (a + b) + c

Na ta način je zagotovljeno, da je rezultat, ne glede na to, kako združiti operacijo.

Slika 1. Pri aritmetičnih in algebrskih operacijah večkrat uporabljamo asociativno lastnost vsote. (Risba: Freepik Sestava: F. Zapata)

Vendar je treba opozoriti, da asociativna lastnina ni sinonim za komutativno lastnino. Se pravi, vemo, da vrstni red dodatkov ne spremeni vsote ali da vrstni red dejavnikov ne spremeni izdelka. Torej za vsoto lahko pišete takole: a + b = b + a.

Vendar je v asociativni lastnosti drugače, saj se ohrani vrstni red elementov in spremembe je operacija, ki se najprej izvaja. Kar pomeni, da to najprej ni pomembno (B+C) in k temu rezultatu dodajte, da začnete dodajati B in k rezultatu dodajte c.

Številne pomembne operacije, kot je vsota, so asociativne, vendar ne vse. Na primer v odštevanju resničnih številk se zgodi:

A - (b - c) ≠ (a - b) - c

DA A = 2, B = 3, C = 1, potem:

2- (3 - 1) ≠ (2 - 3) - 1

0 ≠ -2

[TOC]

Asociativna lastnost množenja

Kot je bilo storjeno za vsoto, asociativna lastnost množenja kaže, da:

a ˟ (b ˟ c) = (a ˟ b) ˟ c

Vam lahko služi: vsota polinomov, kot je to, primeri, vaje

V primeru nabora resničnih števil je enostavno preveriti, ali je vedno. Na primer, z uporabo vrednosti a = 2, b = 3, c = 1, morate:

2 _˟ (3 _˟ 1) = (2 _˟  3) _˟ 1 → 2 _˟ 3 = 6 _˟ 1

6 = 6

Realne številke ustrezajo asociativni lastnost vsote in množenja. Po drugi strani je v drugem nizu, kot je vektorji, vsota asociativna, vendar navzkrižni ali vektorski izdelek ni.

Uporaba asociativne lastnosti množenja

Prednost, ki jo je treba izpolnjevati operacije, v katerih je srednja asociativna lastnina, je izpolnjena. To močno olajša resolucijo.

Recimo na primer, da so v majhni knjižnici 3 police s po 5 zabavami. V vsaki zabavi je 8 knjig. Koliko knjig je skupaj?

Operacijo lahko izvajamo na naslednji način: Skupne knjige = (3 x 5) x 8 = 15 x 8 = 120 knjig.

Ali tako: 3 x (5 x 8) = 3 x 40 = 120 knjig.

Slika 2. Uporaba asociativne lastnosti množenja je izračun števila knjig na vsaki polici. Slika, ki jo je ustvaril F. Zapata.

Primeri

-V sklopih naravne, celotne, racionalne, resnične in zapletene številke je izpolnjena asociativna lastnost vsote in množenja.

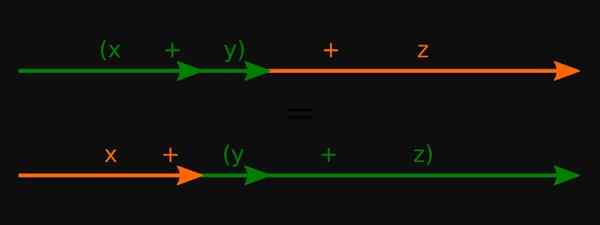Slika 3. Za realne številke je izpolnjena asociativna lastnost vsote. Vir: Wikimedia Commons.

-Za polinome se uporabljajo tudi pri teh operacijah.

-V primerih odštevanja, delitve in eksponentacije se asociativna lastnina ne izpolnjuje v realnem številu ali polinomih.

Vam lahko služi: Orthoedro: formule, območje, prostornina, diagonala, primeri

-V primeru matric je asociativna lastnost izpolnjena za vsoto in množenje, čeprav v slednjem primeru ni mogoče izpolniti. To pomeni, da je glede na matrike A, B in C res, da:

(A x b) x c = a x (b x c)

Ampak ... a x b ≠ b x a

Asociativna lastnina v vektorjih

Vektorji tvorijo drugačen niz kot resnične številke ali zapletene številke. Operacije, opredeljene za nabor vektorjev, so nekoliko drugačne: obstajajo vsota, odštevanje in tri vrste izdelkov.

Vsota vektorjev izpolnjuje asociativno lastnost, pa tudi številke, polinome in matrike. Kar zadeva skalarne izdelke, plezanje po vektorju in križu, ki so narejeni med vektorji, se slednji ne srečuje, toda skalarni izdelek, ki je še ena vrsta delovanja med vektorji, ga izpolnjuje ob upoštevanju naslednjega:

-Produkt skalar za vektor povzroči vektor.

-In s plezanjem dveh vektorjev je skalar.

Zato glede na vektorje v, ali in W, In poleg tega skalarno λ, je mogoče napisati:

-Vsota vektorjev: v +(ali + W ) = (v + ali) + W

-Skalarni izdelek: λ (v • ali ) = (λv) • ali

Slednje je možno zahvaljujoč kaj v • ali Je skalar in λv Je vektor.

Vendar:

v × (ali × W ) ≠ (v × ali)×W

Polinomna faktorizacija z razvrščanjem izrazov

Ta aplikacija je zelo zanimiva, saj kot je navedeno zgoraj, asociativna lastnina pomaga rešiti določene težave. Vsota monomov je asociativna in to je mogoče uporabiti za upoštevanje, kadar se očiten skupni dejavnik ne pojavi na prvi pogled.

Vam lahko služi: konveksni poligon: definicija, elementi, lastnosti, primeri

Recimo, da se zahteva, da upošteva: x³ + 2x² + 3x +6. Ta polinom nima skupnega dejavnika, vendar poglejmo, kaj se zgodi, če je na ta način razvrščen:

x³ + 2x² + 3x +6 = (x³ + 2x²) + (3x +6)

Prvi oklepaj ima kot skupni dejavnik x²:

x³ + 2x² = x² (x+2)

V drugem je skupni faktor 3:

3x +6 = 3 (x + 2)

Tako:

x³ + 2x² + 3x +6 = x²(x+ 2)+ 3 (x+ 2)

Zdaj obstaja očiten skupni dejavnik, ki je x+2:

x²(x+ 2)+ 3 (x+ 2) = (x+ 2) (x²+3)

Vaje

- Vaja 1

Gradnja šole ima 4 nadstropja, v vsaki pa 12 učilnic s 30 mizami v notranjosti. Koliko miz ima šola skupaj?

Rešitev

Ta problem se rešuje z uporabo asociativne lastnosti množenja, poglejmo:

Skupno število miz = 4 nadstropja x 12 učilnic /tla x 30 miz /učilnica = (4 x 12) x 30 miz = 48 x 30 = 1440 miz.

O Če je prednostno: 4 x (12 x 30) = 4 x 360 = 1440 miz

- Vaja 2

Glede na polinome:

A (x) = 5x³ + 2x² -7x + 1

B (x) = x⁴ +6x³ -5x

C (x) = -8x² +3x -7

Uporabite asociativno lastnost vsote, da najdete (x) + b (x) + c (x).

Rešitev

Prva dva je mogoče razvrstiti in rezultat doda tretji:

A (x) + b (x) = [5x³ + 2x² -7x + 1] + [x⁴ +6x³ -5x] = x⁴ + 11x³+ 2x² -12x +1

Polinom C (x) je takoj dodan:

[x⁴ + 11x³+ 2x² -12x +1] + [-8x² +3x -7] = x⁴ + 11x³ - 6x² -9x -6

Bralec lahko preveri, ali je rezultat enak, če ga rešimo z možnostjo A (x) + [b (x) + c (x)]].

Reference

1. Jiménez, r. 2008. Algebra. Dvorana Prentice.
2. Matematika je zabavna. Komutativni, asociativni in okrožni zakoni. Okreval od: MathisFun.com.
3. Matematično skladišče. Opredelitev asociativne lastnine. Obnovi se od: Mathwarehouse.com.
4. Znanstvenik. Asociativna in komutativna lastnost dodajanja in množenja (s primerom). Okrevano od: Znanstvenik.com.
5. Wikipedija. Asociativna lastnina. Pridobljeno iz: v.Wikipedija.org.