Izjemni izdelki

Kaj so pomembni izdelki?

Pomembni izdelki so algebrske operacije, kjer se izražajo množitve polinomov, ki jih ni treba tradicionalno rešiti, vendar s pomočjo določenih pravil lahko najdemo rezultate istega rezultata.

Polinomi se pomnožijo s tem, ali je mogoče, da imajo veliko izrazov in spremenljivk. Za to, da postopek kratek, se uporabljajo pravila pomembnih izdelkov, ki omogočajo množenje, ne da bi morali iti za termin.

Pomembni izdelki in primeri

Vsak izjemen izdelek je formula, ki je posledica faktorizacije, sestavljene iz polinomov več izrazov, kot so binomi ali trinomiji, imenovani dejavniki.

Dejavniki so osnova moči in imajo eksponent. Ko se dejavniki pomnožijo, je treba dodati eksponente.

Obstaja več pomembnih formul izdelkov, nekatere so bolj uporabljene kot druge, odvisno od polinomov in so naslednje:

Kvadratni binom

Gre za množenje binoma, izraženo v obliki moči, kjer se izrazi dodajo ali odštejejo:

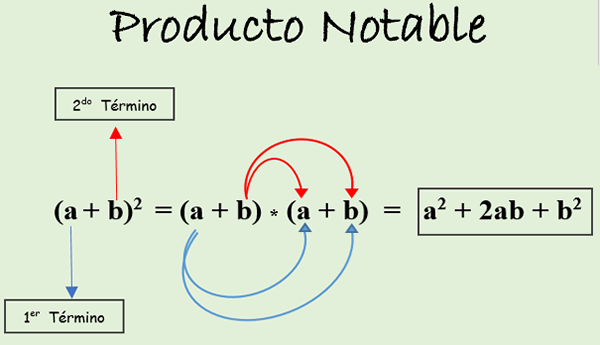
do. Kvadratna vsota Binomial: Je enak kvadratu prvega mandata, poleg tega pa podvoji produkt izrazov in kvadrat drugega mandata. Izraženo je na naslednji način:

(A + B)² = (A + B) _* (A + B).

Na naslednji sliki lahko vidite, kako je izdelek razvit v skladu z omenjenim pravilom. Rezultat se imenuje trinomial popolnega kvadrata.

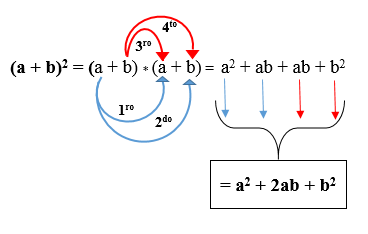
Primer 1

(x + 5) ² = x² + 2 (x * 5) + 5²

(x + 5) ² = x² + 2 (5x) + 25

(x + 5) ² = x² + 10x + 25.

Primer 2

(4a + 2b) = (4a)² + 2 (4 _* 2b) + (2b)²

(4a + 2b) = 8a² + 2 (8ab) + 4b²

(4a + 2b) = 8a² + 16 AB + 4B².

b. Binomial kvadratnega odštevanja: Uporablja se isto pravilo binoma vsote, le da je v tem primeru drugi izraz negativen. Njegova formula je naslednja:

(A - B)² = [(a) + (- b)]²

Vam lahko služi: numerične analogije: vrste, aplikacije in vaje

(A - B)² = a² +2. mesto _* (-b) + (-b)²

(A - B)²   = a² - 2ab + b².

Primer 1

(2x - 6)² = (2x)² - 2 (2x _* 6) + 6²

(2x - 6)²  = 4x² - 2 (12x) + 36

(2x - 6)² = 4x² - 24x + 36.

Konjugacijski izdelek binomalov

Dva binomna sta konjugirana, kadar sta drugi izrazi različnih znakov, torej je prvi pozitiven in drugi negativni ali obratno. Rešeno je z dvigom vsakega monoma in odštetega. Njegova formula je naslednja:

(A + B) _* (A - B)

Na naslednji sliki se razvije produkt dveh konjugiranih binomov, kjer opazimo, da je rezultat razlika v kvadratih.

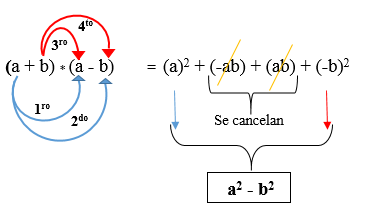
Primer 1

(2a + 3b) (2a - 3b) = 4a² + (-6ab) + (6 Ab) + (-9b²)

(2a + 3b) (2a - 3b) = 4a² - 9b².

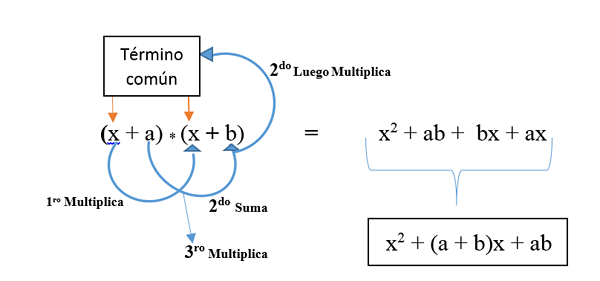
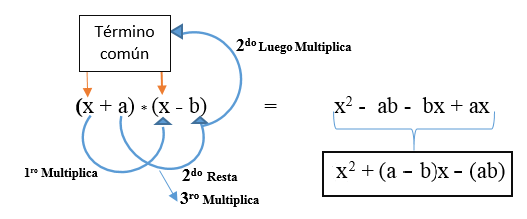
Produkt dveh binomov s skupnim izrazom

Je eden najbolj zapletenih in malo uporabljenih pomembnih izdelkov, saj gre za množenje dveh binomov, ki imata skupni izraz. Pravilo označuje naslednje:

• Kvadrat skupnega izraza.
• Plus vsota izrazov, ki niso pogosti, in jih nato pomnožijo s skupnim izrazom.
• Plus vsota množenja izrazov, ki niso pogosti.

Zastopana je v formuli: (x + a) _* (x + b) in je razvit, kot je prikazano na sliki. Rezultat je neobsežen kvadratni trinomial.

Primer 1

(x + 6) _* (x + 9) = x² + (6 + 9) _* X + (6 _* 9)

(x + 6) _* (x + 9) = x² + 15x + 54.

Obstaja možnost, da je drugi izraz (drugačen izraz) negativen in njegova formula je naslednja: (x + a) _* (x - b).

Primer 2

(7x + 4) _* (7x - 2) = (7x _* 7x) + (4 - 2)_* 7x + (4 _* -2)

(7x + 4) _* (7x - 2) = 49x² + (2)_* 7x - 8

(7x + 4) _* (7x - 2) = 49x² + 14x - 8.

Lahko je tudi, da sta oba različna izraza negativna. Vaša formula bo: (x - a) _* (x - b).

Vam lahko služi: lamy teorem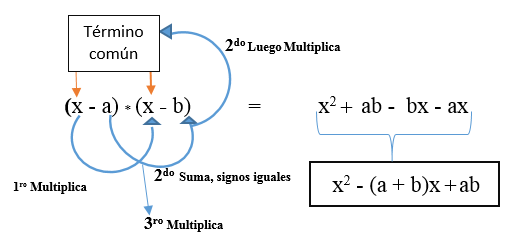

Primer 3

(3B - 6) _* (3b - 5) = (3b _* 3B) + (-6 - 5)_* (3b) + (-6 _* -5)

(3B - 6) _* (3b - 5) = 9b² + (-eleven) _* (3b) + (30)

(3B - 6) _* (3b - 5) = 9b² - 33B + 30.

Kvadratni polinom

V tem primeru obstajata več kot dva izraza in da ga razvijemo, vsak se razreže in doda skupaj z dvakratnim množenjem enega izraza z drugim; Njegova formula je: (A + B + C)² In rezultat operacije je trinomski kvadrat.

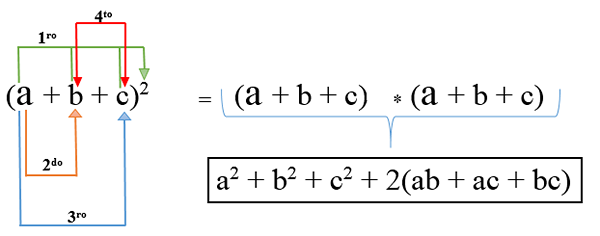
Primer 1

(3x + 2y + 4z)² = (3x)² + (2 in)² + (4z)² + 2 (6xy + 12xz + 8yz)

(3x + 2y + 4z)² = 9x² + 4y² + 16Z² + 12xy + 24xz + 16yz.

Kocka binoma

Je zapleten pomemben izdelek. Da bi ga razvili, se Binom pomnoži s svojim kvadratom, kot sledi:

do. Za binom za kocko vsote:

• Prvi mandat kocka in potroji kvadrat prvega mandata do drugega.
• Plus potroji prvi mandat, drugi kvadrat.
• Plus kocka drugega mandata.

(A + B)³ = (A + B) _* (A + B)²

(A + B)³ = (A + B) _* (do² + 2ab + b²)

(A + B)³ = a³ + 2. mesto²B + AB² + ba² + 2ab² + b³

(A + B)³ = a³ + 3. mesto²B + 3AB² + b³.

Primer 1

(A + 3)³ = a³ + 3 (a)²_*(3) + 3 (a)_*(3)² + (3)³

(A + 3)³ = a³ + 3 (a)²_*(3) + 3 (a)_*(9) + 27

(A + 3)³ = a³ + 9 a² + 27A + 27.

b. Za binom za kocko odštevanja:

• Kocka prvega mandata, razen trojke kvadrata prvega mandata do drugega.
• Plus potroji prvi mandat, drugi kvadrat.
• Manj kocka drugega mandata.

(A - B)³ = (A - B) _* (A - B)²

(A - B)³ = (A - B) _* (do² - 2ab + b²)

(A - B)³ = a³ - 2. mesto²B + AB² - ba² + 2ab² - b³

(A - B)³ = do³ - 3. mesto²B + 3AB² - b³.

Primer 2

(B - 5)³ = b³ + 3 (b)²_*(-5) + 3 (b)_*(-5)² + (-5)³

(B - 5)³ = b³ + 3 (b)²_*(-5) + 3 (b)_*(25) -125

Vam lahko služi: ne -združeni podatki: primeri in rešeni primeri in vaja

(B - 5)³ = b³ - 15b² +75B - 125.

Trinomska kocka

Razvije ga pomnoži po svojem kvadratu. To je zelo obsežen izjemen izdelek, saj se na kocko dvignejo trije izrazi, plus trojko vsakega kvadratnega izraza, pomnoženo z vsakim izrazom, in šestkrat več kot produkt treh izrazov. Videti v boljši obliki:

(A + B + C)³ = (A + b + c) _* (A + B + C)²

(A + B + C)³ = (A + b + c) _* (do² + b² + c² + 2AB + 2AC + 2BC)

(A + B + C)³ = A³ + b³ + c³ + 3. mesto²B + 3AB² + 3. mesto²C + 3ac² + 3b²C + 3BC² + 6ABC.

Primer 1

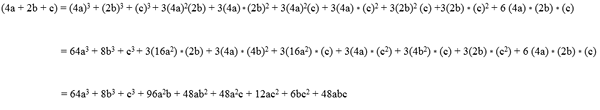
Rešene vaje pomembnih izdelkov

Vaja 1

Razvijte naslednje binom v kocko: (4x - 6)³.

Rešitev

Če se spomnimo, da je binoma na kocki enak prvemu izrazu, dvignjenem na kocko, razen trojke kvadrata prvega mandata do drugega; Plus potroji prvi mandat, z drugim kvadratom, razen kocke drugega mandata.

(4x - 6)³ = (4x)³ - 3 (4x)²(6) + 3 (4x) _* (6)² - (6)²

(4x - 6)³ = 64x³ - 3 (16x²) (6) + 3 (4x)_* (36) - 36

(4x - 6)³ = 64x³ - 288x² + 432x - 36.

Vaja 2

Razvijte naslednje binom: (x + 3) (x + 8).

Rešitev

Imate binom, kjer obstaja skupni izraz, ki je x, drugi izraz. Da bi ga razvili, je treba povečati le skupni izraz, poleg tega vsote izrazov, ki niso pogosti (3 in 8) in jih nato pomnožite s skupnim izrazom, in vsoto množenja izrazov, ki niso pogosti.

(x + 3) (x + 8) = x² + (3 + 8) x + (3_*8)

(x + 3) (x + 8) = x² + 11x + 24.

Reference

1. Angel, a. R. (2007). Elementarna algebra. Pearson Education,.
2. Arthur Goodman, L. H. (devetnajst devetdeset šest). Algebra in trigonometrija z analitično geometrijo. Pearson Education.
3. Das, s. (s.F.). Matematika plus 8. Združeno kraljestvo: Sagar Ratna.
4. Jerome e. Kaufmann, k. L. (2011). Elementarna in vmesna algebra: kombiniran pristop. Florida: Cengage Learning.
5. Pérez, c. D. (2010). Pearson Education.