Koncept verjetnosti frekvence, kako se izračuna in primeri

The Verjetnost frekvence je Pod definicija znotraj preučevanja verjetnosti in njegovih pojavov. Njegova metoda študije glede na dogodke in atribute temelji na velikih količinah ponovitev, tako da dolgoročno opazuje vsako ali celo neskončne ponovitve.

Na primer, Gummitanska ovojnica vsebuje 5 gub vsake barve: modra, rdeča, zelena in rumena. Želite določiti verjetnost, da mora vsaka barva oditi po naključni izbiri.

Dolgočasno si je predstavljati, da bi dobili gumo, jo posneli, vrnili, vzeli gumo in ponovili iste nekaj sto ali več tisočkrat. Vedenje lahko celo želite upoštevati po več milijonih ponovitev.

Nasprotno pa je zanimivo ugotoviti, da po nekaj ponovitvah pričakovana verjetnost 25% ni v celoti izpolnjena, vsaj ne za vse barve po 100 iteracijah.

Po pristopu verjetnosti verjetnosti bo dodelitev vrednosti le s preučevanjem številnih iteracij. Na ta način je treba postopek izvajati in po možnosti registrirati na računalniško ali emuliran način.

Več tokov zavrača verjetnost frekvence in se prepira pomanjkanje empirizma in zanesljivosti v naključnih merilih.

[TOC]

Kako se izračuna verjetnost frekvence?

Ko programirate poskus v katerem koli vmesniku, ki lahko ponuja čisto naključno iteracijo, lahko začnete preučevati frekvenčno verjetnost pojava skozi tabelo vrednosti.

Prejšnji primer je cenjen iz frekvenčnega pristopa:

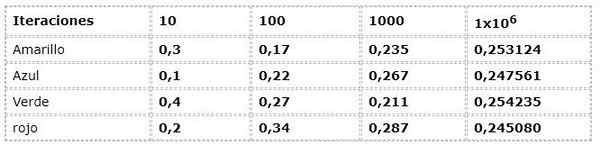
Numerični podatki ustrezajo izrazu:

N (a) = število pojavov/ število ponovitev

Kjer n (a) predstavlja relativno frekvenco dogodka "A"

"A" pripada naboru možnih rezultatov ali vzorčnega prostora ω

Ω: rdeča, zelena, modra, rumena

V prvih iteracijah je veliko razpršenosti, ko se med seboj opazijo frekvence z do 30% razlik, kar je zelo veliko za poskus, ki ima teoretično dogodke z enako možnostjo (Equarobable).

Ko pa ponovitve rastejo, se vrednote vedno bolj zdijo tistim, ki jih predstavlja teoretični in logični tok.

Zakon velikih številk

Kot nepričakovani dogovor med teoretičnimi in frekvenčnimi pristopi se pojavi zakon velikega števila. Kjer se ugotovi, da se vrednosti frekvenčnega eksperimenta po precejšnji količini iteracij približujejo teoretičnim vrednostim.

V primeru lahko opazite, kako se vrednosti približajo 0,250, ko rastejo iteracije. Ta pojav je osnovni v sklepih številnih verjetnostnih del.

Drugi pristopi verjetnosti

Obstajata še dve teoriji ali pristopi k pojem verjetnosti poleg Verjetnost frekvence.

Logična teorija

Vaš pristop je usmerjen v deduktivno logiko pojavov. V prejšnjem primeru je verjetnost pridobitve vsake barve 25% zaprta. Z drugimi besedami.

Subjektivna teorija

Temelji na znanju in prejšnjih prepričanjih, ki jih ima vsak posameznik o pojavih in lastnostih. Izjave, kot so "V svetem tednu vedno dežuje " Upoštevajo vzorec podobnih dogodkov, ki so se zgodili prej.

Zgodovina

Začetki njenega izvajanja izhajajo iz devetnajstega stoletja, ko ga imam v več njenih delu v Cambridgeu Angliji. Toda šele v dvajsetem stoletju sta se razvila in oblikovala 2 statistična matematika Verjetnost frekvence.

Eden od njih je bil Hans Reichenbach, ki svoje delo razvija v publikacijah, kot je "Teorija verjetnosti", objavljeno leta 1949.

Drugi je bil Richard Von Mises, ki je svoje delo temeljito razvil z več publikacijami in predlagal, da bi verjetnost obravnavali kot matematično znanost. Ta koncept je bil nov v matematiki in bi pomenil začetek dobe rasti v preučevanju Verjetnost frekvence.

Pravzaprav je ta dogodek edina razlika s prispevki generacije Venna, Covta in Helma. Kjer verjetnost postane kolega, kot sta geometrija in mehanika.

< La teoría de las probabilidades trata con Ogromni pojavi in ​​ponavljajoči se dogodki. Težave, pri katerih se isti dogodek ponavlja znova in znova, ali pa je hkrati vključenih veliko enotnih elementov> Richard von Mises

Ogromni pojavi in ​​ponavljajoči se dogodki

Tri vrste je mogoče razvrstiti:

• Fizika: obdozni vzorci narave, ki presegajo naključno stanje. Na primer obnašanje molekul elementa v vzorcu.
• Možnost: Njegova temeljna pozornost je naključnost, kot s večkrat sproščanjem kock.
• Biološka statistika: Izbira predmeta preizkusite v skladu z njihovimi značilnostmi in atributi.

V teoriji ima posameznik, ki meri, vlogo pri verjetnostnih podatkih, ker njegovo znanje in izkušnje artikulirajo to vrednost ali napoved.

V Verjetnost frekvence Dogodki bodo obravnavani kot zbirke, ki jih je treba obravnavati, kjer posameznik v oceni ne igra nobene vloge.

Lastnosti

V vsakem elementu se pojavi atribut, ki bo v skladu z naravo tega spremenljiv. Na primer, v vrsti fizikalnih pojavov bodo molekule vode imele različne hitrosti.

Pri izstrelitvi kocke poznamo vzorčni prostor ω, ki predstavlja atribute poskusa.

Ω: 1, 2, 3, 4, 5, 6

Obstajajo tudi drugi atributi, kot je ω_Str  Ali pa čuden ω_Yo

Ω_str : 2, 4, 6

Ω_Yo : 1, 3, 5

Ki jih je mogoče opredeliti kot ne -elementarni atributi.

Primer

• Želite izračunati frekvenco vsake možne vsote pri zagonu dveh kock.

Za to je poskus programiran, kjer sta v vsaki iteraciji dodana dve naključni vrednosti med [1, 6].

Podatki so zabeleženi v tabeli, trendi v velikem številu.

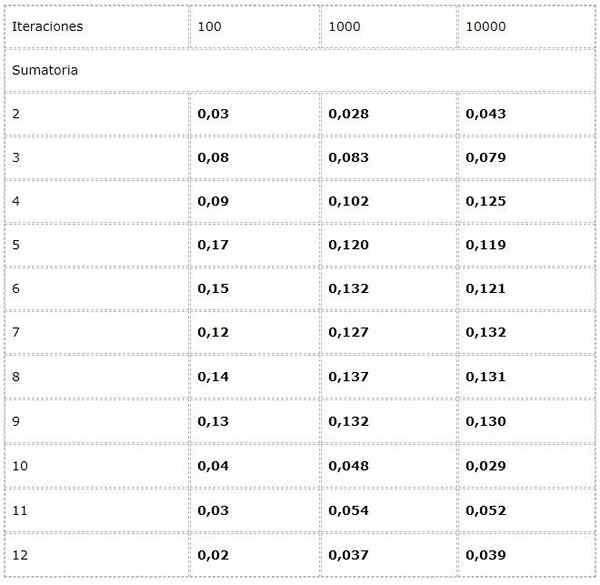
Opazimo, da se rezultati lahko med ponovitvami znatno razlikujejo. Vendar je zakon velikega števila viden v navidezni konvergenci, predstavljeni v zadnjih dveh stolpcih.

Reference

1. Statistika in ocena dokazov za forenzične znanstvenike. Druga izdaja. Colin G.G. Aitken. Šola matematike. Univerza v Edinburghu v Veliki Britaniji
2. Matematika za računalništvo. Eric Lehman. Google inc.
   F Thomson Leighton Ministrstvo za matematiko in računalništvo in laboratorij AI, Massachussetts Institute of Technology; Akamai Technologies
3. Aritmetični učitelj, letnik 29. Nacionalni svet učiteljev matematike, 1981. Univerza v Michiganu.
4. Teorija učenja in poučevanja: Raziskave kognicije in pouka / urejal Stephen R. Campbell in Rina Zazkis. ABLECX Publishing 88 Post Road West, Westport CT 06881
5. Bernoulli, J. (1987). Ars uveljavljandi- 4ème partie. ROUEN: IREM.