Heptagonalna prizma
- 4372
- 1230
- Roman Schamberger
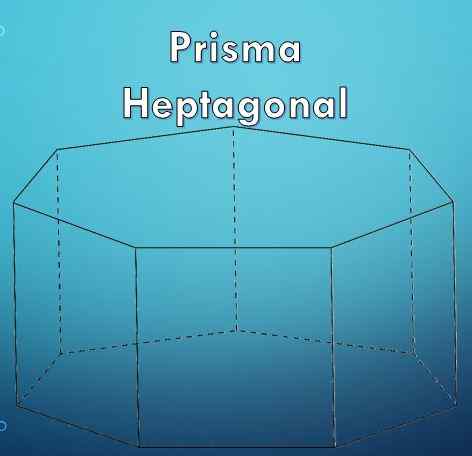
 Heptagonalna prizma ima 7 strani
Heptagonalna prizma ima 7 strani Kaj je heptagonalna prizma?
A Heptagonalna prizma To je geometrijska figura, ki, kot že ime pove, vključuje dve geometrijski definiciji, ki sta: Prizma in Heptagon. "Prizma" je omejena geometrijska številka dveh podstavkov, ki sta enaki in vzporedni poligoni, njihovi stranski obrazi pa so paralelogrami.
"Heptagon" je poligon, ki ga tvori sedem (7) strani. Ker je heptagon poligon, je lahko reden ali nepravilen.
Poligon naj bi bil reden, če imajo vse njihove strani enake dolžine in njihovi notranji koti merijo enako, imenujejo tudi enakostranični poligoni; Sicer se reče, da je poligon nepravilen.

Značilnosti heptagonalne prizme
Spodaj so določene značilnosti, ki imajo heptagonalno prizmo, kot so: njena konstrukcija, lastnosti njegovih baz, območje vseh obrazov in glasnost.
1- Gradnja
Za izgradnjo heptagonske prizme sta potrebna dva heptagona, ki bosta njene baze in sedem paralelogramov, po en na vsaki strani Heptagona.
Začne risati heptagon, nato pa je narisanih sedem navpičnih črt, enake dolžine.
Končno je narisan še en heptagon, da njeni točki sovpadajo s koncem vrstic, narisanih v prejšnjem koraku.
Heptagonalna prizma, ki je bila prej narisana, se imenuje ravna heptagonalna prizma. Lahko pa imate tudi poševno heptagonalno prizmo, kot je naslednja slika.
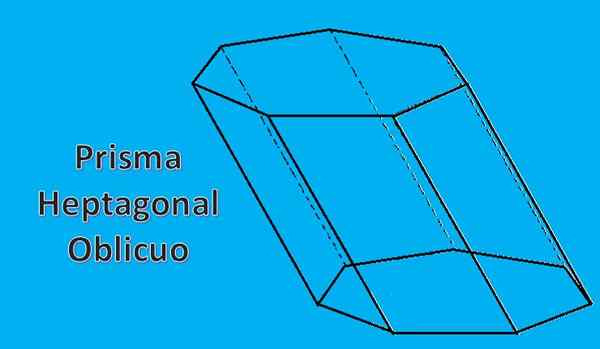
2- lastnosti njegovih baz
Ker so njihove baze heptogoni, izpolnjujejo, da je diagonalna številka d = nx (n-3)/2, kjer je "n" število strani poligona; V tem primeru morate d = 7 × 4/2 = 14.
Vam lahko služi: kaj so trikotne številke? Lastnosti in demonstracijeVidimo tudi, da je vsota notranjih kotov katerega koli heptagona (običajnega ali nepravilnega) enakih 900 °. To lahko preverite z naslednjo sliko.
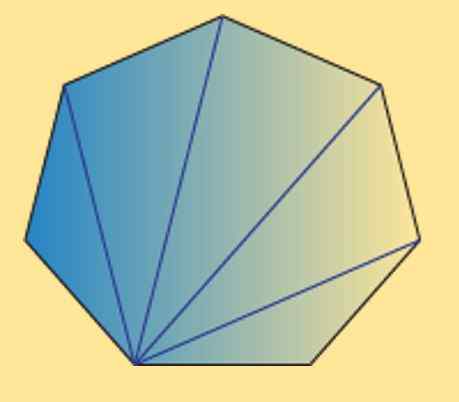
Kot je razvidno, obstaja 5 notranjih trikotnikov in uporaba vsote notranjih kotov trikotnika je enaka 180 °, lahko dobimo, da želeni rezultat.
3- območje, potrebno za izgradnjo heptagonalne prizme
Ker sta njeni bazi dva heptogona in njene strani paralelogram.

V tem primeru se bo izračunalo območje običajnega heptagona. Za to je pomembno vedeti definicijo apotema.
Apotheme je pravokotna črta, ki sega od središča navadnega poligona do sredine katere koli strani.
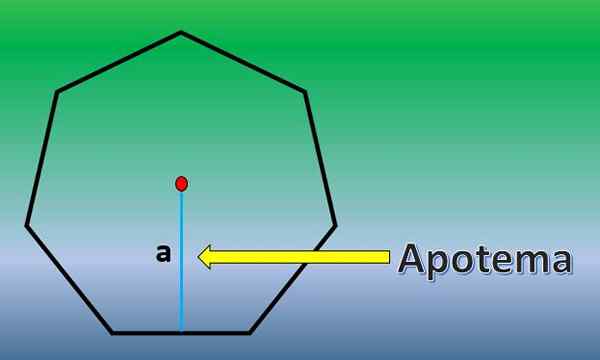
Ko je apotema znan, je območje Heptagona H = 7xlxa/2, kjer je "L" dolžina vsake strani in "A" dolžina apotema.
Območje paralelograma je enostavno izračunati, opredeljeno je kot p = lxh, kjer je "l" enaka dolžina strani heptagona in "h" je višina prizme.
Za zaključek je količina materiala, potrebnega za izgradnjo heptagonalne prizme (z običajnimi osnovami), 7xlxa+7xlxh, torej 7xl (a+h).
4- Volumen
Ko je znana površina baze in višina prizme, je prostornina definirana kot (osnovno območje) x (višina).
V primeru heptagonalne prizme (z redno osnovo) mora biti v = 7xlxaxh/2; Lahko ga zapišemo tudi kot v = pxaxh/2, kjer je "p" obod običajnega heptagona.
Vam lahko služi: kakšni so delitve 30? (Pojasnilo)
