Fizično

Načelo prenosljivosti sil

Načelo prenosljivosti sil

Pojasnjujemo, kaj je načelo prenosljivosti, s primeri in reševanimi vajami

Kaj je načelo prenosljivosti?

On Načelo prenosljivosti Velja za trdne predmete in potrjuje, da je uporabljena sila na neki točki telesa enakovredna drugi sili enake velikosti in smeri, dokler se na isti črti uporablja omenjena sila, ki vsebuje prvotno silo.

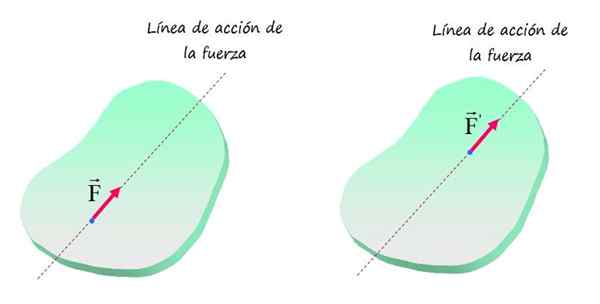
Zato bo vsaka sila enake razsežnosti in smeri povzročila enak učinek translacijskega in rotacijskega gibanja na objekt, pod pogojem, da je njegova točka uporabe na isti črti, kot je prikazano na naslednji sliki.

V togi telesu učinek sile ni spremenjen, ko se njegova točka uporabe premika po njegovi liniji. Vir: f. Zapata.

Prikazane sile F in F'Rečeno je, da so enakovredne sile in nenadna ravna črta, ki jih vsebuje silna akcijska linija.

Načelo prenosljivosti je zelo koristno, saj omogoča udobje sil, ki delujejo na predmet, da bi olajšali analizo.

Pojasnilo Načelo prenosljivosti

Načelo prenosljivosti temelji na dejstvu, da dve sili F1 in F2 So enakovredni, pod pogojem, da imajo enako velikost in isto smer.

Poleg tega morajo ustvariti isti trenutek glede na katero koli točko ali, kar je zagotovljeno z isto linijo delovanja in ker je trenutek produkt sile do razdalje ali omenjene črte.

Upoštevajte, da načelo velja samo za togo telo, to je predmet, v katerem se relativne razdalje med njihovimi deli ne spreminjajo, ker so notranje sile, ki ga ohranjajo v koheziji. Zato predmet ne spremeni svoje oblike, ne glede na to, ali te zunanje sile delujejo.

Po drugi strani pa, če predmet ni tog, bi spreminjanje točke uporabe sil povzročile spremembe v smislu napetosti ali stiskanja, ki se uporabljajo za telo, kar bi privedlo do sprememb v njegovi obliki.

Seveda predpostavimo, da je telo togo, ni nič drugega kot idealizacija, saj so v resnici vsi predmeti deformabilni v večji ali manjši meri. Vendar je v mnogih primerih odličen pristop, če je deformacija dovolj majhna, da se lahko šteje.

Omejitve

Načelo prenosljivosti je, kot je navedeno, omejitev glede notranjih učinkov streljanja ali drsenja sil. Na naslednji sliki je prikazan predmet s silami F in F'Uporablja se v različnih točkah iste akcijske linije.

Vam lahko služi: Načelo Archimedes: formula, demonstracije, aplikacije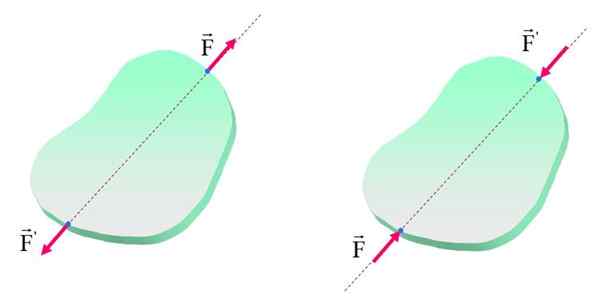Načelo prenosljivosti je uporabno le v togih telesih, saj spreminjanje točke uporabe sil lahko povzroči različne učinke na deformabilna telesa. Vir: f. Zapata.

Upoštevajte, da je na obeh slikah telo (togo ali ne) v ravnovesju, ker imajo sile enako velikost in smer in nasprotna čutila. Poleg tega so sile, kot rečeno, na isti liniji delovanja, na levi sliki.

Čeprav telo ostane v mirovanju, so notranji učinki različni in postanejo patentni, če predmet ni povsem tog. V primeru leve sile ponavadi iztegnejo telo, na desni pa ga ponavadi skrajšajo.

Primeri Načelo prenosljivosti

Primer 1

Recimo, da imate težko prtljažnik na vodoravnem tleh. Učinek potiskanja na levo stran je enak, kot če je ravna. V tem primeru je gibanje prtljažnika na tleh enako.

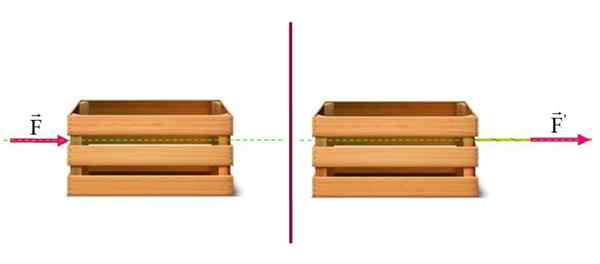Učinek potiskanja ali vlečenja predala na vodoravno površino je enak: premaknite ga od leve proti desni. Vir: f. Zapata.

Primer 2

Imate dolgo desko kot polica. Za namestitev je enakovreden.

V obeh primerih bodo sile, ki uravnotežijo plošča.

Načelo prenosljivosti in trenutki

Recimo, da je v točki A uporabljena sila F, trenutek, ki izvira iz te sile okoli točke ali prikazano na sliki, je:

MTudi = rDo × F

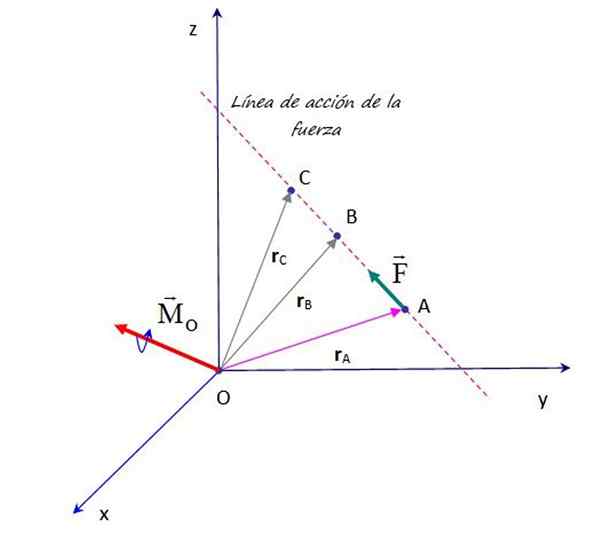Sila drsnika ali prenosa vzdolž njegove delovne linije ne spreminja trenutka, ko se izvaja na točki oz. Vir: f. Zapata.

No, načelo prenosljivosti zagotavlja, da to zagotavlja F, Delovanje na kateri koli točki vzdolž svoje akcije, na primer točke B, C in več, izvira iz istega trenutka glede na točko oz. Zato je veljavno potrditi, da:

MTudi = rDo × F  = rB × F = rC × F

Rešene vaje

Vaja 1

Homogena krogla ima maso M = 5 kg in počiva na vodoravni površini brez trenja.

    • a) Narišite v shemo, ki jo ima površina na krogli.
    • b) Zgradite brezplačni karoserijski diagram krogle
    • c) Izračunajte vrednost normalne sile, ki jo ima površina na krogli.

  • Rešitve A in B

V grafu) je prikazana sila, ki jo ima površina na krogli, imenovana normalno N, Ker je pravokotno na površino. Točka uporabe sile sovpada s podporno točko krogle na površini (točka v zeleni barvi) in linija delovanja je navpična, ki poteka skozi geometrijsko središče krogle.

Vam lahko služi: Zemljina magnetosfera: značilnosti, struktura, plini

V grafu B) Obstaja prosti karoserijski diagram krogle, kjer je poleg običajnega prikazana teža, ki se uporablja v težišču, označena z rumeno točko.

Zahvaljujoč načelu prenosljivosti, normalna sila N Lahko ga prenesemo na to točko, ne da bi spremenil svoje učinke na kroglo. Ti učinki niso drugi, ki ohranjajo sfero podprto na mizi v ravnovesju.

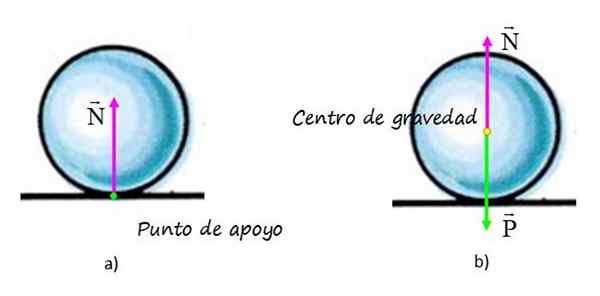Na sliki a) na levi strani normalno deluje na podporni točki krogle s površino. Na sliki b) se na prostem telesnem diagramu normalno prenese v težišče, saj je navpična njegova linija delovanja. Njeni učinki niso spremenjeni, ker uravnoteži težo, tako da je krogla v ravnovesju. Vir: f. Zapata.

  • Rešitev c

Ker je sfera v ravnovesju, saj je kot pozitiven smisel navpična in negativna navpična navzdol, Newtonov drugi zakon ima za posledico:

N - p = 0

To pomeni, da sta teža in normalna uravnotežena, zato sta po velikosti enaka:

N = p = mg = 5kg × 9.8 m/s2 = 49 N, usmerjeno navpično navzgor.

Vaja 2

Navedite, ali je v naslednjih primerih izpolnjeno načelo prenosljivosti:

  • Prvi primer

Sila 20 N vodoravno, nanesena na togo telo, nadomesti druga sila 15 N, nanesena na drugi točki na telesu, čeprav se oba uporabljata v isti smeri.

    • Rešitev

V tem primeru načelo prenosljivosti ne bo izpolnjeno, čeprav se obe sili uporabljata v isti smeri, druga sila nima enake velikosti kot prva. Zato ni podan eden od nepogrešljivih pogojev načela prenosljivosti.

  • Drugi primer

Sila 20 N vodoravno, nanesena na togo telo, nadomesti še en od 20 N, nanesena na drugi točki telesa in navpično.

    • Rešitev
Vam lahko služi: Planck Constant: Formule, vrednosti in vaje

Ob tej priložnosti načelo prenosljivosti ni izpolnjeno, čeprav imata obe sili isti modul, ne veljata v isti smeri. Spet ni podan eden od nepogrešljivih pogojev načela prenosljivosti. Lahko rečemo, da sta obe sili enakovredni.

  • Tretji primer

Sila 10 N se spreminja vodoravno na togo telesu, ki se uporablja tudi na drugo točko telesa, vendar v isti smeri in pomenu.

    • Rešitev

V tem primeru je izpolnjeno načelo prenosljivosti, saj sta obe sili enake velikosti in se uporabljata v isti smeri in pomenu. Izpolnjeni so vsi potrebni pogoji načela prenosljivosti. Lahko rečemo, da sta obe sili enakovredni.

  • Četrti primer

Sila je drseta v smeri vaše akcijske črte.

    • Rešitev

V tem primeru se načelo prenosljivosti izpolnjuje, saj se z isto silo razsežnost uporabljene sile ne razlikuje in zdrsne v svojo akcijsko črto. Ponovno so izpolnjeni vsi potrebni pogoji načela prenosljivosti.

Vaja 3

Na togi telesu veljata dve zunanji sili. Obe sili se uporabljata v isti smeri in v isto smer. Če je prvi modul 15 N in drugi od 25 N, kakšni pogoji naj tretji zunanji sili, ki nadomestijo rezultat prejšnjih dveh, da bi dosegli načelo prenosljivosti?

  • Rešitev

Po eni strani mora biti vrednost nastale sile 40 N, kar je rezultat dodajanja modula obeh sil.

Po drugi strani mora nastala sila delovati kjer koli v ravni črti, ki se pridruži obema točkama uporabe obeh sil.

Reference

  1. Bedford, 2000. Do. Mehanika za inženiring: statična. Addison Wesley. 
  2. Pivo, f. 2010. Vektorska mehanika za inženirje. McGraw Hill. 5. Izdaja.
  3. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6. Ed Prentice Hall.
  4. Hibbeler, R. 2004. Inženirska mehanika: statika. Dvorana Prentice.
  5. Meriam, j.L. 2012. Inženirska mehanika: statika. 7. izdaja. Wiley & Sons.