Zgodovina, aplikacije, primeri velikonočnega načela

On Načelo Pascal, o Pascal Law ugotovi, da se sprememba tlaka tekočine, omejene v kateri koli od njegovih točk, prenaša brez sprememb na vse druge točke znotraj tekočine.

To načelo je odkril francoski znanstvenik Blaise Pascal (1623 - 1662). Zaradi pomena prispevkov, ki jih je Pascal prispeval k znanosti.

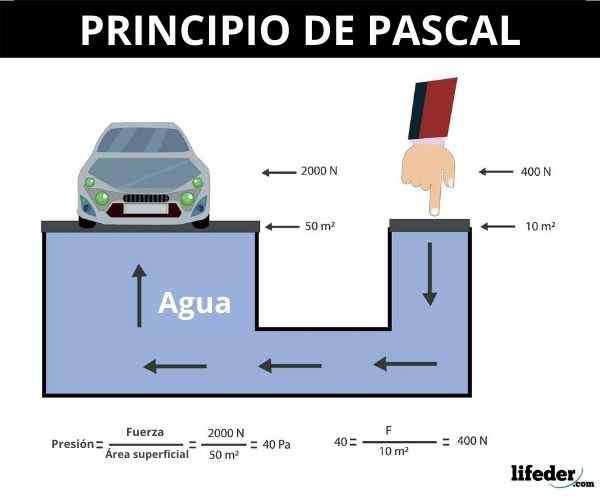
Ker je tlak opredeljen kot količnik med silo, pravokotno na območje med njenim območjem, je 1 Pascal (PA) enak 1 Newtonu / M².

[TOC]

Zgodovina

Da bi preveril svoje načelo, je Pascal zasnoval precej preveliko demonstracijo. Vzel je votlo kroglo in preboden na več mestih, dal kape v vse luknje, razen v enem, za kar jo je napolnil z vodo. V tem je postavil brizgo, ki je bila zagotovljena z batom.

Z zadostnim povečanjem tlaka v batu se zgornje meje ustrelijo hkrati, ker se tlak prenaša enako na vse točke tekočine in v vse smeri, s čimer prikazuje zakon Pascala.

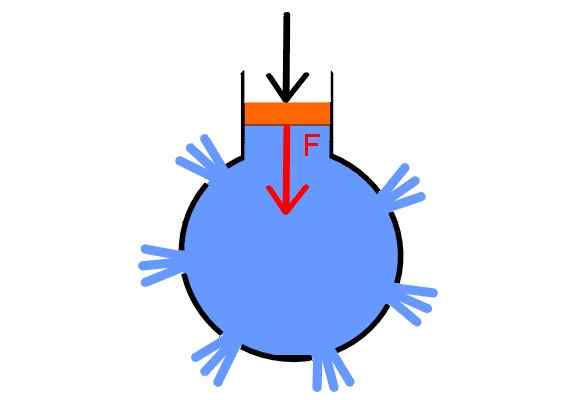Pascal brizgo. Vir: Wikimedia Commons.

Blaise Pascal je imel kratko življenje, ki jo je zaznamovala bolezen. Neverjeten doseg njegovega uma ga je pripeljal do raziskovanja v različnih vidikih narave in filozofije. Njegovi prispevki niso bili omejeni na preučevanje vedenja tekočin, Pascal je bil tudi pionir računalništva.

In pri 19 letih je Pascal ustvarila mehanski kalkulator, da jo je oče uporabil pri svojem delu v francoskem davčnem sistemu: The Pascalina.

Tudi s prijateljem in kolegom Velikim matematikom Pierrom iz Fermata je oblikoval teorijo verjetnosti, nepogrešljivo v fiziki in statistiki. Pascal je umrl v Parizu, v starosti 39 let.

Pojasnilo načela Pascal

Naslednji poskus je precej preprost: U cev je napolnjena z vodo in na vsakem koncu so nameščeni pokrovčki, ki lahko gladko in enostavno drsijo kot bat. Tlak proti levemu batu se nekoliko potopi in opazimo, da se tisti na desni dviga, ki ga potisne tekočina (spodnja številka).

Vam lahko služi: Andromeda: odkritje, izvor, značilnosti, struktura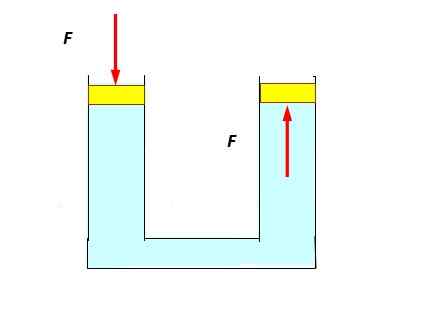Uporaba načela Pascal. Vir: Self Made.

To se zgodi, ker se tlak prenaša brez zmanjšanja na polno točko tekočine, vključno s tistimi, ki so v stiku z desnim batom.

Tekočine, kot sta voda ali olje, so nestisljive, hkrati pa imajo molekule dovolj svobode gibanja, kar omogoča, da se pritisk porazdeli na desni bat.

Zahvaljujoč temu desni bat prejme silo, ki je popolnoma enaka po velikosti in smeri, v katero je bila nanesena na levo, vendar v nasprotni smeri.

Tlak v statični tekočini je neodvisen od oblike posode. Takoj bo dokazano, da se tlak linearno spreminja glede na globino in načelo Pascala je posledica tega.

Sprememba tlaka v kateri koli točki naredi tlak na drugi točki v isti količini. V nasprotnem primeru bi obstajal dodaten tlak, ki bi tekel tekočino.

Razmerje med pritiskom in globino

Tekočina za počitek prinaša silo na stenah posode, ki jo vsebuje, in tudi na površini katerega koli predmeta, potopljenega v njega. V eksperimentu Pascal brizgo je razvidno, da izhaja vodna mreža pravokotno Na kroglo.

Tekočine porazdelijo silo pravokotno na površini, na kateri deluje, zato je priročno uvesti koncept povprečnega tlaka Str_m Kot je izvajala pravokotna sila F_⊥ Po območju Do, katere enota je Pascal:

Str_m = F_⊥ / Do

Tlak se poveča z globino. Ogledate si lahko majhen del statične ravnotežne tekočine in uporabite Newtonov drugi zakon:

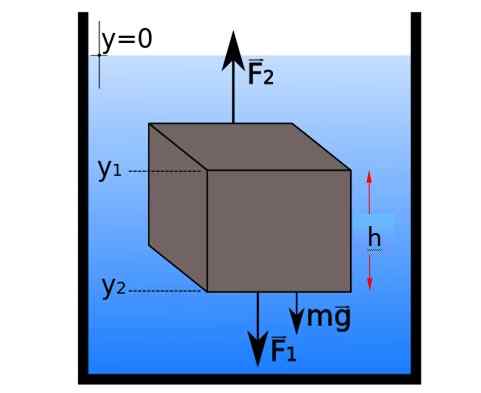Prosti karoserijski diagram majhnega dela statičnega ravnovesja z v obliki kocke. Vir: E-XUAO [CC BY-SA 4.0 (https: // creativeCommons.Org/licence/by-sa/4.0)]

Vodoravne sile prekličejo pari, v navpični smeri pa so sile razvrščene na naslednji način:

∑f_in = F₂ - F₁ - mg = 0 → F₂ - F₁ = mg

Izražanje testa v smislu gostote ρ = masa /volumna:

Str₂.A- p₁.A = ρ X prostornina x g

Prostornina del tekočine je izdelek pri x H:

Lahko vam služi: drugi zakon termodinamike: formule, enačbe, primeri

Do.(P₂ - Str₁) = ρ X a x h x g

ΔP = ρ.g.h   Temeljni teorem hidrostatičnega

Prijave

Backhoe uporablja načelo Pascal za dvigovanje velikih pesosov

Načelo Pascal je bilo uporabljeno za izgradnjo številnih naprav, ki pomnožijo moč in olajšajo naloge, kot so dviganje pesosov, žigosanje na kovini ali stiskalnimi predmeti. Med njimi so:

-Hidravlična stiskalnica

-Avtomobilski zavorni sistem

-Mehanske lopate in mehanske roke

-Hidravlična mačka

-Žerjavi in ​​dvigala

Nato poglejmo, kako načelo Pascal naredi majhne sile v velike sile, da opravljajo vsa ta dela. Hidravlični tisk je najbolj značilen primer in bo analiziran spodaj.

Hidravlična stiskalnica

Za izgradnjo hidravlične stiskalnice se vzame ista naprava zgornje figure, to je v zabojniku v obliki črke, za katero že vemo, da se ista sila prenaša iz enega bata. Razlika bo velikost batov in zaradi tega je naprava delovala.

Naslednja slika prikazuje načelo Pascala v akciji. Tlak je enak na vseh točkah tekočine, tako v majhnem kot v velikem batu:

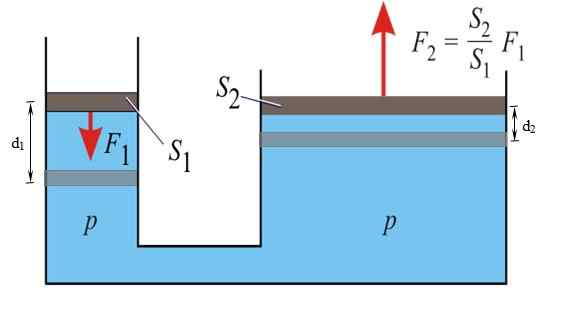Shema hidravličnega tiska. Vir: Wikimedia Commons.

p = f₁ / S₁ = F₂ / S₂

Obseg sile, ki se prenaša na velik bat, je:

F₂ = (S₂ / S₁). F₁

Kot s₂ > S₁, rezultate v f₂ > F₁, Zato se je izhodna sila pomnožila v faktorju, ki ga daje količnik med območji.

Primeri

Ta razdelek prikazuje primere prijave.

Hidravlične zavore

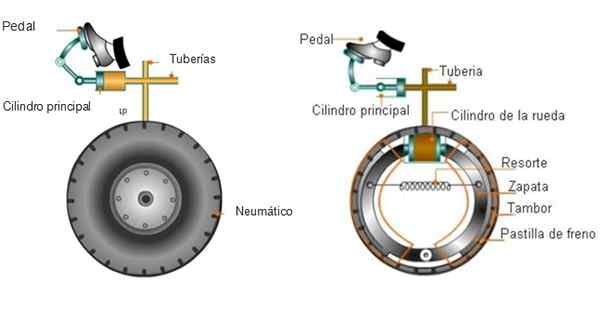
Avtomobilske zavore uporabljajo načelo Pascal skozi hidravlično tekočino, ki napolni nekaj cevi, povezanih s kolesi. Ko se morate ustaviti, voznik uporabi silo tako, da zatira zavorno stopalko in povzroči pritisk na tekočino.

Na drugem koncu pritisk potisne zavorne ploščice na bobne ali zavorne diske, ki se obrnejo skupaj s kolesi (ne z pnevmatikami). Nastalo trenje se disk ustavi, prav tako upočasni kolesa.

Vam lahko služi: mehanski valovi: značilnosti, lastnosti, formule, vrsteHidravlični zavorni sistem. Vir: f. Zapata

Mehanska prednost hidravlične stiskalnice

V hidravlični stiskalnici spodnje številke mora biti vhodna dela enaka izhodnemu delu, dokler se trenje ne upošteva.

Vhodna sila F₁ naredi, da bat potuje na daljavo d₁ Ko se spustite, medtem ko izhodna sila F₂ Omogoča d₂ bata, ki gre navzgor. Če je mehansko delo obeh sil enako:

F₁.d₁ = F₂. d₂

Mehanska prednost M je količnik med velikostmi vhodne in izhodne sile:

M = f₂/F₁ = d₁/d₂

In kot je prikazano v prejšnjem razdelku, se lahko izrazi tudi kot količnik med območji:

F₂/F₁ = S₂ / S₁

Zdi se, da je delo opravljeno brezplačno, vendar s to napravo v resnici ne ustvarja energije, saj je mehanska prednost pridobljena na račun premika majhnega bata D₁.

Torej za optimizacijo zmogljivosti v napravo dodamo sistem ventila tako, da se izhodni bat dvigne zahvaljujoč kratkim impulzom na vhodnem batu.

Na ta način upravljavec garažnih hidravličnih črpalk večkrat, da postopoma dvigne vozilo.

Vaja rešena

V hidravlični stiskalnici slike 5 so območja batov 0.5 kvadratnih centimetrov (majhen bat) in 25 kvadratnih centimetrov (velik bat). Najti:

a) Mehanska prednost te stiskalnice.

b) potrebna sila za dvig obremenitve 1 tone.

c) razdalja, na kateri mora vhodna sila delovati, da dvigne omenjeno obremenitev v 1 palcu.

Izrazite vse rezultate v enotah britanskega sistema in mednarodnega sistema, če.

Rešitev

a) Mehanska prednost je:

M = f₂/F₁ = S₂/S₁ = 25 in² / 0.5 v² = 50

b) 1 tona enakovredna 2000 lb-sili. Potrebna moč je f₁:

F₁ = F₂ / M = 2000 lb-sil / 50 = 40 lb sil

Za izražanje rezultata v mednarodnem sistemu je potreben naslednji faktor pretvorbe:

1 lb-sila = 4.448 n

Zato je velikost F1 177.92 n.

c) M = d₁/d_{2 →} d₁ = M.d₂ = 50 x 1 in = 50 in

Potreben faktor pretvorbe je: 1 in = 2.54 cm

d₁ = 127 cm = 1.27 m

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill. 417-450.
2. Fizika na fakulteti. Pascal's principa. Okrevano od: OpenTextbc.AC.
3. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 4. Tekočine in termodinamika. Uredil Douglas Figueroa (USB). 4 - 12.
4. Rex, a. 2011. Osnove fizike. Pearson. 246-255.
5. Tippens, str. 2011. Fizika: pojmi in aplikacije. 7. izdaja. McGraw Hill.301-320.