Archimedes načela formula, demonstracije, aplikacije

On Načelo Archimeda Pravi, da popolnoma ali delno potopljeno telo prejme navpično silo pritisk, ki je enakovredna teži volumna tekočine, ki jo telo premika. 

Nekateri predmeti lebdijo v vodi, drugi se potopijo in nekateri se delno potopijo. Če želite potopiti kroglico na plaži, se je treba potruditi, ker se ta sila takoj zazna, da jo poskuša vrniti na površje. Namesto tega kovinska krogla hitro potopi. 

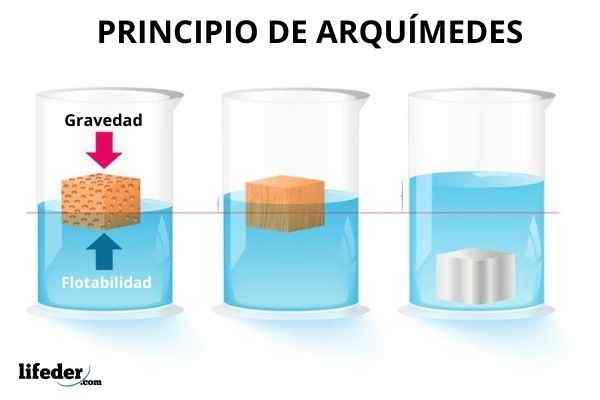
Po drugi strani se zdijo potopljeni predmeti lažji, zato obstaja sila, ki jo izvaja tekočina, ki nasprotuje teži. Vendar sploh ne morete nadomestiti gravitacije. In čeprav je bolj razvidno z vodo, lahko plini ustvarijo tudi to silo na potopljenih predmetih v njih.

[TOC]

Zgodovina

Arhimedi iz Sirakuze (287-212 a. C.) To je moral odkriti to načelo, saj je bil eden največjih znanstvenikov v zgodovini. Pravijo, da je kralj Hierón II iz Syracuse poslal zlatoga zlata, da bi izdelal novo krono, za katero mu je izročil določeno količino zlata.

Arhimedi

Ko je kralj prejel novo krono, je imel pravo težo, vendar je sumil, da ga je zlati zlati varal z dodajanjem srebra namesto zlata. Kako bi ga lahko preveril, ne da bi uničil krono?

Hierón je poklical Archimedes, čigar slava učenjaka je bila dobro znana, da bi mu pomagal rešiti težavo. Legenda zatrjuje, da je bil Archimedes potopljen v kad, ko je našel odgovor in takšno je bilo njegovo čustvo, da je tekel goli po ulicah Sirakuze, da bi iskal kralja, ki kriči "Eureka", kar pomeni, da "sem ga našel".

https: // giphy.com/gifs/stito3echtlnbvliz3

Kaj je našel Archimedes? No, ko je v kopalnici vzel kopalnico v kadi, ko je vstopil, kar pomeni, da potopljeno telo izpodriva določeno količino tekočine.

In če sem krono potopil v vodo, je moral premikati tudi določeno količino vode, če je krona izdelana iz zlata in drugačna, če je bila narejena iz zlitine s srebrom.

Načela Archimedes

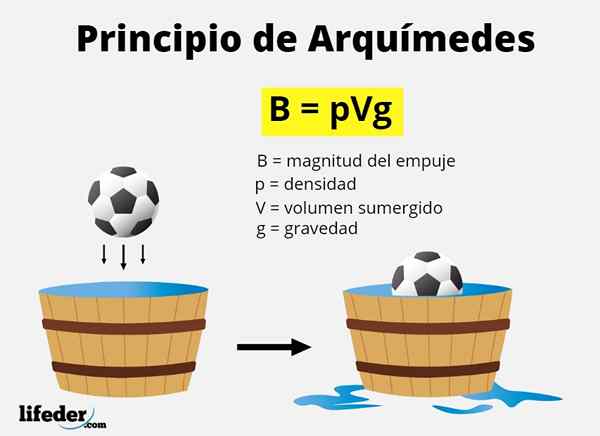
Promocijske sile, omenjene v načelu Archimedes pritisk hidrostatični tudi Flotacijska sila In, kot smo rekli, je enakovredna teži volumna tekočine, ki jo telo premika.

Razsežen prostornina je enakovredna količini predmeta, ki je potopljen, bodisi v celoti ali delno. Ker je teža karkoli mg, In masa tekočine je Gostota X Volume, Zanika, kako je B do razsežnosti potiska, matematično mora:

B = m_tekoče x g = gostota tekočine x potopljena volumen x gravitacija

B = ρ_tekoče x v_potopljeno x g

Kjer grško pismo ρ ("rho") označuje gostoto.

Navidezna teža

Teža predmetov se izračuna z dobro znanim izrazom mg, Vendar se stvari počutijo lažje, ko so potopljene v vodo. 

On očitna teža objekta je tisto, kar ima, ko je potopljen v vodo ali drugo tekočino in če ga poznate, lahko pridobite količino nepravilnega predmeta, kot je krona kralja Hieróna, kot bo razvidno spodaj.

Vam lahko služi: 13 primerov Newtonovega prvega zakona v resničnem življenju

Če želite to narediti, je popolnoma potopljen v vodo in podvržen vrvi, pritrjeni na a dinamometer -instrument, ki je opremljen z vzmetjo, ki služi za merjenje sil-. Večja je teža predmeta, večja je raztezanje vzmeti, ki se meri na lestvici, ki je navedena v napravi.

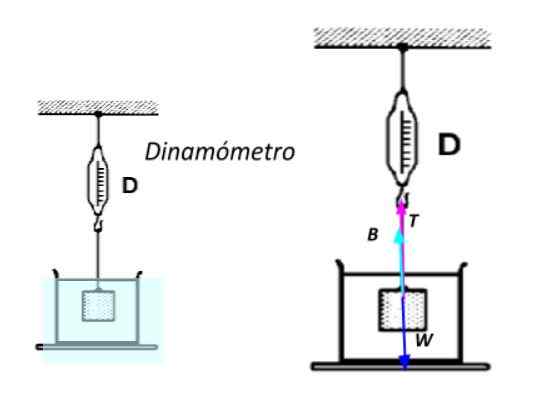Očitna teža potopljenega predmeta. Vir: Pripravil F. Zapata.

Uporaba Newtonovega drugega zakona, ki ve, da je predmet v mirovanju:

Σf_in = B + T - W = 0

Navidezna teža w_do Je enakovreden napetosti na vrvi:

T = w_do

W_do = mg - ρ_tekoče . V. g

Če je potreben potopljeni volumen V, se očisti kot:

V = (w - w_do ) / ρ_tekoče  . g

Demonstracija

https: // giphy.com/gifs/mcphppgnpbhl4cgaq

Ko telo potopi, je potisk, ki je posledica vseh sil, ki se na telesu izvajajo skozi tlak, ki ga povzroča okoliška tekočina:

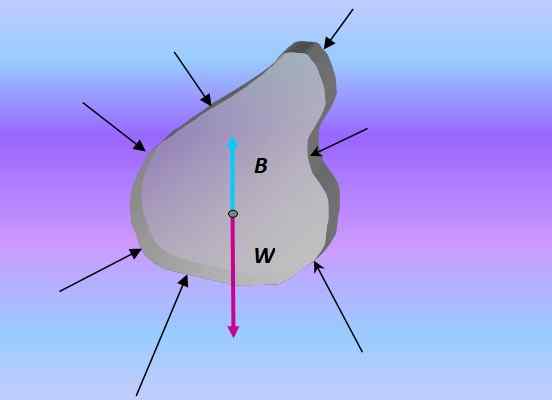Brezplačni karoserijski diagram potopljenega predmeta. Vir: Pripravil F. Zapata.

Pritisk in globina

Ker se tlak poveča z globino, je rezultat teh sil vedno usmerjen navpično navzgor. Zato je načelo Archimeda posledica temeljnega teorema hidrostatika, ki navaja tlak P, ki ga izvaja tekočina z globino z kot:

P = ρ.g.z

Sile na statično ravnotežno tekočino

Da bi pokazali načelo Archimedes, se v mirovanju vzame majhen cilindrični počitek, da analizira sile, ki so na njem, kot je prikazano na naslednji sliki. Sile na ukrivljeni površini valja se prekličejo med seboj. 

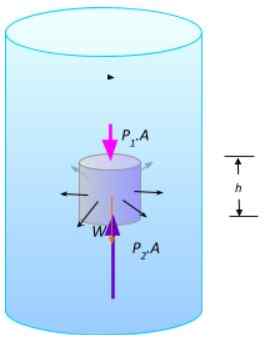Del tekočine v ravnovesju. Vir: Pripravil F. Zapata.

Velike navpičnih sil so F₁ = Str₁.A in F₂ = P2.A, obstaja teža W. Ker je tekočina v ravnovesju, je treba vsoto sil preklicati:

∑f_in = P₂.A- p₁.A- w = 0

Str₂.A- p₁.A = w

Ker potisk kompenzira na težo, saj je del tekočine v mirovanju, potem:

B = str₂.A- p₁.A = w

Iz tega izraza izhaja, da je potisk posledica razlike v tlakih med zgornjo stranjo valja in spodnjim. Kot W = mg = ρtekoče. V. g, Moraš:

B = ρ_tekoče. V_potopljen. g

Ki je ravno izraz za potisk, omenjen v prejšnjem razdelku.

Načelne aplikacije Archimedes

Baloni, ki plavajo: načelo Archimedes v akciji

Načelo Archimeda se pojavlja v številnih praktičnih aplikacijah, med katerimi lahko poimenujemo:

- Aerostatski balon. Ki s povprečno gostoto manj kot pri okoliškem zraku plava v njem zaradi potisne sile.

- Ladje. Čelada ladij je težja od vode. Če pa trup šteje za zrak v notranjosti, je količnik med skupno maso in prostornino manjši od vode in to je razlog, zakaj ladje plavajo.

- Življenjski jopiči. Ko so zgrajeni iz svetlobnih in poroznih materialov, lahko plavajo, ker je razmerje med maso in volum.

- Plavajoči za zapiranje polnjenja posode za vodo. To je krogla, polna velikega volumna, ki plava nad vodo, kar povzroči potisno silo - pomnoženo z učinkom ročice - zapre pokrovček za polnjenje rezervoarja za vodo, ko doseže raven nivoja.

Lahko vam služi: enodimenzionalni valovi: matematični izraz in primeri

Primeri

Primer 1

Legenda pravi, da je kralj Hierón zlatim zlatim zlatim dal krono, toda nezaupljiv monarh je menil, da bi zlatar lahko varal, ko je v krono postavil manj dragoceno kovino kot krono. Toda kako bi lahko vedel, ne da bi uničil krono? 

Kralj je naročil Archimedes in to je iskal rešitev, odkril njegovo znano načelo.

Recimo, da krona tehta 2,10 kg-f v zraku in 1,95 kg-f, ko je popolnoma potopljena v vodo. V tem primeru ni prevare?

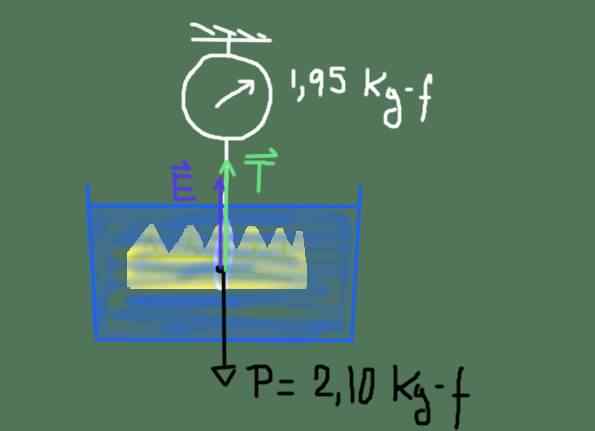Diagram telesa brez krone King Heron. Vir: Pripravil F. Zapata

Diagram sil je prikazan na prejšnji sliki. Te sile so: teža Str krone, potisk In in napetost T vrvi, ki visi iz lestvice.

P = 2,10 kg-f in t = 1,95 kg-f je znano, je treba določiti velikost potiska In:

T + e = p ⇒ e = p - t = (2.10 - 1,95) kg -f = 0,15 kg -f

Po drugi strani pa je po načelu Archimedes potis enakovreden teži izseljene vode prostora, ki jo zaseda krona, to je gostota vode zaradi volumna krone zaradi pospeška gravitacije :

E = ρ_voda⋅v⋅G = 1000 kg/m^3 ⋅ v ⋅ 9,8m/s^2 = 0,15 kg ⋅ 9,8 m/s^2

Kjer je mogoče izračunati volumen krone:

V = 0,15 kg / 1000 kg / m^3 = 0,00015 m^3

Gostota krone je količnik med maso krone iz vode in glasnostjo njene:

Gostota krone = 2,10 kg / 0,00015 m^3 = 14000 kg / m^3

Gostoto čistega zlata lahko določimo s podobnim postopkom, rezultat pa je 19300 kg/m^3.

Če primerjamo obe gostoti, je očitno, da krona ni čisto zlato! 

Primer 2 

Na podlagi podatkov in rezultata primera 1 je mogoče ugotoviti, koliko zlata je ukradel zlati zlati v primeru, da je del zlata nadomestil srebro, ki ima gostoto 10500 kg/m^3 3 3 3.

Poklicali bomo ρc na gostoto krone, ρo do gostote zlata in ρ_str do gostote srebra.

Skupna masa krone je:

M = ρc⋅v = ρo⋅vo + ρ_str⋅vp

Skupna količina krone je prostornina srebra in volumen zlata:

V = vo + vp ⇒ vp = v - VO

Zamenjava v masni enačbi:

ρc⋅v = ρo⋅vo + ρ_str⋅ (v - vo) ⇒ (ρo - ρ_str) Vo = (ρc - ρ_str) V

To pomeni, da je količina zlata, ki vsebuje krono celotnega volumna V,:

Vo = v⋅ (ρc - ρ_str)/(ρo - ρ_str) = ..

… = 0,00015 M^3 (14000 - 10500)/(19300 - 10500) = 0,0000596 M^3

Če poznamo težo v zlatu, ki vsebuje krono, pomnožimo VO za gostoto zlata:

Vam lahko služi: pravilo desnega roka

MO = 19300 *0.00005966 = 1,1514 kg

Ker je masa krone 2,10 kg, vemo, da je zlato ukradel 0,94858 kg zlata in nadomestil srebro.

Rešene vaje

Vaja 1

Ogromen helijev balon lahko vzdržuje v ravnovesju (ne da bi se dvignil ali se spustil) osebi.

Predpostavimo, da je teža osebe in košara, strune in balon 70 kg. Kakšna je količina helija, ki je potrebna za to? Kakšne velikosti bo imel balon?

Rešitev

Domnevali bomo, da potisk proizvaja predvsem volumen helija in da je potisk preostalih komponent zelo majhen v primerjavi s helijem, ki zaseda veliko več volumna.

V tem primeru bo potreben volumen helija, ki bo lahko zagotovil 70 kg + težo.

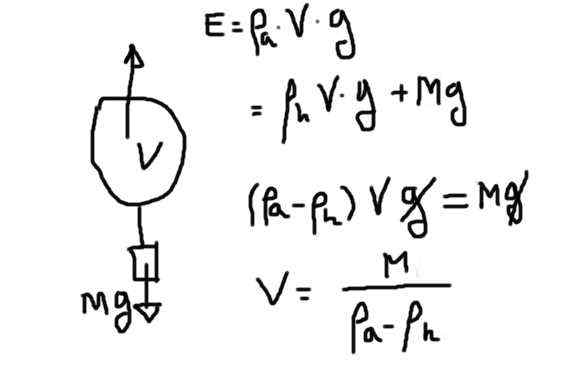Brezplačno telo fdiaogram, poln helija. Vir: Pripravil F. Zapata.

Potis je produkt volumna helija zaradi gostote helija zaradi pospeška gravitacije. Ta potisk mora kompenzirati težo helija in težo preostalih.

Da⋅v⋅g = da⋅v⋅g + m⋅G

kjer sklepa, da je v = m / (da - dh)

V = 70 kg / (1.25 - 0,18) kg/m^3 = 65.4 m^3

To pomeni, da je 65 potrebnih.4 m^3 helija pri atmosferskem tlaku za podporo.

Če predpostavimo, da sferični balon najdemo polmer istega iz razmerja med glasnostjo in polmerom krogle:

V = (4/3) ⋅π⋅r^3

Kjer je r = 2,49 m. Z drugimi besedami, potreben bo premer 5 m, poln helija.

Vaja 2

Materiali z nižjo gostoto, ki voda plavajo v istem. Predpostavimo, da imate polistirenske kocke (bela pluta), les in led. Njegove gostote v kg na kubični meter so: 20, 450 in 915.

Poiščite, kakšen del celotne prostornine je iz vode in kakšna višina izstopa glede na površino vode kot gostoto zadnjih 1000 kilogramov na kubični meter.

Rešitev 

Plavalnost se pojavi, ko je telesna teža zaradi vode enaka potiska:

E = m⋅G

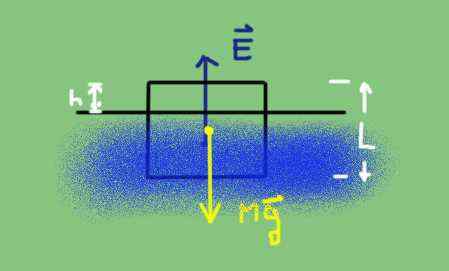Brezplačni karoserijski diagram delno potopljenega predmeta. Vir: Pripravil F. Zapata.

Teža je gostota telesa DC, pomnožena z volumnom V in pospeševanjem gravitacije G.

Potisk je teža razseljene tekočine v skladu z načelom Archimedes in se izračuna tako, da se pomnoži gostota D vode s potopljenim volumnom V 'in s pospeševanjem gravitacije.

To je:

D⋅v'⋅g = dc⋅v⋅g

Kar pomeni, da je potopljeni volumski delež enak količniku med gostoto telesa in gostoto vode.

(V '/v) = (dc/d) 

To pomeni, da je izjemna volumska frakcija (v "/v)

(V "/v) = 1 - (dc/d)

Ja h Je izjemna višina in L Kocka stran Volume frakcije lahko zapišemo kot

(H⋅l^2)/(l^3) = H/l, Z drugimi besedami, tudi izjemni višinski del je tudi

(h/l) = 1 - (dc/d)

Potem so rezultati za zahtevane materiale:

Polistiren (bela pluta):

(H/l) = (v "/v) = 1 - (dc/d) = 1- (20/1000) = 98% iz vode

Les:

(h/l) = (v "/v) = 1 - (dc/d) = 1- (450/1000) = 55% iz vode

Led:

(h/l) = (v "/v) = 1 - (dc/d) = 1- (915/1000) = 8.5% iz vode

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill. 417-455.
2. CENGEL Y, Cimbala J. 2011.Mehanika tekočine. Osnove in aplikacije. Prva izdaja. McGraw Hill.
3. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 4. Tekočine in termodinamika. Uredil Douglas Figueroa (USB). 1 - 42.
4. Giles, r. 2010. Tekočina in hidravlična mehanika. McGraw Hill. 
5. Rex, a. 2011. Osnove fizike. Pearson. 239-263.
6. Tippens, str. 2011. Fizika: pojmi in aplikacije. 7. izdaja. McGraw Hill.