Fizično

Relativna tlačna formula, kako se izračuna, primeri, vadba

Relativna tlačna formula, kako se izračuna, primeri, vadba

The Presirelativni Ón Je tisto, kar se meri glede na določeno vrednost oz Datum, ki je običajno atmosferski tlak na gladini morja (standardni atmosferski tlak). To je primerno, ker se velik del meritev tlaka izvaja pod plinastimi plastmi, ki predstavljajo atmosfero, ki ima svoj pritisk.

Po drugi strani se absolutni tlak meri glede na skupni vakuum, v katerem ni molekul, ki bi medsebojno vplivali. V posodi, v kateri je bil narejen vakuum, ni delcev, ki delujejo od notranjosti na stenah ali na predmetih v njem.

Slika 1. Za merjenje relativnega tlaka se uporablja tako merilnik tlaka. Vir: Wikimedia Commons.

Izmerjeni pritiski so lahko nad ali pod atmosferskim tlakom. V prvem primeru govori o Tlak merilnika In v drugem Vakuumski tlak.

Običajno so pritiski, ki se vsak dan merijo v pnevmatikah in krvnem tlaku, relativni pritiski, medtem ko se v atmosferskem tlaku meri z barometrom, je absolutni tlak.

[TOC]

Formula relativnega tlaka

Relativni tlak je razlika med absolutnim tlakom PAbs in atmosferski tlak pBankomat, Je diferencialni tlak ali razlika v tlakih. Pri relativnem tlaku pRel V angleščini je znano kot Tlak merilnika Strg In ga daje odnos:

StrAbs = PBankomat + Strg

StrRel = PAbs - StrBankomat

Za tlak se Pascal uporablja kot merilo mednarodnega sistema enot, ne glede na to, ali gre za absolutni tlak ali relativni tlak.

Pascal je enakovreden sili, ki jo ima 1 Newton na območju 1 m2, Vendar se pogosto uporabljajo druge enote, kot so živo srebro, voda, anglo -saksonske enote, kot so psi in drugi.

Vam lahko služi: 31 vrst sile v fiziki in njihove značilnosti

Kako se izračuna relativni tlak?

Če je absolutni tlak znan v eni točki in standardnem atmosferskem tlaku, je relativni tlak odštevanje med obema.

Recimo, da je absolutni tlak v določenem sistemu 305 kPa. Vedeti, da je standardni atmosferski tlak 101.3 kPa, relativni pritisk je:

Strg = PAbs - StrBankomat = 305 - 101.3 kPa = 203.7 kPa

KPA ali kilopascal je tisočkrat večji od Pascala. Uporablja se pogosteje, saj so vrednosti tlaka v vrstnem redu na tisoče Pascal. Teža jabolka je približno 1 Newton in pascional je enakovredna tej sili, razporejeni v 1 metrskem stranskem kvadratu. Drugi večkratniki, kot so Megapascal (1 MPa = 1 x 106 Pa) ali Gigapascal (1 gpa = 1x 109 Pa).

Tlak primera je manometričen, ker je nad atmosferskim pritiskom, vendar so pod tem absolutni pritiski. Na primer, če ima plin v posodi absolutni tlak 50 kPa, je njegov relativni tlak vakuumski tlak, ki proizvaja sesanje:

Strg = PAbs - StrBankomat = 50 - 101.3 kPa = -51.3 kPa

V teh primerih je bil uporabljen standardni atmosferski tlak, to je tlak na gladini morja. Če pa je pri izračunu potrebna večja natančnost, se lahko uporabi lokalni atmosferski tlak, ki se lahko razlikuje od 101.3 kPa, saj je odvisno od višine in drugih geografskih pogojev.

V besedilih so ponavadi navedeni pritiski sorazmerni in če je treba delati z absolutnimi pritiski, se ti razlikujejo z uporabo naročnin, da se izognejo zmedi.

Vam lahko služi: sonce

Sprememba tlaka z globino

Na vsaki točki znotraj tekočine, kot je voda, je tlak. Ob predpostavki, da je voda nestisljiva, zato njegova gostota ostane konstantna in tlak se razlikuje navpično.

Preverite ga lahko tako, da vzamete majhen del tekočine v obliki debelega diska Dy to je v mirovanju sredi tekoče mase.

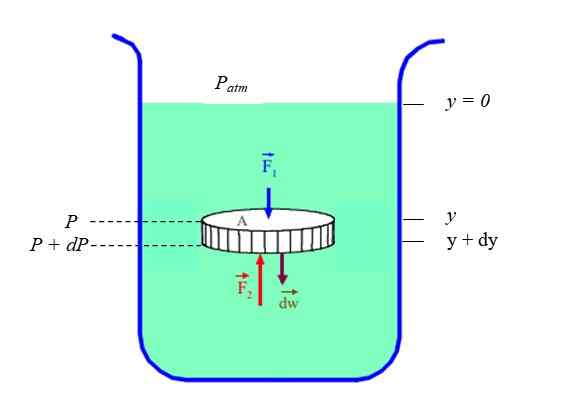Slika 2. Majhen del tekočine v obliki diska v statičnem ravnovesju. Vir: f. Zapata.

Sile na krožnih robovih diska prekličejo vrstniki, ne pa sile, ki jih izvaja masa tekočine nad in pod diskom: F1 in F2. Poleg tega je treba upoštevati težo tekočega diskaW V Newtonovem drugem zakonu:

∑fin = F2 - F1 - W = 0

Te sile se lahko izrazijo glede na tlak, ki je pravokotna sila na enoto območja. Na ta način imamo tlak P, ki ga proizvede sila F1:

F1 = P. Do

Kjer je a krožno območje diska. Podobno:

F2 = (P + DP). Do

S P + DP tlak na globini in + dy. Teža je dw = dm . G:

(P + DP). A - p. A - DM . G = 0

Gostota tekočine je ρ = dm/ dv, z DV volumna tekočega diska, ki jo daje a.Dy. Na ta način:

(P + DP). A - p. A - ρa.Dy .G = 0

Pridobljena enačba je poenostavljena na:

Dp - ρgdy = 0 → dp = ρgdy

Integracija obeh strani iz in1 do y2:

= P2 - Str1 = ρg (in2 - in1)

Izraz str2 - Str1 Je razlika v tlakih ali diferencialnem tlaku. Če želimo vedeti pritisk na navpični koordinatni točki in, to storimo in1 = 0, in2 = y in Strtudi = PBankomat. S tem bomo imeli pritisk glede na to globino, ki je odvisna izključno od globine in::

Vam lahko služi: nepravilna galaksija: tvorba, značilnosti, vrste, primeri

Str2 - StrBankomat = ρGy ⇒ PRel = ρy

Primeri relativnega tlaka

Pritisk na dnu bazena

Vsi smo doživeli pritisk, ki ga čutimo, če se potopimo v bazen ali v morju. Kakšen je relativni pritisk, ki ga čutimo s potopljenjem v bazen s sladko vodo na 5 metrov? Z uporabo prejšnjega izraza in vedenje, da je gostota sladke vode 1000 kg/m3, Z g = 9.81 m/s2 Relativni tlak je:

StrRel = ρGy = 1000 x 9.81 x 5 Pa = 49050 Pa.

Pritisk na pnevmatiko

Pnevmatike za vozila so običajno pri tlaku 32 psi. To je relativni ali manometrični tlak v kilogramih na kvadratni palec, enota, ki se uporablja v angleško govorečih državah. V teh enotah je kalibrirano veliko manometrov. 32 psi je enako 220632 Pa o 220 kPa.

Vaja rešena

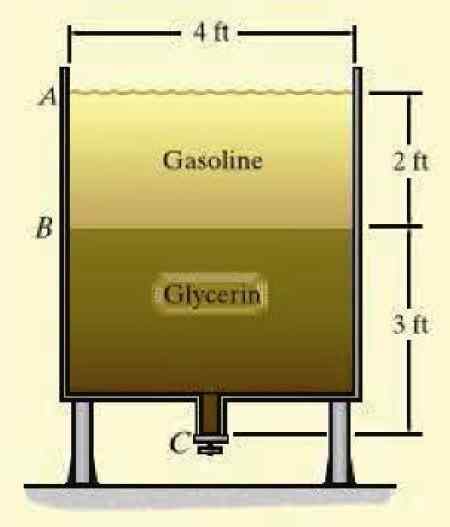
Rezervoar vsebuje bencin in glicerin, dve tekočini, ki niso misljivi (ne mešajte se) na navedenih višinah. Kakšen je manometrični tlak na dnu rezervoarja? Specifične uteži so pritrjene, označene z grško črko γ vsake tekočine:

γplin = 45.3 lb/ft3

γGly = 78.7 lb/ft3

Slika 3. Rezervoar, poln z dvema neizmernima tekočinama. Vir: Hibbeler, r. Mehanika tekočine.

Rešitev

Specifična teža γ tekočine je produkt njegove gostote zaradi pospeška gravitacije, zato se lahko enačba relativnega tlaka izrazi na naslednji način:

StrRel = γ.in

Relativni tlak na dnu rezervoarja je posledica teže stolpca glicerina in bencina in je neodvisen od oblike rezervoarja:

StrRel = γplin . inAb + γGly . inPr = (45.3 x 2 + 78.7 x 3) lb/ft2 = 326.7 lb/ft2

Reference

  1. Cimbala, c. 2006. Mehanika tekočin, osnov in aplikacij. MC. Graw Hill.
  2. Hibbeler, R. 2015. Mehanika tekočine. 1. Ed. Pearson.
  3. Mott, r.  2006. Mehanika tekočine. 4. Izdaja. Pearson Education.
  4. Sedi, a. 2006. Mehanika tekočine, fizični uvod. Alpha omega.
  5. Streeter, v. 1999. Mehanika tekočine. McGraw Hill.
  6. Zapata, f. Pritisk in globina. Okreval od: Francesfizike.Blogspot.com.