Kartezijansko letalo

Kaj je kartezijansko letalo?

On Kartezijansko letalo Sestavljen je iz para ravnih črt, pravokotnih drug na drugega in ki se v eni točki seka. Ena od črt je navpična in druga vodoravna, pri čemer se zavzema za točko križišča kot izvor sistema.

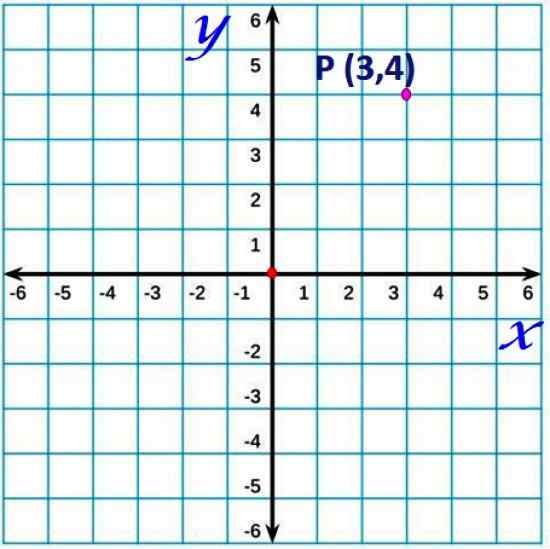
Cilj je enostavno najti katero koli ravno točko skozi par vrednosti: koordinat. Če želite to narediti, je na vsaki od vrstic zgrajena lestvica s celotnimi številkami, pozitivni so zapisani v eno smer, v drugi pa negativi, kot je prikazano na naslednji sliki:

Slika 1. Točka v kartezijanski ravnini. Vir: f. Zapata.

Po konvenciji se vodoravna os običajno imenuje x in navpična os kot os in.

Vsaka točka letala bo imela koordinate, ki jih določi urejen par (X, y). Na primer, točka P koordinate (3,4), ki se nahaja 3 enote desno od izvora in 4 enote navzgor, na zgornji sliki. Je podoben zemljevidu, ki označuje širino in dolžino določene lokacije.

Ker sta potrebni dve koordinati, je rečeno, da je letala dve dimenzionalni, vendar se koncept zlahka razširi na tri dimenzije, pri čemer dodamo bolj koordinatno os, ki je običajno označena kot z os z. V tem primeru se oblikujejo koordinate (X in z).

Kartezijansko letalo dobi ime francoski znanstvenik René Descartes (1596-1650), ki ga je formaliziral pri svojem delu Metoda govor iz leta 1637, čeprav je v delih Apolonija Perga (262-190 AC) zgodovina, matematik, ki je odkril stožčaste krivulje: obod, elipsa, parial in hiperbola.

Vam lahko služi: kocka razlika: formule, enačbe, primeri, vaje

Značilnosti kartezijanske ravnine

- Kot on Os x Kot Os y Na obeh koncih se raztezajo neskončno in sekajo pravokotno (pod kotom 90 stopinj). Ta funkcija se imenuje ortogonalnost.

- Točka, kjer se obe osi sekata, je znana kot izvor ali ničelna točka.

- Koordinatni sistem razdeli ravnino na štiri regije, imenovane kvadrante.

- Lokacije v koordinatni ravnini so opisane kot urejeni pari.

- Vsaka točka na kartezijanski ravnini je povezana z edinstveno koordinato X ter koordinato in edinstveno.

Elementi kartezijanske ravnine

Elementi kartezijanske ravnine so naslednji:

-The številčne črte tudi koordinirane osi x in y, Če je letalo. Os in Prejmite ime osi, medtem ko osi x To je os abscisa. Ko gre za prostor, se doda os z, sposoben predstavljati tako višino kot globino.

-On izvor, ki je točka presečišča osi.

-The kvadranti, ki so območja, ki jih koordinatne osi določajo na ravnini in se štejejo v nasprotni smeri do rok ure, začenši s prvim kvadrantom. So opredeljeni na naslednji način:

• Prvi kvadrant: osi x in in pozitivno.
• Drugi kvadrant: ustreza negativni osi x in pozitivni osi.
• Tretji kvadrant: ima obe negativni osi.
• Četrti kvadrant: s pozitivno osi x in in negativno osi.

Na splošno so kvadranti označeni v rimskih številkah, kot je ta:

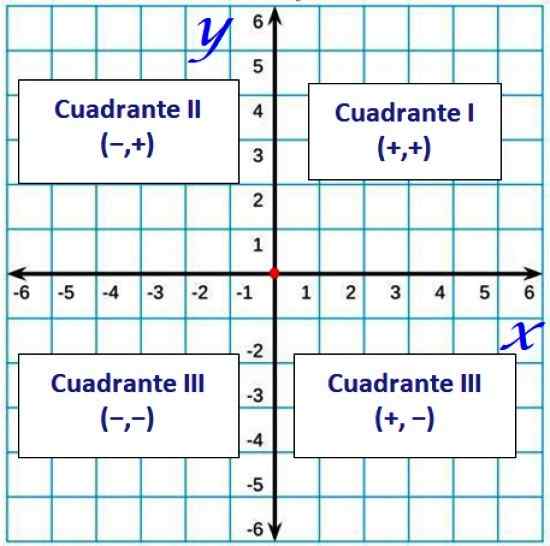Slika 2. Cuadranti v kartezijanski ravnini. Vir: f. Zapata.

Naročeni pari in razdalja med dvema točkama

Naročeni pari so koordinate vsake točke, v kateri je X koordinata vedno postavljena na prvo mesto, kot na primer slike 1. Koordinate (3,4) točke P kažejo, da to x = 3 in y = 4.

Na tej drugi sliki spodaj točka P spada v kvadrant IV in ima koordinate (2; −1.5). Upoštevajte, da s projiciranjem črte od koordinatnih osi do točke p tvori pravokotnik. To je razlog, zakaj se imenujejo tudi kartezijanske koordinate Pravokotne koordinate.

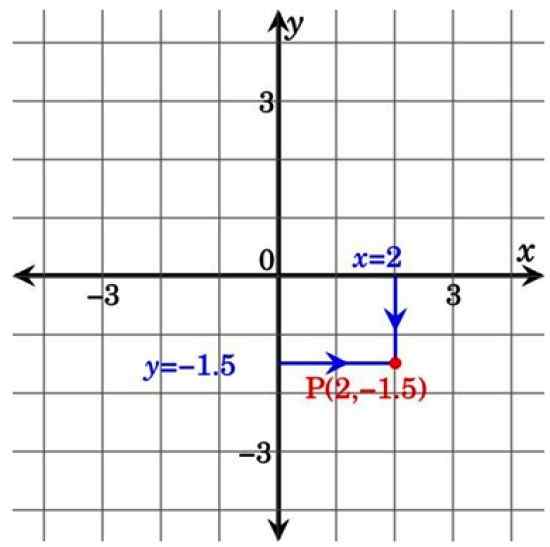Slika 3. Točka na kartezijanski ravnini. Vir: Wikimedia Commons.

Kartezijanske ravninske aplikacije

Kartezijanska letala ima veliko aplikacij na številnih področjih. Na začetku ga je Descartes v ravnini uvedel na grafične krivulje krivulj, zato velja za očeta analitične geometrije.

Vam lahko služi: Cruz izdelek

Vendar se njegova uporaba širi na grafiko vseh vrst odnosov in funkcij, kot so:

-Sledite usmeritvi telesa s paraboličnim, krožnim ali krivoarnim gibanjem na splošno.

-Grafično določite način, kako sta povezani dve spremenljivki s funkcijo.

-Poiščite točke na ravnem zemljišču, da jim olajšate meritve.

Reference

1. Matematika je zabavna. Kartezijanske koordinate. Okrevano od: matematika.com/podatki/kartezijanski koordinati.
2. Kartezijansko letalo. Pridobljeno iz: dl.UNCW.Edu.