Teža (fizični) Izračun, enote, primeri, vaje

On utež To je sila, s katero zemlja privabi predmete na svojo površino. Vsakič, ko se predmet spusti, gre na tla, ne more plezati po svojih sredstvi.

Vsi predmeti vedno privlačijo drug drugega, tudi malčke, le da je velikost sile, s katero počnejo, sorazmerna z maso. To pomeni, da predmeti z majhno maso imajo malo moči nad drugimi, vendar so nebesna telesa, kot je Zemlja, sposobna izvajati zelo veliko silo.

Zemlja ohranja luno okoli nje zaradi te sile privlačnosti, ki se imenuje Gravitacijska privlačnost Ko gre za predmete, ki so daleč od zemeljske površine, in utež Ko so predmeti blizu.

To sledi, da gravitacijska sila ne zahteva, da so predmeti nujno v stiku med seboj: zato se reče, da gre za silo na daljavo.

Predmeti imajo še vedno težo, tudi če so na določeni višini na tleh in bolj masivna, večja bo ta teža.

Veliki angleški znanstvenik Isaac Newton je prvi predstavil razlago o tem vprašanju z univerzalnim gravitacijskim zakonom, ki nosi njegovo ime, in od takrat služi, da razumejo, kako predmeti komunicirajo z maso z maso. To je zelo pomembno, saj ima vsak predmet na planetu težo.

[TOC]

Teža enote

Mednarodni sistem enot, če je teža za težo Newton, imenovan v čast Isaaca Newtona. To je enota za merjenje vseh vrst.

Newton, skrajšani N, je opredeljen kot potrebna sila za 1kg masni objekt za pridobitev pospeška 1m/s². Poleg Newtona obstajajo tudi druge enote sile skupne uporabe, na primer naslednje:

Kilogramska sila

On kilogramska sila o kilopondio, skrajšano KG-F ali KP, čeprav se običajno imenuje KG brez nadaljnjega. Potrebno je določiti lokacijo, saj, kot je navedeno, gravitacijsko polje doživlja variacije z višino in širino.

Ko nekdo reče, da tehta 45 kg, v resnici to pomeni, da je njihova teža 45 kg-f, ker je kilogram enota rezervirana za maso.

Vam lahko služi: odprto vezje

Enakovrednost med KG-F in N je: 1kg-f = 9.8 n

Funt

The Tehtnica-fuerza, Skrajšana LB-F je tudi enota sile, ki je analogna KG-F, saj je sila, ki jo zemlja izvaja na predmetu 1 lb mase. In tako kot pri KG-F ni težav z vrednostmi, ko ste na zemlji, to je predmet mase mase, tehta 1 lb-f-F.

Enakovrednost v LB-F in N je: 1 lb-f ≡ 4.44822 n.

Izračun teže in formula

Teža predmeta je sorazmerna z njegovo maso. Večja masa, večja teža.

Formula za iskanje obsega teže p (ali tudi W, kot včasih označuje "Utež" V angleščini) je zelo preprosto:

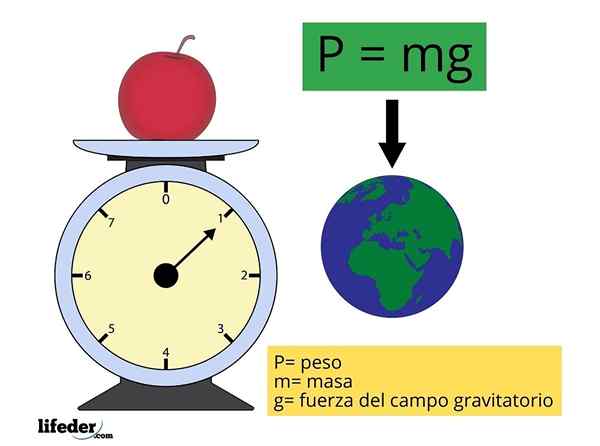
P = mg

Kje m predstavlja maso predmeta in g To je velikost pospeška gravitacije (intenzivnost gravitacijskega polja ali resnosti), približno konstantna in katerih vrednost je vzeta kot 9.81 m/s² Za najpogostejše izračune.

Teža je vektor in za razlikovanje med vektorjem in njegovo velikostjo se uporabljajo drzne črke. Na ta način se ob pogovoru o P razume, da gre za numerično vrednost in ko je napisano Str Sklicevanje je na vektor:

Str = m ∙g

The g S krepkimi besedili je to zemljiško gravitacijsko polje, to je vpliv, ki ga zemlja izvaja na prostoru, ki ga obdaja, ne glede na to, ali obstaja še eno telo, ki ga zaznava. Vsak predmet z maso ima svoje gravitacijsko polje, bodisi majhno ali veliko.

Intenzivnost gravitacijskega polja g Ni povsem stalen. Ima majhne različice, ki nastanejo predvsem zato, ker zemlja ni popolna sfera in tudi za lokalno višino in razlike v gostoti. Toda za večino aplikacij vrednost 9.81 m/s² Deluje zelo dobro.

Druga nebesna telesa imajo svoje značilno gravitacijsko polje, zato se pospešek gravitacije razlikuje glede na planet ali satelit. Isti predmet bi imel v vsakem drugačno težo, zato teža ni značilna lastnost stvari, ampak na temo na splošno.

Teža kot vektor

Teža je vektor in ima zato velikost, smer in pomen. V bližini zemeljske površine je teža navpični vektor in smer je vedno navzdol.

Na splošno je navpični naslov imenovan kot os in tudi z, In pomen je dodeljen znak + ali znak - da ga ločimo od smeri navzgor. Izbira je odvisna od lokacije izvora. Na spodnji sliki je bil izvor izbran na mestu, od koder pade jabolko:

Vam lahko služi: idealen plin: model, vedenje, primeri Teža je vektor, ki je usmerjen navpično navzdol. Vir: f. Zapata.

Vektor enote J, Za usmerjanje in razlikovanje navpične smeri se uporablja vektor, ki je enak 1, uporablja se. Glede tega vektorja je teža napisana tako:

Str = mg ( - J)

Kjer je negativni znak dodeljen smer.

Razlike med težo, maso in prostornino

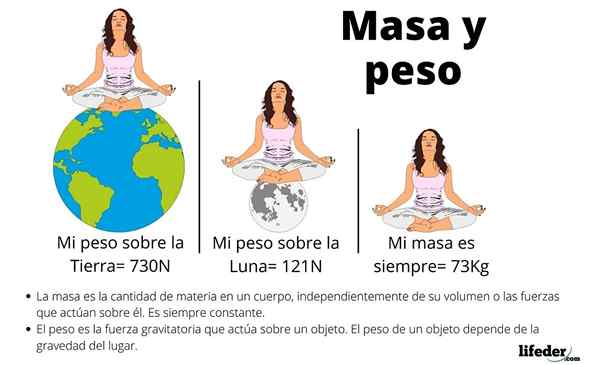
Pogosto so ti trije koncepti zmedeni, toda če pregledujemo značilnosti teže, jih je enostavno razlikovati od mase in volumna.

Za začetek je teža odvisna od gravitacijskega polja kraja, kjer je predmet. Na primer, na Zemlji in na Luni ima isto stvar drugačno težo, čeprav je količina atomov, ki jo sestavljajo.

Masa je skalarna velikost, povezana s količino atomov, ki sestavljajo objekt, in je dokazana z odpornostjo, da mora predmet spremeniti svoje gibanje, lastnost, imenovana Inercija.

Obseg je merilo prostora, ki ga zaseda predmet, še ena skalarna količina. Dva predmeta z enakim prostornino ne tehtata enako, na primer železna kocka tehta veliko več kot drug polistiren istih dimenzij.

V povzetku:

• Masa je povezana s količino snovi, ki jo ima telo.
• Teža je sila, ki jo zemlja izvaja na tej masi, sorazmerna.
• Prostornina je prostor, ki ga zaseda materija.

Treba je opozoriti, da sta skalarna količina, niti masa niti volumen nimajo smer ali pomena, ampak le številčna vrednost in ustrezna enota. Po drugi strani je treba težo, ki je vektor, vedno pravilno izraziti, kar kaže na velikost, enotnost, smer in pomen, kot v prejšnjem razdelku.

Primeri teže

Vsi predmeti na Zemlji imajo težo, lahko celo "tehtate" predmete, ki niso na zemlji, na primer drugi planeti ali sonce, čeprav je s posrednimi sredstvi seveda.

Ker je obseg teže zelo velik, se uporablja znanstveni zapis (v moči 10) za izražanje nekaterih, ki so zelo velike ali zelo majhne:

-Sonce: 1,989 × 10³⁰ kg-f

-Jupiter: 1,898 × ​​10²⁷ kg-f

-Komar: 2.0 × 10^-5 N

-Dojenčki: 34.3 n

-Otrok: 353 n

-Odrasla oseba: 65 kg-f

-Odrasli slon: 5.5 × 10³ kg-f

-Modri ​​kit: 1.0 × 10⁶ N

Vaja rešena

Škatla testa 20 kg počiva na mizi.

a) Poiščite težo škatle in normalno silo, ki jo na njem izvaja tabela.

Vam lahko služi: ohranjanje linearnega zagona: načelo, primeri, vaje.

b) Na prvi je nameščen še 10 kg škatle. Poiščite običajnega, ki ga tabela izvaja na 20 kg škatli in običajni, ki ga izvaja na najmanjši škatli.

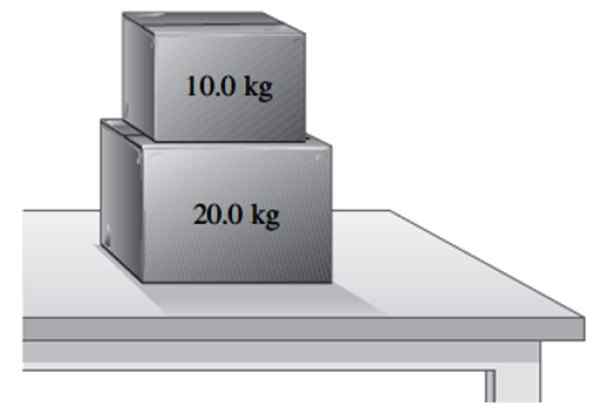Dve škatli, ki počivata na mizi. Vir: f. Zapata.

Rešitev

Na škatli je priročno narediti prosti shema telesa, ki je sestavljen iz risanja sil, ki delujejo nanj.

V tej situaciji je še vedno najmanjša škatla na vrhu, zato obstajata le dve sili: prva je teža Str ki je narisana navpično navzdol, kot je navedeno v prejšnjih razdelkih, in potem je tu normalno N, ki je pravokotna sila, ki jo izvaja tabela, in preprečuje, da bi škatla padla.

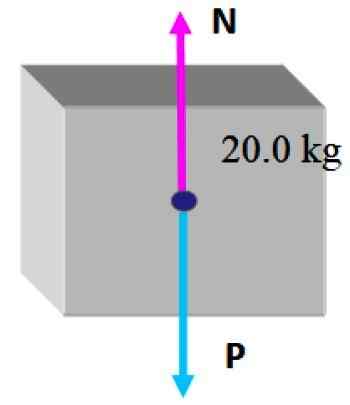
Ker je škatla v teh okoliščinah statično ravnovesje, je smiselno sklepati, da je velikost normalne enakomerne kot pri teži, tako da lahko nadomesti:

N = mg = 20.0 kg x 9.8 m/s² = 196 n; usmerjeno navpično navzgor.

Svoje delo je teža p = 196 n usmerjena navpično navzdol.

Rešitev b

Zdaj so narejeni novi brezplačni telesni diagrami o obeh predmetih. Za velike škatle se stvari nekoliko spremenijo, saj majhna škatla na njej izvaja moč.

Sile so naslednje: N in Str Oni so običajni, ki jih vadi miza in teža na škatli 20.0 kg, to se ni spremenilo. In nova sila, ki jo ima majhna škatla N₁, normalno zaradi stika z zgornjo stranjo velike škatle.

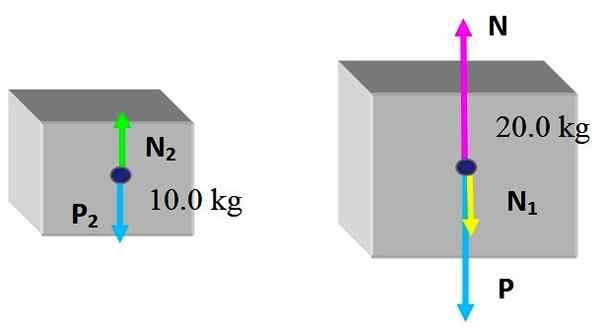
Kar zadeva majhno polje, prejme normalno N₂, ki ga izvaja zgornja obraz velike škatle in seveda njena teža Str₂. Ker so polja statično ravnovesje:

N₂ - Str₂ = 0

N - n₁ - P = 0

Od prve enačbe morate n₂ = P₂ = 10 kg x 9.8 m/s² = 98 n. Po zakonu o ukrepanju in reakciji je velikost sile, ki jo prejme majhna škatla, enaka, kot jo izvaja na veliki škatli, nato pa:

N₂ = N₁ = 98 n

Iz druge enačbe je normalno, da je tabela na velikem polju očiščena, kar ima na vrhu majhno škatlo:

N = n₁ + P = 98 n + 196 n = 294 n

Reference

1. Figueroa, d. 2005. Serija: Fizika za znanost in inženiring. Zvezek 2. Dinamično. Uredil Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fizika. 2. mesto. Ed. McGraw Hill.
3. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1. Pearson.
5. Serway, r., Jewett, J. 2008. Fizika za znanost in inženiring. Zvezek 1. 7. Ed. Cengage učenje.
6. Thomas Griffith, W. 2007. Konceptualna fizika. MC Graw Hill.