Y = 3sen (4x) delovno obdobje

On Y = 3sen (4x) delovno obdobje Je 2π/4 = π/2. Da bi jasno razumeli razlog za to izjavo, mora biti znana opredelitev obdobja funkcije in obdobje funkcije Sen (x); Koristno bo tudi malo o funkcijah.

Trigonometrične funkcije, kot sta sinus in kosinus (Sen (x) in cos (x)), so zelo koristne tako pri matematiki kot v inženirstvu.

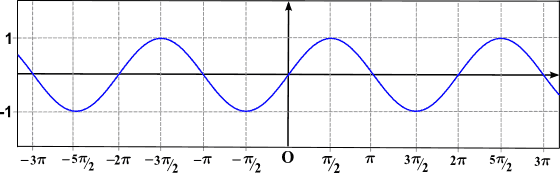
Besedno obdobje omenja ponavljanje dogodka, tako da rečemo, da je funkcija periodična, enakovredna pravi, da je "njen graf ponavljanje kosa krivulje". Kot je razvidno iz prejšnje slike, je funkcija sen (x) periodična.

Periodične funkcije

Funkcija F (x) naj bi bila periodična, če obstaja resnična vrednost p ≠ 0, tako da je f (x+p) = f (x) za vse x v domeni funkcije. V tem primeru je obdobje funkcije P.

Na splošno se imenuje obdobje funkcije pri najnižjem pozitivnem realnem številu P, ki izpolnjuje definicijo.

Kot je razvidno iz prejšnjega grafa, je funkcija Sen (x) periodična in njegovo obdobje je 2π (funkcija kosinusa je tudi periodična, obdobje pa je enako 2π).

Spremembe v grafu funkcije

Naj bo F (x) funkcija, katere graf je znan, in bo pozitivna konstanta. Kaj se zgodi z grafom f (x), če pomnoži f (x) s c? Z drugimi besedami, kakšen je graf C*F (x) in F (CX)?

C*f graf (x)

Z množenjem funkcije, zunaj s pozitivno konstanto, se graf F (x) spremeni v izhodnih vrednostih; To pomeni, da je sprememba navpično in dva primera je mogoče vzeti:

- Če je C> 1, potem graf trpi navpični raztežaj s C faktorjem.

- DA 0

F Graf (CX)

Kadar se argument funkcije pomnoži s konstanto, graf F (x) trpi spremembo vhodnih vrednosti; To pomeni, da je sprememba vodoravno in, tako kot prej, je mogoče vzeti dva primera:

- Če je C> 1, potem graf utrpi vodoravno stiskanje s faktorjem 1/c.

- DA 0

Y = 3sen (4x) delovno obdobje

Treba je opozoriti, da v funkciji f (x) = 3SE (4x) obstajata dve konstanti, ki spreminjata graf funkcije sinusa: ena množična zunanja in druga na notranji način.

3, ki je zunaj sinusne funkcije, je funkcija navpično razširiti s faktorjem 3. To pomeni, da bo graf funkcije 3SEN (x) med vrednostmi -3 in 3.

4, ki je znotraj sinusne funkcije, je funkcijski graf a horizontalno stiskanje za 1/4 faktorja.

Po drugi strani se obdobje funkcije meri vodoravno. Ker je obdobje funkcije Sen (x) 2π, se bo ob upoštevanju sin (4x) velikost obdobja spremenila.

Če želite vedeti, kakšno je obdobje y = 3sen (4x), samo pomnožite obdobje funkcije sen (x) z 1/4 (kompresijski faktor).

Z drugimi besedami, obdobje funkcije y = 3sen (4x) je 2π/4 = π/2, kot je razvidno iz zadnje grafike.