Obod kroga, kako ga izvleči in formule, rešene vaje

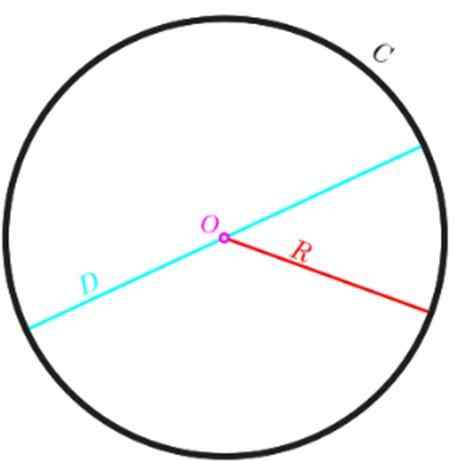
On obod kroga Je nabor točk, ki tvorijo konturo kroga in je znana tudi kot dolžina oboda. Odvisno je od polmera, saj bo večji obod očitno imel večjo konturo.

Biti Str Obod kroga in R polmer istega, potem lahko izračunamo Str Z naslednjo enačbo:

P = 2π.R

Obod kroga (v tem primeru pica) je odvisen od njegovega radia. Vir: Pixabay.

Kjer je π resnično število (bere "pi"), ki je vredna približno 3.1416… Sussing točke so posledica dejstva, da ima π neskončne decimalke. Zato je pri izračunih treba zaokrožiti svojo vrednost.

Vendar pa je za večino aplikacij dovolj, da vzamemo tukaj navedeni znesek, ali uporabite vse decimalke, ki jih kalkulator, s katerimi deluje.

Če je namesto polmera raje uporaba premera D, za katerega vemo, da je dvakrat večji polmer, je obod izražen na naslednji način:

P = π.2r = π.D

Ker je obod dolžina, ga je treba vedno izraziti v enotah, kot so števci, centimetri, stopala, centimetre in še več, odvisno od prednostnega sistema.

[TOC]

Obobov in krogi

Pogosto so izrazi, ki se uporabljajo zamenljivo, torej kot sinonimi. Vendar se zgodi, da med njimi obstajajo razlike.

Beseda "obod" izvira iz grškega "obdobja", kar pomeni konturo in "podzemno železnico" ali ukrep. Obseg je kontura ali obod kroga. Formalno je definirano:

Obseg je niz točk z enako razdaljo do točke, imenovane središče, ta razdalja je polmer oboda.

Krog je definiran na naslednji način:

Krog je niz točk, katerih razdalja do točke, imenovane center, je manjša ali enaka fiksni razdalji, imenovani radio.

Bralec lahko opozori subtilno razliko med obema konceptoma. Obseg se nanaša samo na niz robnih točk, krog pa je niz točk od roba do znotraj, od katerih je obod meja.

Vam lahko služi: vaje za čiščenje formule

Vaje dEmostracija izračuna oboda kroga

V naslednjih vajah bodo opisani koncepti izvedeni v praksi, pa tudi nekatere druge, ki bodo pojasnjeni, kot se pojavljajo. Začeli bomo od najpreprostejšega in stopnja težav se bo postopoma povečala.

- Vaja 1

Poiščite obod in območje 5 cm radijskega kroga.

Rešitev

Enačba, podana na začetku, se uporablja neposredno:

Str = 2π.R= 2π.5 cm = 10 π cm = 31.416 cm

Za izračun območja Do Uporablja se naslednja formula:

Do = π.R² = π. (5cm)²= 25π cm²= 78.534 cm²

- Vaja 2

a) Poiščite obod in območje praznega območja naslednje slike. Središče zasenčenega kroga je na rdeči točki, središče belega oboda.

b) Ponovite prejšnji razdelek za senčno regijo.

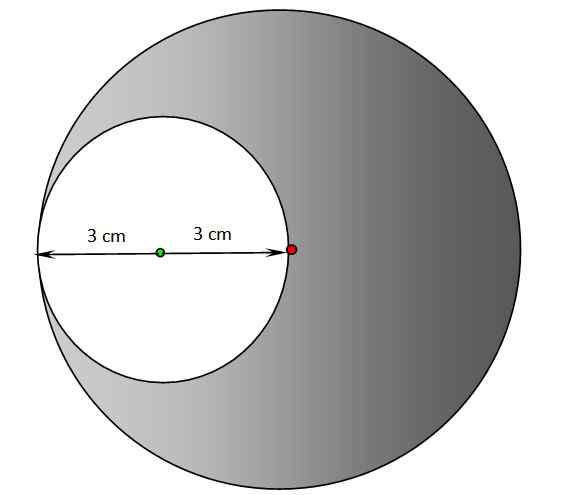Krogi za vajo 2. Vir: f. Zapata.

Rešitev

a) Polmer belega oboda je 3 cm, zato uporabljamo iste enačbe kot v vaji 1:

Str = 2π.R= 2π.3 cm = 6 π cm = 18.85 cm

Do = π.R² = π. (3cm)²= 9π cm²= 28.27 cm²

b) Za zasenčen krog je polmer 6 cm, njegov obod je dvakrat več kot v oddelku A):

Str = 2π.R= 2π.6 cm = 12 π cm = 37.70 cm

In končno se območje senčene regije izračuna na naslednji način:

- Najprej je območje zasenčenega kroga, kot da bi bilo popolno, ki ga bomo poklicali ", kot je to:

Do ' = π.R²= π.(6 cm)² = 36π cm²= 113.10 cm²

- Nato na območje Do ' Območje belega kroga se odšteje, predhodno izračunano v oddelku A), na ta način se zahteva zahtevano območje, ki bo označeno preprosto kot:

A = a ' - 28.27 cm² = 113.10-28.27 cm² = 84.83 cm²

- Vaja 3

Poiščite območje in obod zasenčenega območja na naslednji sliki:

Vam lahko služi: dodatni koti: kaj so, izračun, primeri, vaje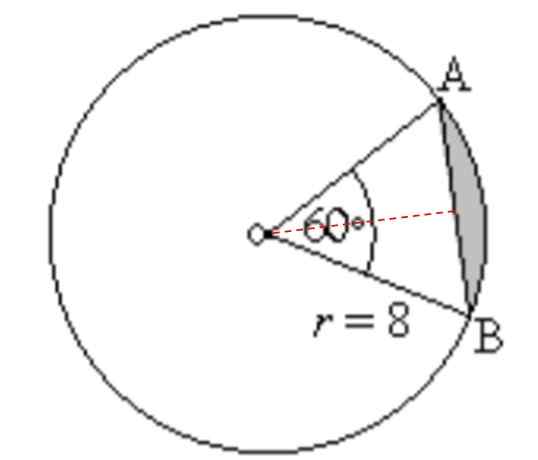Slika za vajo 3. Vir: f. Zapata.

Rešitev

Izračun območja zasenčene regije

Najprej izračunamo območje Krožni sektor ali klin, med ravnimi segmenti OA in OB ter krožnim AB segmentom, kot je prikazano na naslednji sliki:

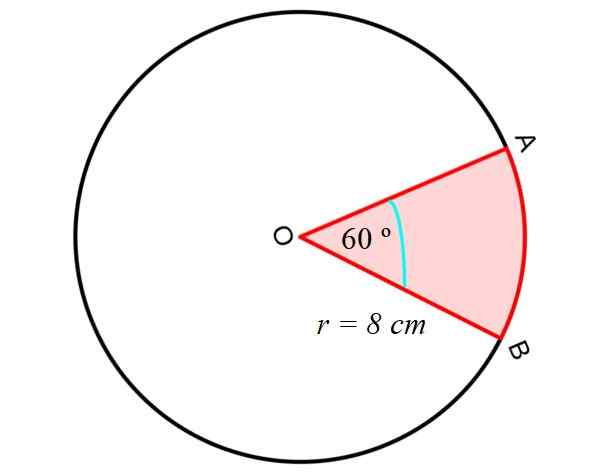
Za to se uporablja naslednja enačba, ki nam daje območje krožnega sektorja, ki poznamo polmer R in osrednji kot med segmentom OA in OB, torej dva radia oboda:

Do _{Krožni sektor} = Π.R². (αº/360 °)

Kjer je αº osrednji kot - je osrednji, ker je njena vrhova središče oboda - med dvema radioma.

1. korak: Izračun območja krožnega sektorja

Na ta način je območje sektorja, prikazanega na sliki,:

Do _{Krožni sektor} = Π.R². (αº/360 °) = π. (8 cm)². (60 °/360 °) = (64/6) π cm²= 33.51 cm²

2. korak: Izračun območja trikotnika

Nato bomo izračunali območje belega trikotnika na sliki 3. Ta trikotnik je enakostraničen in njegovo območje je:

Do _Trikotnik = (1/2) Osnovna višina x

Višina je pikčasta rdeča črta, prikazana na sliki 4. Če ga želite najti, lahko na primer uporabite teorem Pythagoras. Ampak to ni edini način.

Bralec opazovalca bo opazil, da je enakostranični trikotnik razdeljen na dva enaka pravokotnika, katerih osnova je 4 cm:

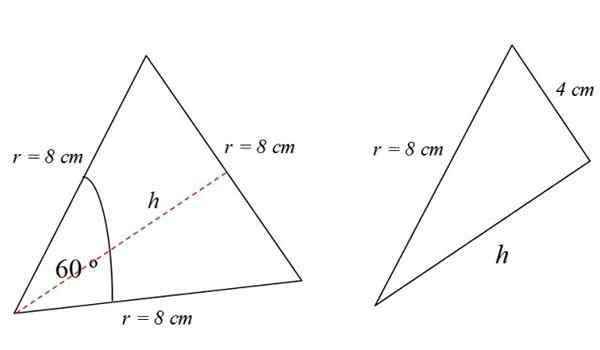
V desnem trikotniku je torej izpolnjen teorem pitagore:

Ker imate višino trikotnika, tako pravokotnik kot enakostranično, se izračuna njeno območje:

Do _Trikotnik = (1/2) Osnovna višina x = (1/2) 8 cm x 6.93 cm = 27.71 cm².

3. korak: Izračun zasenčenega območja

Dovolj je, da odštejemo glavno območje (krožni sektor) manjšega območja (enakostranični trikotnik): a _{zasenčena regija} = 33.51 cm² - 27.71 cm² = 5.80 cm².

Izračun oboda senčene regije

Iskani obod je vsota 8 cm pravokotne strani in AB obodnega loka.  Vendar pa celoten obod podvrže 360 ​​°, torej lok, ki je pod 60 ° šesti del celotne dolžine, za katerega vemo, da je 2.π.A:

Lahko vam služi: Graščanje funkcije: Kako jo prepoznati, primeri, vaje

Ab = 2.π.R / 6 = 2.π.8 cm / 6 = 8.38 cm

Zamenjava, obod zasenčenega območja je:

P = 8 cm + 8.38 cm = 16.38 cm.

Prijave

Obod je, tako kot območje, zelo pomemben koncept v geometriji in s številnimi aplikacijami v vsakdanjem življenju.

Umetniki, oblikovalci, arhitekti, inženirji in mnogi drugi ljudje izkoristijo obod, medtem ko razvijajo svoje delo, zlasti s krogom, saj je okrogla oblika povsod: od oglaševanja, do hrane do strojev.

Obod in krog sta med najbolj uporabljenimi geometrijami. Vir: Pixabay.

Če želite neposredno vedeti dolžino kroga, je dovolj, da ga zavijete z nitjo ali vrvico, nato pa to nit iztegnete in izmerite s trakom. Druga alternativa je merjenje polmera ali premera kroga in uporabe nekaterih zgoraj opisanih formul.

V vsakodnevnem delu se koncept oboda uporablja, ko:

-Ustrezen kalup je izbran za določeno velikost pice ali torte.

-Urbana cesta bo zasnovana z izračunom velikosti rekoma, kjer se avtomobili lahko spremenijo, da spremenijo pomen.

-Vemo, da se zemlja vrti okoli sonca v približno krožni orbiti -v resničnosti so planetarne orbite eliptične, po Keplerjevih zakonih -, vendar je obod zelo dober pristop k večini planetov.

-Izbran je ustrezna velikost obroča ali prstana, ki bo kupljen v spletni trgovini.

-Izberemo ključ do prave velikosti, da sprostimo matico.

In še veliko več.

https: // youtu.Biti/cr8xjryl5tk

Reference

1. Brezplačne matematične vadnice. Območje in obod kroga - kalkulator geometrije. Okrevano od: Analyzemath.com.
2. Open Reference Math Open. Obod, obod kroga. Okreval od: Mathpenref.com.
3. Inštitut Monterey. Obod in območje. Okreval od: montereyinstitute.org.
4. Znanstvenik. Kako najti obod kroga. Okrevano od: Znanstvenik.com.
5. Wikipedija. Obod. Pridobljeno iz: v.Wikipedija.org.