Naročen par

Kaj je urejen par?

Urejen par oz duet Gre. Omenjena merila določa, kateri od obeh elementov gre na prvo mesto in kateri gre.

Naročeni par je označen kot (x, y), kjer je "x" prvi element para, "Y" Komponente. Na splošno (x, y) ni isti urejen navor (y, x). In poleg vrstnega reda je še ena pomembna značilnost urejenih parov enakost: dva urejena para (a, b) in (c, d) sta enaka le, če sta a = c in b = d.

Slika 1.- Zahvaljujoč urejenim parom, mladič ve, da so kosti pokopane na lokacijah (3,1) in (-4,2), medtem ko je njegova hiša v (0,0). Vir: f. Zapata.

Primeri urejenih parov bi bili tisti, ki so sestavljeni iz starosti, in teža študentov matematike. Naročeni par (15, 62) ustreza 15 -letni študentu, ki se razlikuje od malo verjetnega para (62,15).

Koncept urejenega navora je zelo pomemben na različnih področjih matematike, kot so kartezijanska ravnina, frakcije, vektorji v ravnini, odnosi in funkcije. Pomemben vidik je, da njihovi elementi nimajo nujno številčnih, na primer, lahko jih naročite z:

• Državno mesto
• Ime priimka
• Žena mož

In številne druge kombinacije.

Primeri urejenih parov

Frakcije

Delež je predstavljen kot količnik dveh celih P/Q, na primer del ½, ki je enakovreden decimalni številki 0.5.

Vendar ta frakcija ni edina, ki predstavlja decimalno 0.5, tako tudi naslednje:

2/4; 3/6; (-2)/(-4); 20/40; (-1)/(-2)…

Na ta način je lahko kateri koli del predstavljen kot urejen par (p, q), kjer sta p in q celotna, P pa zasedeta položaj števca in Q. Obstaja pomembna omejitev in da mora biti Q (imenovalec) drugačen od 0, saj frakcije obrazca P/0 niso definirane.

Vam lahko služi: končni niz: lastnosti, primeri, rešene vaje

In še en pomemben pogoj je, da sta dva ulomka A/B in C/D enaka, dokler se izpolnjuje:

A ∙ d = b ∙ c

Funkcije in njegovi grafi

Funkcija je mogoče izraziti kot niz urejenih parov. Na primer, z grafikovanjem funkcije v kartezijanski ravnini je prvi element dodeljen položaj neodvisne spremenljivke, drugi pa je dodeljena odvisna spremenljivka. To je urejen par.

Za funkcijo y = f (x) lahko urejen navor izražamo kot [x, f (x)]]. Na primer, razmislite o začetnem nizu:

A = 1, 2, 3, 4

V tem nizu so prve komponente urejenega para v skladu s funkcijo y = x². Nabor drugih komponent je:

B = 1, 4, 9, 16

In urejeni pari se oblikujejo:

(1,1); (2,4); (3, 9); (4; 16)

Spoštovanje.

Vektorji v ravnini

Vektorji so lahko v kartezijanski ravnini predstavljeni z urejenimi pari, kjer prvi element predstavlja vodoravno komponento "x", drugo pa navpično komponento "y". Za razlikovanje vektorjev od točk v ravnini jih označujemo s krepkimi črkami in kvadratni oklepaji se uporabljajo namesto oklepajev, kot je ta:

v =

Na primer vektor v = ima vodoravno komponento, ki je enaka 4 in navpične komponente, enaka 7. Njegov graf je:

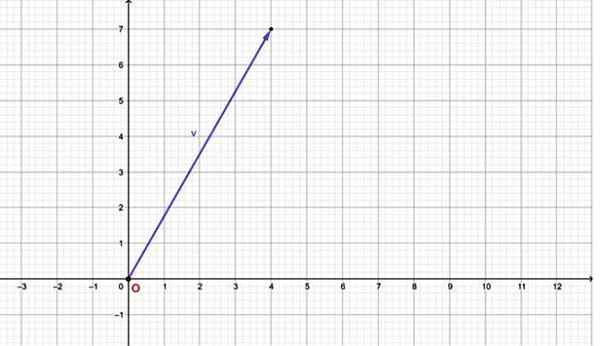Slika 2.- Ravninski vektor je mogoče izraziti z urejenim parom. Vir: f. Zapata.

Upoštevajte, da ima ta vektor svoj izvor sovpada z izvorom koordinatnega sistema (0,0). Če ima vektor svoj izvor na kateri koli drugi točki, ga je mogoče izraziti tudi v obliki urejenega navora skozi urejene pare.

Vam lahko služi: hierarhija operacij

Urejene operacije Pares

Dodatek

Naj bodo cilje (a, b) in (c, d) pari (d). Nov navor dobimo s pomočjo vsote v skladu z:

(a, b)+(c, d) = (a+c, b+d)

Nevtralni element

Nevtralni element dodajanja urejenih parov je navor (0,0), saj je vsota, ko doda urejeni par (A, B), slednja:

(a, b) + (0,0) = (a, b)

Vsota nasprotnega

Z dodajanjem urejenega para (a, b) s svojim nasprotnim (-a, -b) urejen navor (0,0):

(a, b) + (-a, -b) = (0,0)

Kommutativnost

Vrstni red dodatkov ne spremeni vsote:

(a, b) + (c, d) = (c, d) + (a, b)

Asociativnost

Rezultat dodajanja treh urejenih parov ni spremenjen, če je združen za izvajanje operacije:

[(a, b) + (c, d)] + (e, f) = (a, b) + [(c, d) + (e, f)]

Odštevanje urejenih parov

Naj bodo cilje (a, b) in (c, d), odštevanje se izvaja na naslednji način:

(A, B)-(C, D) = (A-C, B-D)

Izdelek

V izdelku obstajata dve možnosti: i) Pomnožite navor, ki ga naročite konstanta in ii) pomnožite dve (ali več) prašniki.

Množenje s konstanto

Naj bo K konstanta in urejen navor (a, b), izdelek med konstanto in navorom je:

K ∙ (a, b) = (k ∙ a, k ∙ b)

Množenje urejenih parov

Izdelek med urejenimi pari (a, b) in (c, d) se izvaja na naslednji način:

(A, B) X (C, D) = (AC - BD, BC+AD)

Nevtralni element

Nevtralni element množenja je (1.0), saj z množenjem vsakega navora, ki ga je to naročil, po zgoraj opisanem pravilu množenja, je prvotni navor:

(a, b) x (1.0) = (a - 0, b + 0) = (a, b)

Vam lahko služi: multiplikativno inverzno: razlaga, primeri, rešene vaje

Asociativnost

Ker vrstni red dejavnikov ne spremeni izdelka, ga je mogoče razvrstiti na različne načine, da pomnoži tri ali več urejenih parov in rezultat je enak:

[(a, b) x (c, d)] x (e, f) = (a, b) x [(c, d) x (e, f)]

Rešene vaje

Vaja 1

Ste naročili pare (x², X-2) = (16, 2). Kar je vrednost x?

Rešitev

Uporaba enakosti urejenih parov je najprej pridobina:

x² = 16 ⇒ x₁ = 4, x₂ = -4

Če želite vedeti, katera od obeh vrednosti izbere, uporaba:

X-2 = 2

x = 2 + 2 = 4

Zato je zahtevana vrednost x 4.

Vaja 2

Izrazite kot urejeno povežite vektor, ki sega od točke (1, 3) do točke (7, 11) in ga grafično predstavlja.

Rešitev

Biti v Vektor je iskal. Za določitev urejenega para, ki ga predstavlja in ki vsebuje njegove koordinate, se v tem vrstnem redu odštejejo koordinate prihoda in točke izvora. Tako:

v = =

Vektor je nato predstavljen v kot tisti, ki gre od (1,3) do (7, 11) in opreme v katerega izvor je pritrjen na izvor koordinatnega sistema (0,0). Kot vidite, imajo isto smer in pomen.

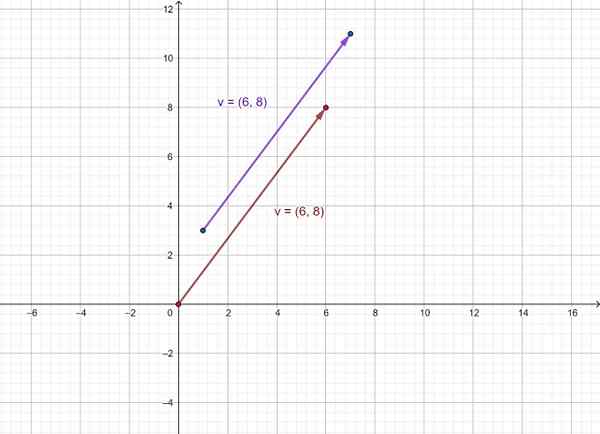Slika 3. Predstavitev vektorja kot urejen par. Vir: f. Zapata.

Reference

1. Poglobljeno. Naročen par. Okreval od: Deepai.org.
2. Matematika. Kartezijanski predstavitev vektorja s strani urejenega para. Okreval od: matemovil.com.
3. Varsity tutorrs. Naročen par. Pridobljeno iz: WarsityTorm.com
4. Priestri, Juan. Odnosi in funkcije. Fakulteta za strojništvo. Oddelek za matematiko. Univerza Buenos Aires. Pridobljeno od: Predmeti.fi.Uba.ar.
5. Univerza v Denverju. Odnosi. Okrevano od: matematika.Ucdenver.Edu.