Tri -dimenzionalni koncept, vrste in primeri

So Tri -dimenzionalni valovi Tiste, ki se širijo v vesolju, na primer zvočni val, ki ga ustvari zvočnik. Ta val se širi v vse smeri, čeprav ne z enako intenzivnostjo v vseh.

Če se v eni točki v vesolju pojavi motnja, se širi v treh prostorskih smereh, sprednje valovne fronte so zaprte, sferične, eliptične ali kakšne druge vrste.

Trijedimenzionalni valovi, ki jih proizvede govornik

Po drugi strani pa, če kraj, kjer izvirajo valovi.

[TOC]

Vrste treh dimenzionalnih valov

V treh dimenzionalnih valovih so valovne fronte niz površin, potopljenih v tridimenzionalni prostor.

Zdaj je valovna spredaj geometrijsko mesto vesoljskih točk, ki jih dosežemo z začetno motnjo, hkrati.

Tri vrste valov, ki potujejo v tridimenzionalnem prostoru, se običajno upoštevajo v skladu s simetrijo valovne sprednje: ravne valove, valjasti valovi in ​​sferični valovi. Vendar resnični valovi ne spadajo vedno v te vrste, ker nimajo tako visoke stopnje simetrije.

Ravni valovi

Ravni val, ki potuje v pozitivno smer X hitro V, je funkcionalno predstavljen kot:

G (x, t) = f (x - v⋅t)

Ta val ni omejen na osi x, pa tudi v naslovih in in z. Toda funkcionalna oblika kaže, da imajo vse točke, ki imajo isto koordinato X, ne glede na koordinate (z, y), enako vrednost G.

V tem primeru so valovne fronte ravnine vzporedne z z-in ravnino, ki hitro napredujejo v, kar pomeni, da ploski val zaseda ves tri dimenzionalni prostor.

Izraz, ki predstavlja raven val, ki se širi v katero koli smer ali hitro v, kje ali Predstavlja enote starejše direktorje vektorjev cos (α), cos (β) in cos (γ), je:

Vam lahko služi: reakcija entalpija: definicija, termokemija, vaje

g = f (û • r - v⋅t) = f (x cos (α) + in cos (β) + z cos (γ) - v⋅t)

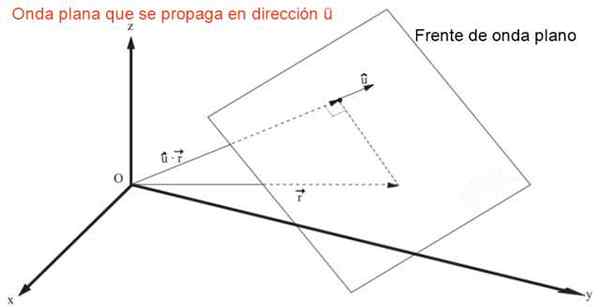Ravna valovna fronta, ki se hitro širi v tridimenzionalnem prostoru v. Vir: f. Zapata.

Z neposredno nadomeščanjem je enostavno dokazati, da je prejšnji izraz rešitev tridimenzionalne valovne enačbe, enačbe v delnih derivatih drugega linearnega reda:

∂_XxG + ∂_YyG + ∂_ZzG = (1/v²) ∂_Ttg

Prejsko enačbo lahko pišemo bolj kompaktno z uporabo laplacijskega operaterja ∇²:

∇²G = (1/v²) ∂_Ttg

Cilindrični valovi

Ko se začetna motnja porazdeli po ravni črti, se val širi v radialni smeri, pravokotno na to črto, ki napolni tridimenzionalni prostor, ki ga obdaja, z valjastimi valovnimi sprednjih frontah.

Sferični valovi

Ko je vir natančen in je medij, v katerem se razmnožuje tridimenzionalni val.

V primeru sferičnega vala, v katerem je intenzivnost vala v vseh smereh enaka, je funkcija, ki opisuje motnjo, odvisna le od razdalje r do pravočasnega in časovnega vira t.

V tem primeru je ustrezni LaPlacian:

∇²G = (1/r²) ∂_r(r² ∂_rG)

Je enačba valov:

∇²G = (1/v²) ∂_Ttg

Splošna rešitev bi bila:

g (r, t) = (1/r) f (r - v⋅t) + (1/r) g (r + v⋅t)

V tem primeru se reče, da gre za sferični val. Lahko pa obstajajo različice, kot bomo videli spodaj

Neizotropni sferični valovi

Zgodi se lahko tudi, da je sferični val, to je z valovnimi sprednjih sprednjicami, ki jih tvorijo koncentrične krogle do osrednje točke, amplituda ali intenzivnost vala v različnih smereh različna.

To se zgodi, ko je osrednji vir vala učinkovitejši v smeri kot drugi. 

Lahko vam služi: fizika pred Grki (Antigua Grčija)

Na primer, zvok, ki ga ustvari rog.

Intenzivnost ni enaka, čeprav signal traja isto čas, da doseže te točke. To je sferični val, ki ima nesferični usmerjevalni vzorec. 

Obstajajo tudi sferični valovi v primeru elektromagnetnih valov, ki jih ustvari antena, vendar v vseh smereh morda niso enako intenzivni.

Antena oddajnika

Ne -homogena polovica

Kadar medij ni homogen, je hitrost širjenja vala v različnih smereh drugačna.

Primer ne -homogenega medija je atmosfera, v kateri obstajajo razlike v tlaku z višino in obstajajo temperaturni gradienti. Drug primer so sloji Zemljine skorje, ki se razlikujejo po gostoti in elastičnem modulu. 

Ne-homogenost rezultat, da valovne fronte, ki izvirajo iz osrednjega natančnega vira.

Potem je tu tridimenzionalni val, katerega valovni spredaj ni sferičen.

Intenzivnost in energija sferičnega vala

Takšen lahko napišemo izraz sferičnega harmonskega vala:

g (r, t) = (g_tudi / r) cos (k⋅r - ω⋅t)

Kjer se valovne fronte širijo hitro enake:

V = ω/k

Njegova amplituda pa se zmanjšuje z obratno razdaljo r natančnega vira sferičnih valov.

Harmonični valovi imajo Gostota energije (Energija na enoto prostornine) ε dobiti od:

ε = ½ ρ Ω² (g_tudi / R)²

V tej enačbi:

-ρ Ima enote mase na enoto volumna in predstavlja gostoto medija, kjer se razmnožuje zvočni val.

-g_tudi To je amplituda premika elementa medija, na primer tekočina zaradi širjenja.

Vam lahko služi: viskozno trenje (sila): koeficient in primeri

Treba je opozoriti, da se, ker gre za sferični val, gostota energije zmanjšuje z obratnim kvadratom razdalje.

Intenzivnost vala, to je energija, ki se prenaša na enoto časa, je:

I = v⋅ε

Kot vedno je v praksi najpomembnejša velikost moč, ki se na enoto prenaša na radialno razdaljo r:

P = v⋅ε = i_tudi / r²

Biti Yo_tudi = ½ ρ v Ω² g_tudi².

Skupna energija, ki se prenaša na enoto časa s polmerom R, je:  P⋅4πr²= 4π⋅i_tudi, In kot je bilo pričakovano, ni odvisno od radialne razdalje. 

Primeri treh dimenzionalnih valov

Tri -dimenzionalni valovi so zelo pogosti, zato imamo:

Antene elektromagnetne valov

Valovi, ki jih proizvaja antena ali zvok, ki ga proizvaja prstna plošča, so trije dimenzionalni valovi, čeprav različnih narave

Zajemajo zelo širok spekter, od radijskih valov med stotinami kHz in sto MHz, do valov, ki jih oddaja antena antene Wifi vrstnega reda GHZ, ki že pade v obseg mikrovalovnih pečic. 

Vemo, da mikrovalovna pečica, čeprav niso ionizirajoče sevanje, lahko zvišajo temperaturo organizma, ker vsebuje veliko vode.

Zato ni priporočljivo imeti antene Wi-Fi blizu glave ali telesa. Samo malo se zberite, saj je na dvojni razdalji intenzivnost četrtina.

Potresni valovi

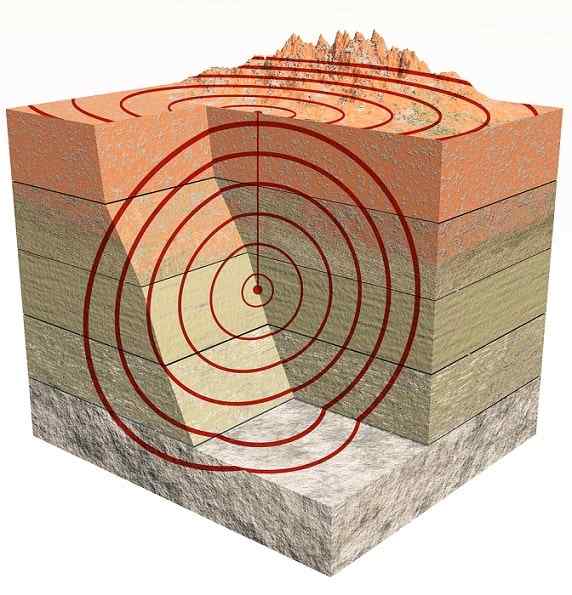Potresni valovi

So tudi trije dimenzionalni valovi. V glavnem obstajajo tipi Str ki so kompresijski valovi in ​​vrste S Kaj je rezanje ali striženjeSliši v angleščini).

Valovi Str ali primarni so prvi, ki so prišli, ker se širijo hitreje kot valovi S ali sekundarno.

Zvok

Zvok z govorom

Zvok je tridimenzionalni val. Ti valovi se širijo v vse smeri, čeprav, kot smo že rekli, ne z enako intenzivnostjo v vse smeri.

To je zato, ker vir zvoka ne oddaja vedno s popolnoma sferično simetrijo.

Reference

1. Baranek, l. 1969. Akustika. 2. mesto. Izdaja. McGraw Hill.
2. Griffiths g. Linearni in nelinearni valovi. Okreval od: Scholarpedia.org.
3. Nottoli, h. 2004. Fizika, ki se uporablja za arhitekturo. Nobuko.
4. Whitham g.B. 1999. Linearni in nelinearni valovi. Wiley. 
5. Wikivav. Nelinearni valovi. Okrevano od: wikivav.org