Transcendentne številke, ki so, formule, primeri, vaje

The transcendentne številke To so tisti, ki jih ni mogoče dobiti kot posledica polinomne enačbe. Nasprotno od transcendentne številke je a algebrska številka, ki so rešitve polinomne enačbe tipa:

do_n xⁿ + do_N-1 x^N-1 +… + A₂ x² + do₁ x + a₀ = 0

Kjer koeficienti_n, do_N-1,… Do₂, do₁, do₀ So racionalne številke, imenovane Polinomni koeficienti. Če je številka x rešitev prejšnje enačbe, potem ta številka ni transcendentna.

Slika 1. Dve številki velikega pomena v znanosti sta transcendentna številka. Vir: Javne domene.mreža.

Analizirali bomo nekaj številk in videli, ali so transcendentne ali ne:

a) 3 ni transcendenten, ker je rešitev x - 3 = 0.

b) -2 ne more biti transcendentni, ker gre za rešitev x + 2 = 0.

c) ⅓ je 3x - 1 = 0 rešitev

d) Raztopina enačbe x² - 2x + 1 = 0 je √2 -1, tako omenjena številka po definiciji ni transcendentna.

e) niti ni √2, ker je rezultat enačbe x² - 2 = 0. Z dvigom √2 kvadrata ima za posledico 2, kar odšteje od 2. Torej √2 je iracionalno število, vendar ni transcendentno.

[TOC]

Kaj so transcendentne številke?

Težava je v tem, da ni nobenega splošnega pravila za njihovo pridobitev (kasneje bomo rekli obrazec), vendar so nekatere najbolj znane številke pi in Številka Neper, označeno z: π in in.

Številka π

Število π Seveda se zdi, da opazuje, da matematični količnik med obodom P kroga in njegovega premera D, ne glede na to, ali je majhen ali velik krog, vedno daje isto število, imenovano pi:

π = P/D ≈ 3.14159…

To pomeni, da če se premer oboda jemlje kot merilna enota, bo za vse, bodisi velike ali majhne, ​​obod vedno vreden p = 3,14… = π, Kot je razvidno iz animacije slike 2.

Vam lahko služi: teorem Bolzano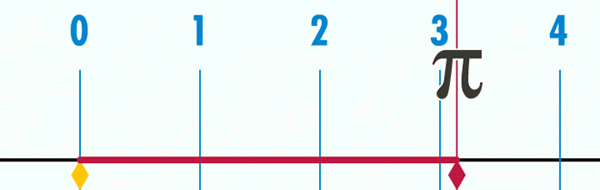Slika 2. Dolžina oboda kroga je včasih dolžina premera, približno 3.1416.

Če želite določiti več decimalk, morate izmeriti več natančnosti P in D in nato izračunati količnik, ki je bil narejen na matematičen način. Zaključek je, da decimali količnika nimajo konca in se nikoli ne ponavljajo, zato številka π Poleg tega, da je transcendenten, je tudi iracionalno.

Iracionalna številka je tista številka, ki je ni mogoče izraziti kot delitev dveh celotnih številk. 

Znano je, da je vsaka transcendentna številka neracionalna, vendar ni res, da so vsi iracionalni transcendentni. Na primer √2 je neracionalen, vendar ni transcendentna.

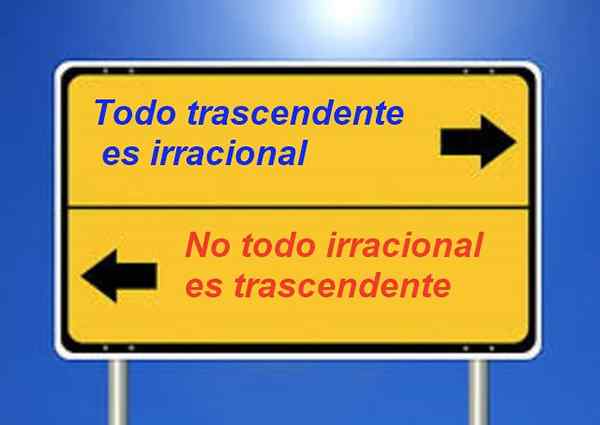Slika 3. Transcendentne številke so neracionalne, vendar vzajemna izjava ni resnična.

Številka e

Transcendentna številka je osnova neperijskih logaritmov in njihov decimalni pristop je:

E ≈ 2.718281828459045235360… .

Če ste želeli napisati številko in Točno bi bilo treba pisati decimalno neskončno, ker je vsaka transcendentna številka iracionalna, kot rečeno.

Prvih deset števk in Lahko si jih zapomnimo:

2.7 1828 1828 in čeprav se zdi, da sledi ponavljajočemu se vzorci.

Bolj formalna definicija in je naslednje:

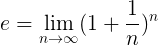
Kar pomeni, da je natančna vrednost in Operacija, navedena v tej formuli, je dosežena, ko je naravno število n Se nagiba k neskončnosti.

To pojasnjuje, zakaj lahko dobimo le pristope do in, Ker je velika številka n nameščena, lahko vedno najdete a n starejši.

Poiščite nekaj pristopov sami:

-Ko je n = 100 potem (1 + 1/100)¹⁰⁰ = 2.70481, ki komaj sovpada v prvi decimali z "resnično" vrednostjo E.

-Če ste izbrani n = 10.000 imate (1 + 1/10.000)^10.000 = 2.71815, ki sovpada z "natančno" vrednostjo E v prvih treh decimalih.

Vam lahko služi: homologne strani

Ta postopek je treba upoštevati, da lahko pridobimo "resnično" vrednost e. Mislim, da nimamo časa, da bi to dosegli, ampak poskusimo še en poskus:

Uporabimo n = 100.000:

(1 + 1/100.000)^100.000 = 2.7182682372

Da ima le štiri decimalke, ki sovpadajo z natančno vrednostjo.

Pomembno je razumeti, da večja je vrednost N, izbrana za izračun in_n, bližje bo resnične vrednosti. Toda ta resnična vrednost bo zadržana šele, ko je n neskončno.

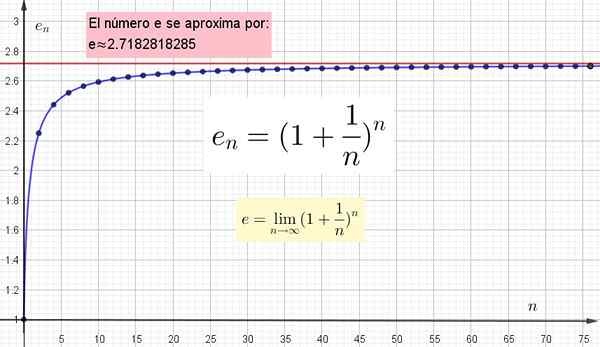Slika 4. Grafično je prikazan, saj je višja vrednost n bližje E, vendar mora biti doseganje natančne vrednosti n neskončno.

Druge transcendentne številke

Poleg teh znanih številk obstajajo tudi druge transcendentne številke, na primer:

- 2^√2

Vsaka algebrska številka, ki ni 0 ali 1, bo povišana na iracionalno eksponent, bo transcendentna številka.

-Champernownejeva številka 10: 

C_10 = 0,1234567891011112131415161718192021… .

-Številka Champernowne na bazi 2:

C_2 = 0,110111001011011… .

-Γ ali konstantno gama število Euler-Mascheroni:

γ ≈ 0,577 215 664 901 532 860 606

To dobimo z naslednjim izračunom:

γ ≈ 1 + ½ + ⅓ + ¼ +… + 1/n - ln (n)

Kdaj n biti zelo velik. Da bi imeli natančno vrednost gama številke, bi bilo treba izračunati z n neskončno. Nekaj ​​podobnega tistemu, kar smo storili zgoraj.

In obstaja veliko več transcendentnih številk. Veliki matematik Georg Cantor, rojen v Rusiji in je živel med letoma 1845 in 1918.

Formule, kjer se pojavi transcendentna številka π

Obod oboda

P = π d = 2 π r, kjer je p obod, d premer in r polmer oboda. Ne pozabite, da:

Vam lahko služi: koliko morate dodati 3/4, da dobite 6/7?

-Premer oboda je najdaljši segment, ki se pridruži dvema točkama in ki vedno prehaja skozi njeno središče,

-Polmer je polovica premera in je segment, ki sega od središča do roba.

Območje kroga

A = π r² = ¼ π d²

Površina krogle

S = 4 π r^2.

Ja. Čeprav se ne zdi, je površina krogle enaka kot v štirih krogih istega polmera kot krogla.

Prostornina krogle

V = 4/3 π r³

Vaje

- Vaja 1

"Eksotična" picerija prodaja tri premera pizz: 30 cm majhne, ​​srednje 37 cm in velikih 45 cm. Otrok je zelo lačen in je spoznal, da imata dve majhni pizzi enake stroške kot velike. Kaj bo boljše zanj, kupite dve majhni pizzi ali veliko?

Slika 5.- Območje pice je sorazmerno s kvadratom polmera, ki je sorazmerna konstanta. Vir: Pixabay.

Rešitev

Večja kot je območje, večja je količina pice, zato bo površina velike pice izračunana in primerjana s površino dveh majhnih pizz:

Veliko območje pice = ¼ π d² = ¼ ⋅3,1416⋅45² = 1590,44 cm²

Majhno območje pice = ¼ π d² = ¼ ⋅3,1416⋅30² = 706,86 cm²

Zato bosta imela dve majhni pizzi območje 

2 x 706,86 = 1413,72 cm² .

Jasno je: več pice bo kupilo eno veliko od dveh malčkov.

- Vaja 2

"Eksotična" picerija prodaja tudi 30 cm polmer polume -man -pizza za isto pravokotno obliko 30 x 40 cm strani. Kateri bi izbrali?

Slika 6.- Površina pol -zvočnika je dvakrat večja od krožne površine osnove. Vir: f. Zapata.

Rešitev

Kot je navedeno v prejšnjem razdelku, je površina krogle štirikrat večja od površine kroga istega premera, zato bo imel pol -spet premer 30 cm:

30 cm pol -man -Puza: 1413,72 cm² (dvakrat okrožnico istega premera)

Pravokotna pica: (30 cm) x (40 cm) = 1200 cm² .

Semi -Man -pizza ima večje območje.

Reference

1. Fernández J. Številka e. Izvor in radovednosti. Okrevano od: sojina matematika.com
2. Uživajte v matematiki. Eulerjeva številka. Okrevano od: Uživajte.com.
3. Figuera, j. 2000. Matematika 1. Raznovrstno. Co-Bo izdaje.
4. Garcia, m. Številka E v osnovnem izračunu. Okrevano od: matematika.CIENS.UCV.pojdi.
5. Wikipedija. Pi številka. Okreval od: Wikipedia.com
6. Wikipedija. Transcendentne številke. Okreval od: Wikipedia.com