Popolne številke, kako jih prepoznati in primere

A Popolna številka je naravna številka Vsota njegovih delitev je enaka številka. Očitno je ni mogoče vključiti med delitve na številko.

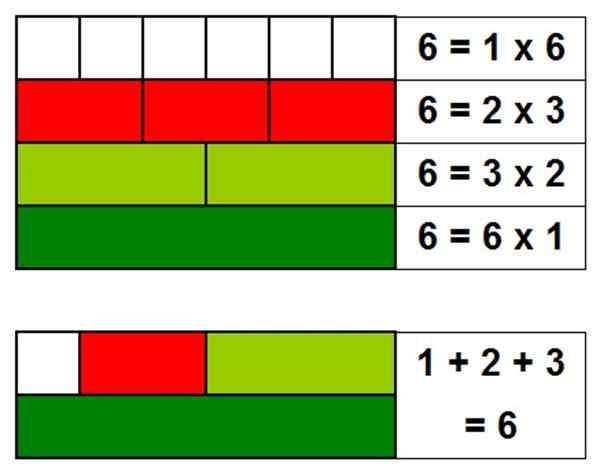
Eden najpreprostejših primerov popolnega števila je 6, saj so njeni delilniki: 1, 2 in 3. Če dodamo delitve, ga dobimo: 1 + 2 + 3 = 6.

Slika 1. Številka 6 je popolna, saj vsota njegovih delitev, ki ne vključuje same številke, daje številko 6. Vir: Self Made

Vsota delilnikov celoštevilca, ki ne vključuje samega števila, se imenuje alikvot. Zato je popolno število enako alikvotu.

Če pa je v vsoto delitev števila vključena samo številka, potem bo popolna številka ena, ki je vsota vseh njegovih delilnikov, deljena s 2.

[TOC]

Zgodovina

Matematiki antike, zlasti Grki, so dali velik pomen popolnim številom in pripisali božanske lastnosti.

Na primer, Philo de Alejandría je približno 1. stoletje trdil, da sta 6 in 28 popolni številki, ki sovpadata s šestimi dnevi ustvarjanja sveta in osemindvajsetimi dnevi, ki jih potrebujejo, da se luna obrne okoli zemlje.

Popolne številke so prisotne tudi v naravi, na primer na severnem polu Saturna se zdi tudi popolna številka 6, vrtinec v obliki šesterokotnika. 

Čebelji satja imajo celice v šesterokotni obliki, torej s 6 straneh.  Pokazalo se je, da je poligon s popolno številko 6 tisti, ki omogoča maksimiranje števila celic v panju čebel, z minimalnim voskom.

Slika 2. Popolna številka 6 je prisotna v čebelah satja. Pokazano je, da je s tem številom strani količina voska, ki se uporablja za oblikovanje celic, minimalna. Vir: Pixabay.

Popolne lastnosti številk

Vsota vseh delilnikov naravnega števila n je označena z σ (n). V popolni številki je res, da: σ (n) = 2n.

Euclid formula in merila

Euclid je odkril formulo in merilo, ki vam omogoča, da najdete popolne številke. Ta formula je:

2^(N-1) (2ⁿ -1)

Vendar bo številka, ki jo ustvari formula, popolna le, če je faktor (2ⁿ -1) Bodite bratranec.

Vam lahko služi: pravokotne sestavine vektorja (z vajami)

Poglejmo, kako nastajajo prve popolne številke:

Če je n = 2, potem imamo 2¹ (2² - 1) = 2 x 3 = 6, da smo že videli, da je popoln.

Ko n = 3 imate 2² (2³ - 1) = 4 x 7 = 28, kar je tudi popolno, kot je podrobno preverjeno v primeru 1.

Poglejmo, kaj se zgodi z n = 4. Z zamenjavo v formuli Euclid imamo:

2³ (2⁴ - 1) = 8 x 15 = 120

Preveriti je mogoče, da ta številka ni popolna, kot je prikazano podrobno v primeru 3. To ne nasprotuje merilom Euclida, saj 15 ni bratranec, kar je nujna zahteva, da je rezultat popolna številka.

Poglejmo, kaj se zgodi, ko n = 5. Uporaba formule, ki jo imamo:

2⁴ (2⁵ - 1) = 16 x 31 = 496

Ker je 31 glavna številka, mora biti številka 496 popolna, glede na merila Euclid. V primeru 4 je podrobno prikazano, da je učinkovito.

Najpomembnejše številke, ki imajo obrazec 2^str - 1 Imenujejo se bratranci Mersenne, v čast menih Marin Mersenne, ki je v sedemnajstem stoletju preučeval glavne številke in popolne številke.

Kasneje je v osemnajstem stoletju Leonhard Euler pokazal, da so vse popolno število, ki ga ustvari evklidna formula.

Do danes je bilo najdeno popoln, ki je čuden.

Največja popolna številka znana

Do trenutnega datuma je znano 51 popolnih številk, vse ustvarjene po merilih formule in euklida. To številko je bila pridobljena, ko so našli Mersennovega bratranca, to je: (2^82589933 - 1).

Popolna številka #51 je (2^82589933) X (2^82589933 - 1) in ima 49724095 Digitos.

Popolna številka je prijatelj sebe

V teoriji številk pravijo, da sta dve številki prijatelji, ko je vsota delitve enega, ki ne vključuje samega števila, enaka drugemu številu in obratno.

Lahko vam služi: linijski in polriverski segment

Bralec lahko preveri, ali je vsota delitve 220, ne vključno z 220, 284. Po drugi strani je vsota 284 delitev, ki ne vključuje 284, enaka 220. Zato sta številka 220 in 284 prijatelji.

S tega vidika je popolna številka sebe.

Primeri popolnih številk

Nato je naštetih prvih osem popolnih številk:

6

28

496

8128

33550336

8589869056

137438691328

2305843008139952128

Vaje

V naslednjih vajah bo treba izračunati delitve številke in nato iz njihovega vsota in preveriti, ali je številka popolna številka ali ne.

Zato bomo pred obravnavo vaj pregledali koncept in pokazali, kako se izračunajo.

Za začetek se morate spomniti, da so številke lahko bratranci (ko jih lahko razdelimo le na natančno s seboj in 1) ali spojinami (ko se lahko razgradijo kot produkt osnovnih številk).

Za sestavljeno številko N imate:

N = aⁿ . b^m. c^str … R^k 

Kjer so a, b, c ... r glavne številke in n, m, p ... k, so eksponenti, ki pripadajo naravnim številkam, ki so lahko vredni od 1 naprej.

Glede na te eksponente obstaja formula, ki ve, koliko delitev ima številka N, čeprav nam ne pove, kaj so to. Naj bo C ta znesek, potem pa:

C = (n +1) (m +1) (p +1) ... (k +1)

Razkroj števila N kot produkt glavnih številk in znanje o tem, koliko delitve, tako bratrancev kot tudi ne -pecincev.

Ko imajo vsi, razen zadnjega, ki ni potrebno v znesku, je mogoče preveriti, ali gre za popolno število ali ne.

- Vaja 1

Preverite, ali je številka 28 popolna.

Rešitev

Prva bo razgradnja številke v svojih glavnih dejavnikih.

28 | 2
14 | 2
07 | 7
01 | 1

Njeni delitve so: 1, 2, 4, 7, 14 in 28. Če na 28 izključimo vsoto delitve, daje:

Vam lahko služi: polovica od 15

1 + 2 + 4 + 7 + 14 = 3 + 4 + 7 + 14 = 7 + 7 + 14 = 14 + 14 = 28

Zato je 28 popolna številka.

Poleg tega je vsota vseh njegovih delitev 28 + 28, tako da pravilo σ (28) = 2 x 28.

- Vaja 2

Odločite se, ali je številka 38 popolna ali ne.

Rešitev

Številka je razdeljena na njegove glavne dejavnike:

39 | 3
13 | 13
01 | 1

Delitve 39, ne da bi sami vključili številko, so: 1, 3 in 13. Vsota 1 + 3 + 13 = 4 + 13 = 17 ni enaka 39, zato je 39 nepopolna ali ne-perfekcijska številka. 

- Vaja 3

Ugotovite, ali je številka 120 popolna ali nepopolna.

Rešitev

Številka je razdeljena na njegove glavne dejavnike:

120 | 2
060 | 2
 30 | 2
 15 | 3
  5 | 5
  1 | 1

Iz glavnih dejavnikov najdemo delitve:

1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 in 120

Če je bilo 120 popolnih, ko dodajate vse svoje delitve, je treba dobiti 2 x 120 = 240. 

1 + 2 + 3 + 4 + 5 + 6 + 8 + 10 + 12 + 15 + 20 + 24 + 30 + 40 + 60 + 120 = 360

Ta rezultat se očitno razlikuje od 240, zato je ugotovljeno, da številka 120 ni popolna številka.

- Vaja 4

Preverite, ali je številka 496, pridobljena z merili Euclid, odlično število.

Rešitev

Številka 496 je razdeljena na njegove glavne dejavnike:

496 | 2
248 | 2
124 | 2
062 | 2
031 | 31
001 | 1

Potem so njihovi delilniki:

1, 2, 4, 8, 16, 31, 62, 124, 248, 496

Zdaj so dodani vsi, razen 496:

1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496

Potrditev, da je res popolna številka.

Reference

1. Baldor, a. 1986. Aritmetika. Codex izdaje in distribucije.
2. Vse o vrhunskih številkah. Številke prijateljev. Okrevano od: medicinska sestra.org.
3. Wolfram Mathworld. Eulerjevo pravilo. Okreval od: Mathworld.Wolfram.com.
4. Wolfram Mathworld. Popolna številka. Okreval od: Mathworld.Wolfram.com.
5. Wikipedija. Popolne številke. Pridobljeno iz: v.Wikipedija.org.
6. Wikipedija. Številke prijateljev. Okrevano od: je.Wikipedija.org.