Koti v vrstah oboda, lastnosti, rešenih vaj

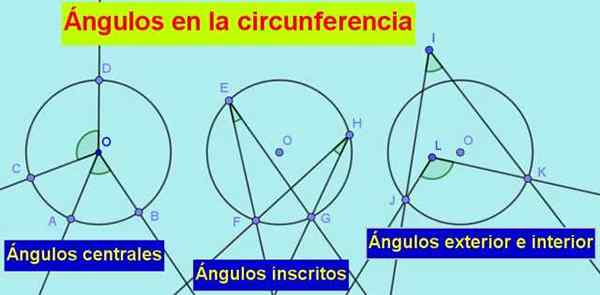
Poklical Koti oboda tistim, v katerih je kateri koli od njegovih elementov ali seka v določenem obodu. Med njimi so naslednje:

1.- On osrednji kot, katere vrhove je v središču oboda in njene strani se sušijo, kot vidimo na naslednji sliki:

Slika 1. Vrste kotov v obodu so: osrednja, vpisana, zunanjost in notranjost. Vir: f. Zapata.

2.- On registrirani kot, katerih točka je na obodu in njene strani so suhe ali tangentne do oboda.

3.- Zunanji kot, katerih točka je zunaj oboda, vendar so njene strani suhe ali tangentne do oboda.

4.- On Notranji kot, z vrhom znotraj oboda in njegovimi suhimi stranicami.

Vsi ti koti ohranjajo določene odnose med seboj in to nas vodi do pomembnih lastnosti med koti, ki pripadajo določenemu obodu.

[TOC]

Lastnosti

- Osrednji kot

Osrednji kot je opredeljen kot tisti, katerega točka je v središču oboda, in njene strani so zarežene v obod.

Merilo radianov osrednjega kota je količnik med lokom, ki podreja obod oboda med stranicami kota in polmerom oboda. 

Če je obod enoten, to je polmer 1, potem je merilo osrednjega kota dolžina loka, ki ustreza številu radianov.

Če želite merilo osrednjega kota v stopinjah, se ukrep pomnoži v radianih po faktorju 180 °/π.

Merilni instrumenti kotov, kot sta transporter in goniometer, vedno uporabljajo osrednji kot in dolžino podrejenega loka.

Vam lahko služi: delni derivati: lastnosti, izračun, vaje

Kalibrirajo se v seksualnih stopinjah, kar pomeni, da kadar koli se meri z njimi, je v zadnjem delu dolžina loka, ki ga podredi osrednji kot.

Lastnina

Ukrep osrednjega kota v radianih je enak dolžini loka, ki jo podtinki ali prestrezki delijo z dolžino polmera.

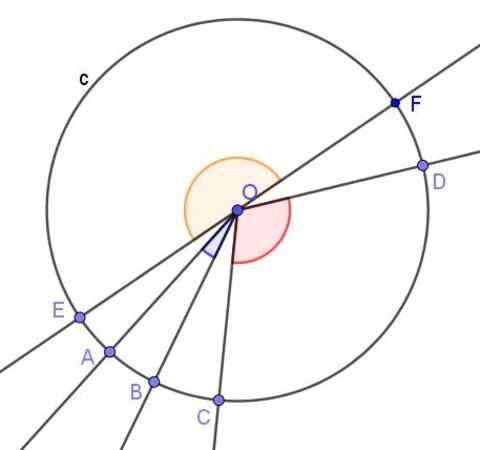Slika 2. Prikazani so trije osrednji koti. En akutni, drugi obljubi in eno stanovanje. Vir: f. Zapata.

- Registrirani kot

Registrirani kot oboda je takšen, ki ima svojo vrhovo na obodu, polta pa je suha ali tangentna. 

Njene lastnosti so:

Lastnosti

-Registrirani kot je izbočen ali raven.

-Ko vpisan kot prestreže isti lok kot osrednji kot, bo mera prvega polovica od drugega.

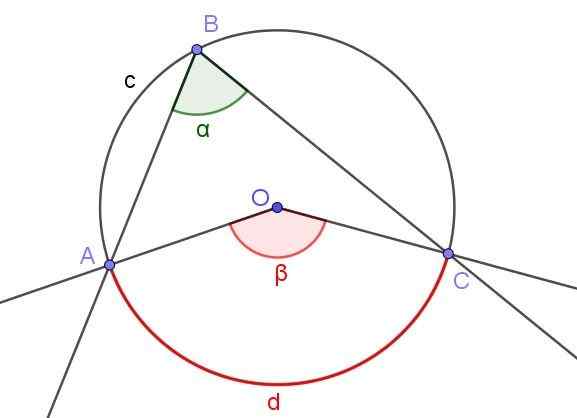Slika 3. Registrirani kot ∠abc in osrednji kot ∠aoc, ki podvije isti lok A⌒c. Vir: f. Zapata.

Slika 3 prikazuje dva kota ∠abc in ∠aoc, ki prestrežeta isti obod A⌒c.

Če je merilo registriranega kota α, je β mera osrednjega kota dvakrat večja mera registriranega kota (β = 2 α), ker oba odštevata isti izmerjeni lok D.

- Zunanji kot

To je kot, katerega točka je zunaj oboda in vsaka njena stran se v eni ali več točkah razreže na obod.

Lastnina

-Njegov ukrep je enak polprešlju (ali razlikam, deljeno z 2) osrednjih kotov, ki sami prestrežejo loke.

Da bi zagotovili, da je ukrep pozitiven, mora biti polkpresi.

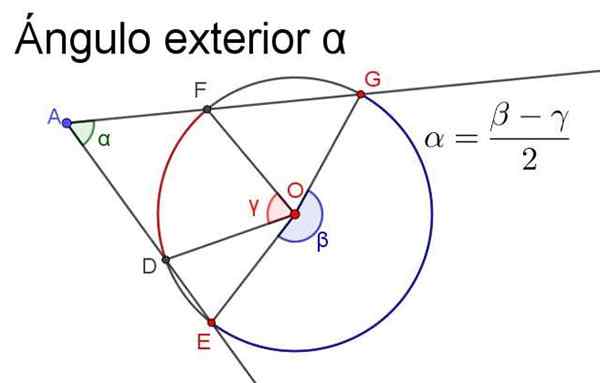Slika 4. Zunanji kot α je enak polreferenci centralov, ki subtizirajo iste loke. Vir: f. Zapata.

- Notranji kot

Notranji kot je tisti, katerega točka je znotraj oboda in njene strani so razrezane na obod.

Vam lahko služi: koeficient določanja: formule, izračun, razlaga, primeri

Lastnina 

Njegov ukrep je enak polseto osrednjega kota, ki podredi isti lok, in osrednji kot, ki podredi isti lok kot njen podaljšek (to je notranji kot, ki ga tvori pol -utrip, ki dopolni do tistih izvirnikov notranji kot).

Naslednja slika prikazuje in razjasni lastnost notranjega kota.

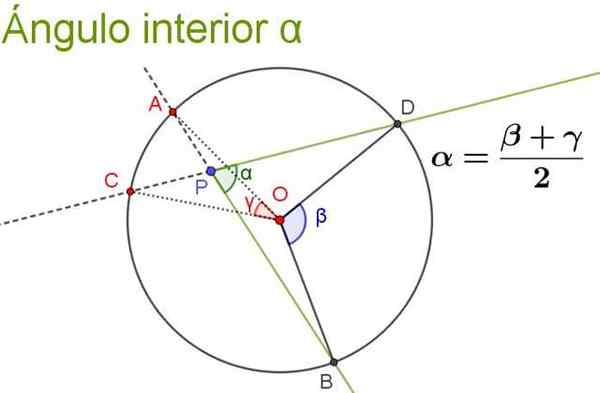Slika 5. Notranji kot α je enak polseizmumu osrednjega kota, ki subtinirajo iste loke kot sam on. Vir: f. Zapata.

Rešene vaje

- Vaja 1

Predpostavimo, da je vpisan kot, v katerem ena od njenih strani gre skozi sredino oboda, kot je prikazano na sliki 6. Polmer oboda je oa = 3 cm in lok d ima dolžino π/2 cm. Določite vrednost α in β kotov.

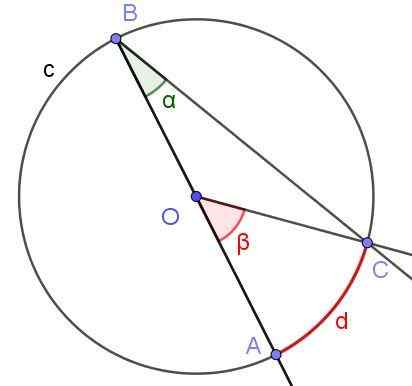Slika 6. Registrirani kot ∠abc s stranjo [BA) skozi O in osrednji kot ∠aoc.Vir: f. Zapata.

Rešitev

V tem primeru se tvori trikotni trikotni cob, saj [oc] = [ob]. V izosceles trikotniku so koti, ki mejijo na podlago, enaki, zato morajo ∠BCO = ∠abc = α. Po drugi strani ∠COB = 180 ° - β. Glede na vsoto notranjih kotov Trikotnika COB imate:

α + α + (180 ° - β) = 180 °

Od kod sledi, da 2 α = β ali kaj je enakovredna α = β/2, kar potrjuje lastnost (3) prejšnjega odseka ista vrv [AC].

Zdaj določamo številčne vrednosti: β kot je osrednji in njegov ukrep v radianih je razmerje med lokom d in polmerom r = oa, zato je njen ukrep:

β = d / r = (π / 2 cm) / (3 cm) = π / 6 rad = 30 °.

Vam lahko služi: štirikolesni: elementi, lastnosti, klasifikacija, primeri

Po drugi strani je bilo že potrjeno, da je α = β / 2 = (π / 6 rad) / 2 = π / 12 rad = 15 °. 

- Vaja 2

Na sliki 7 koti α₁ in β₂ imajo isti ukrep. Poleg tega kot β₁ Meri 60 °. Določite kota β in α.

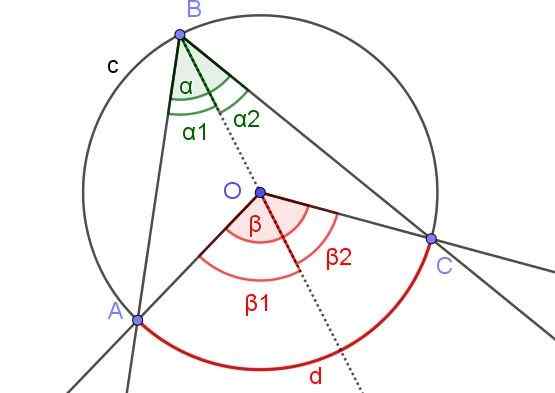Slika 7. Na sliki α₁ = β₂ in β₁ = 60 °. Določite vrednosti β in α. Vir: f. Zapata.

Rešitev

V tem primeru je vpisan kot ∠abc, v katerem je središče ali obod znotraj kota.

Zaradi premoženja (3) imate α₂ = β₂ /2 in α₁ = β₁ /2. Kot:

α = α₁ + α₂ in β = β₁ + β₂

Zato imate:

α = α₁ + α₂ = β₁ /2 + β₂ /2 = (β₁ + β₂) / 2 = β / 2.

To je po lastnostih:

α = β / 2

Kot nam rečejo, da β₁ = 60 ° potem:

α₁ = β₁ / 2 = 60 ° / 2 = 30 °.

Pravijo tudi, da α₁ = β₂ Torej sledi, da:

β₂ = 30 °.

Kot β je:

β₁ + β₂ = 60 ° + 30 ° = 90 °.

In kot α = β / 2, potem:

α = 90 ° / 2 = 45 °. 

V zaključku:

β = 90 ° in α = 45 °.

Reference

1. Baldor, a. 1973. Geometrija in trigonometrija. Srednjeameriški kulturni uvodnik.
2. In. Do. 2003. Elementi geometrije: z vajami in geometrijo kompasa. Univerza v Medellinu.
3. Geometrija 1. mesto. Koti v obodu. Okreval od: edu.Xunta.je.
4. Vsa znanost. Rešene vaje kotov v obodu. Okreval od: Francesfizike.Blogspot.com
5. Wikipedija. Registrirani kot. Okrevano od: je.Wikipedija.com