Registriran kot definicije kroga, teoremi, primeri

On Registriran kot kroga To je tisti, ki ima svojo vrhovo na obodu, polta pa je suha ali tangentna do istega. Posledično bo registrirani kot vedno izbočen ali raven.

Na sliki 1 je zastopanih več kotov, registriranih v njihovih okoliščinah. Kotni ∠edf je registriran tako, da ima svojo vrhovo d na obodu in njegovim dvema polkrengerjem [od) in [df), ki sušita obod. 

Slika 1. Več vpisanih kotov o njihovih okoliščinah. Vir: f. Zapata z geogebro.

Podobno je registriran kot ∠hgi, ker ima svojo vrtoglavo v obodu in suhe strani na isto.

Koti ∠kjr in ∠ust sta tudi registrirani pri obodu. Prva ima eno sekansko stran in drugo tangento, druga pa dve strani tangenta do oboda, ki tvori ravno ravnino ravnine (180 °).

Nekateri avtorji pokličejo pol vpisan kot tistemu, ki ima eno od njegovih strani tangent do oboda, toda v tem članku se mu zdi registriran.

Vsak registrirani kot določa ali podredi lok, povezan z istim. Na primer na sliki 2 registrirani kot ∠abc podredi lok a⌒c dolžine d.

Ista slika prikazuje kot ∠Doe, ki ni registriran v obodu, ker ni imel svojega oboda, ampak v središču ali.

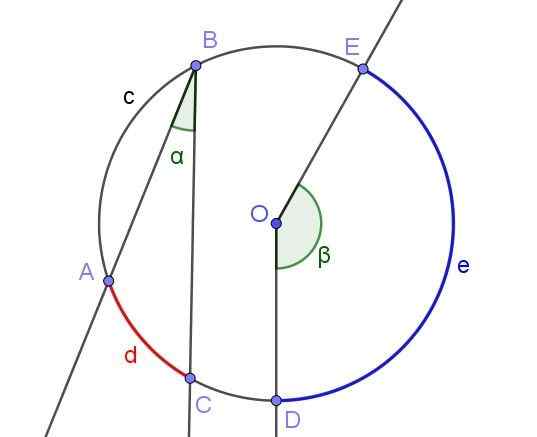Slika 2. Registrirani kot ∠abc in osrednji kot ∠doe. Vir: f. Zapata z geogebro.

[TOC]

Osrednji kot

Poleg registriranega kota osrednji kot, ki je tisti, katerega vrha je v središču oboda in katerih stranice sekajo na obod.

Vam lahko služi: razlika med skupno frakcijo in decimalno številko

Merilo radianov osrednjega kota je količnik med lokom, ki podreja obod oboda med stranicami kota in polmerom oboda.

Če je obod enoten (polmer 1), potem je dolžina loka v istih radijskih enotah merilo kot v radianih.

In ko je merilo kota potrebno v stopinjah, se ukrep pomnoži v radianih s faktorjem 180 °/π.

Merilni instrumenti kotov vedno uporabljajo osrednji kot in dolžino loka, ki ga ta neposredno kalibrira v stopinjah. To pomeni, da kadar koli se meri kot, v ozadju, kar se meri, dolžina loka, ki jo podredi osrednji kot.

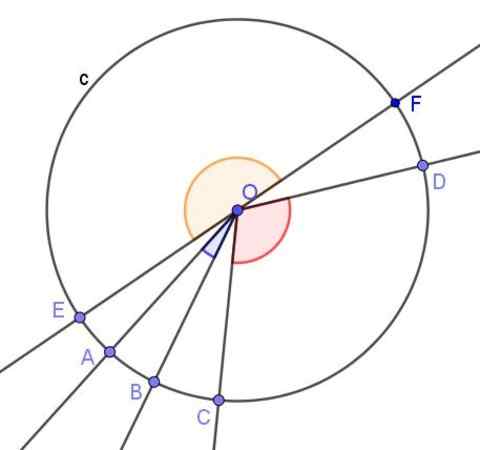Slika 3. Več osrednjih kotov oboda. Vir: f. Zapata z geogebro.

Teoreme

- Teorem 1 (registrirani kot in osrednji kot)

Ukrep registriranega kota je polovica mera osrednjega kota, če oba kota podcenimo isti lok.

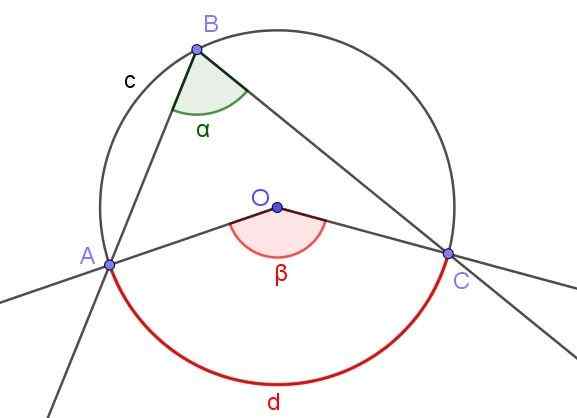Slika 4. Registrirani kot ∠abc in osrednji kot ∠aoc, ki podvije isti lok A⌒c. Vir: f. Zapata z geogebro.

Slika 4 prikazuje dva kota ∠abc in ∠aoc, ki sekata isti obod A⌒c.

Če je merilo registriranega kota α, je β mera osrednjega kota dvakrat večja mera registriranega kota (β = 2 α), ker oba odštevata isti izmerjeni lok D.

Demonstracija 1

Za prikaz teorema 1 se bo začelo več posebnih primerov, dokler ne dosežete splošnega primera.

Vam lahko služi: Zakon o sendvič: Pojasnilo in vaje

Recimo registriran kot, pri katerem ena od njenih strani gre skozi sredino oboda, kot je prikazano na sliki 5.

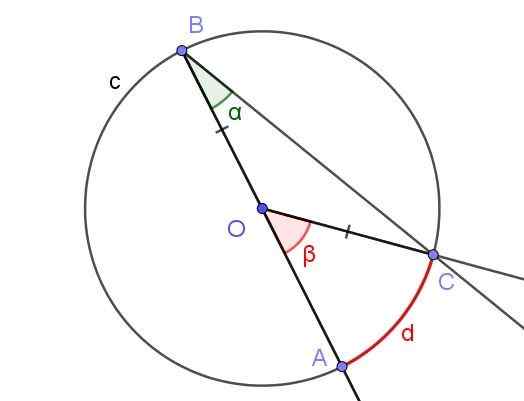Slika 5. Registrirani kot ∠abc s stranjo [BA) skozi O in osrednji kot ∠aoc. Vir: f. Zapata z geogebro.

V tem primeru se tvori trikotni trikotni cob, saj [oc] = [ob].

V trikotniku izosceles so koti, ki mejijo na podlago, enaki, zato morajo ∠bco = ∠abc = α. Po drugi strani ∠COB = 180 ° - β.

Glede na vsoto notranjih kotov Trikotnika COB imate:

α + α + (180 ° - β) = 180 °

Kjer sledi, da je 2 α = β ali kaj je enakovredno: α = β/2. To sovpada s tem, kar navaja teorem 1: Ukrep registriranega kota je polovica osrednjega kota, če oba kota predložita isto vrv [AC].

Demonstracija 1b

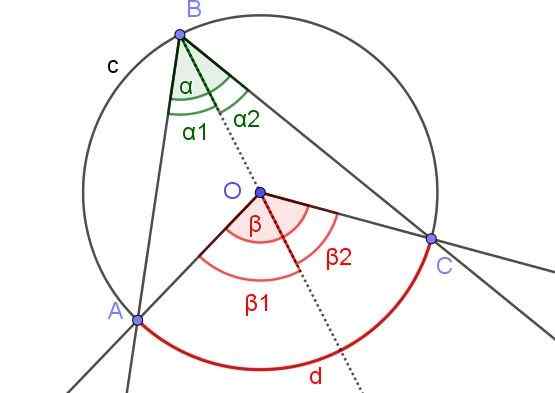Slika 6. Pomožna konstrukcija, da dokaže, da je α = β/2. Vir: f. Zapata z geogebro.

V tem primeru je vpisan kot ∠abc, v katerem je središče ali obod znotraj kota.

Če želite dokazati teorem 1 v tem primeru, je narisan polsredni pomožni [BO), tako da sta dva registrirana kota ∠abo in ∠obc, ki meji.

Podobno imajo osrednje kote β₁ in β₂ v bližini omenjenega polrearevalnega. Na ta način imate enako situacijo kot v demonstraciji 1, zato je mogoče navesti, da α₂ = β₂ /2 in α₁ = β₁ /2. Kot α = α₁ + α₂ in β = β₁ + β₂ Zato obstaja α = α₁ + α₂ = β₁ /2 + β₂ /2 = (β₁ + β₂) / 2 = β / 2.

Vam lahko služi: vrste integralov

Za zaključek α = β / 2, ki ustreza teoremu 1.

- Teorem 2

Če dva ali več registriranih kotov subtsenirata isti lok, potem imata enak ukrep.

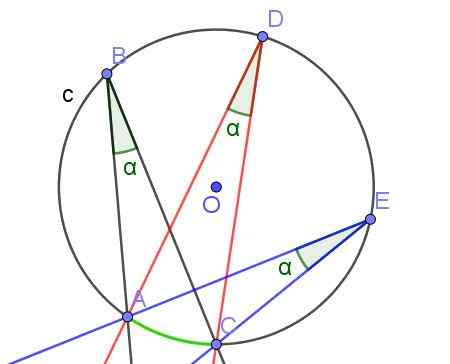Slika 7. Registrirani koti enakega merila α, ker podvržejo istemu loku A⌒c. Vir: f. Zapata z geogebro.

- Teorem 3

Registrirani koti Podvidni so nizi istega ukrepa.

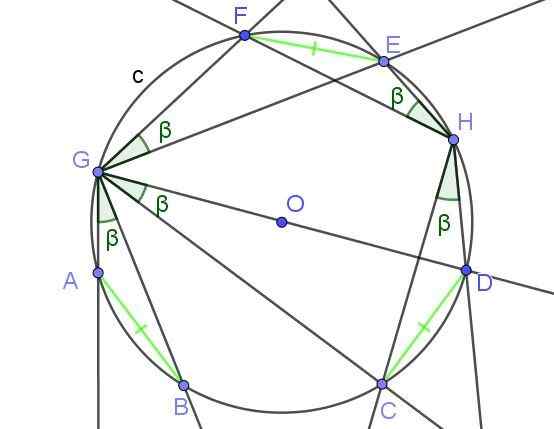Slika 8. Vpisani koti, ki podvržejo vrvi enakega merila, imajo enakega merila β. Vir: f. Zapata z geogebro.

Primeri

- Primer 1

Dokažite, da je vpisan kot podtite premer pravi kot.

Rešitev

Osrednji kot ∠AOB, povezan s premerom, je raven kot, katerega ukrep je 180 °.

V skladu s teoremom 1 ima vsak kot, registriran v obodu, ki podredi isto vrv (v tem primeru premer), kot meri kot polovico osrednjega kota, ki podvije isto vrv, kar je za naš primer 180 °/2 = 90 °.

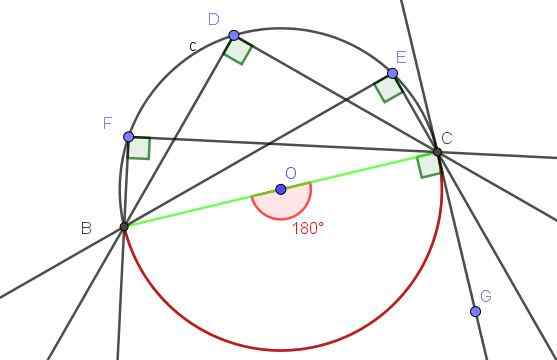Slika 9. Vsak registrirani kot, ki se podredi premeru, je pravi kot. Vir: f. Zapata z geogebro.

- Primer 2

Tangenta črte (BC) v A A A do Oboža C določa vpisan kot ∠Bac (glej sliko 10).

Preverite, ali je teorem 1 registriranega kota izpolnjen.

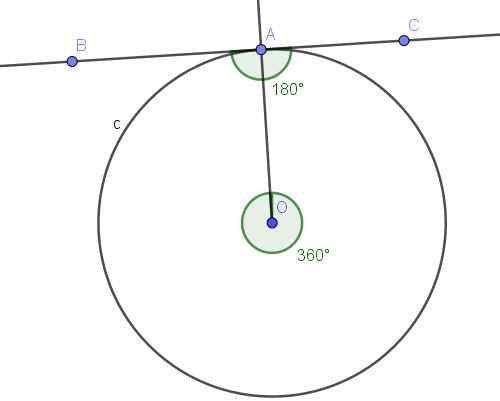Slika 10. Registrirani kot BAC in njegov konveksni osrednji kot AOA. Vir: f. Zapata z geogebro.

Rešitev

Kota ∠Bac je registriran, ker je njena vrha na obodu, stranice [AB) in [AC).

Po drugi strani pa vpisani kot ∠BAC podredi lok A⌒A, ki je popoln obseg. Osrednji kot, ki podredi lok A⌒A, je konveksni kot, katerega ukrep je celoten kot (360 °).

Registrirani kot Podvitek celoten lok meri polovico povezanega osrednjega kota, torej ∠Bac = 360 °/2 = 180 °.

Z vsem zgoraj navedenim je dokazano, da ta primer ustreza teoremu 1.

Reference

1. Baldor. (1973). Geometrija in trigonometrija. Srednjeameriški kulturni uvodnik.
2. In. Do. (2003). Elementi geometrije: z vajami in geometrijo kompasa. Univerza v Medellinu.
3. Geometrija 1. mesto. Koti v obodu. Okreval od: edu.Xunta.je/
4. Vsa znanost. Predlagane vaje kotov v obodu. Okreval od: Francesfizike.Blogspot.com
5. Wikipedija. Registrirani kot. Okrevano od: je.Wikipedija.com