Enakomerno pospešene lastnosti pravokotnega gibanja, formule

On enakomerno pospešeno pravokotno gibanje To je tisti, ki prehaja čez ravno črto in v kateri mobilni telefon s konstantno hitrostjo poveča ali zmanjšuje svojo hitrost. Ta hitrost je velikost, ki opisuje ritem, s katerim se spreminja hitrost in se imenuje pospešek.

V primeru enakomerno pospešenega ali raznolikega pravokotnega gibanja (MRUV) je konstanten pospešek odgovoren za spreminjanje velikosti hitrosti. V drugih vrstah gibanja lahko pospeševanje spremeni tudi smer in občutek hitrosti ali celo spremeniti smer, kot v enotnem krožnem gibanju.

Slika 1. Pospešeni gibi so najpogostejši. Vir: Pixabay.

Ker pospešek predstavlja spremembo hitrosti sčasoma, so njegove enote v mednarodnem sistemu m/s² (metri na nekaj sekundah). Tako kot hitrost lahko tudi pospeševanje dodeli pozitiven ali negativen znak, saj se hitrost povečuje ali zmanjšuje.

Pospeševalna beseda +3 m/s² To pomeni, da se za vsako sekundo, ki mine, mobilna hitrost poveča za 3 m/s. Če je bila na začetku gibanja (pri t = 0) mobilna hitrost +1 m/s, potem bo po sekundi 4 m/s in po 2 sekundah bo 7 m/s.

V enakomerno raznolikem pravokotnem gibanju se spreminjajo hitrosti, ki jih mobilni predmeti vsakodnevno upoštevajo. Je bolj realističen model kot enotno pravokotno gibanje. Še vedno je precej omejen, saj mobilni telefon omejuje, da potuje le na ravni črti.

[TOC]

Značilnosti

To so glavne značilnosti enakomerno pospešenega pravokotnega gibanja:

-Gibanje vedno prehaja po ravni črti.

-Pospešek mobilnega telefona je konstanten, tako v velikosti kot v smeri in pomenu.

-Mobilna hitrost se poveča (ali zmanjšuje) linearno.

-Od pospeška do ostaja konstanten sčasoma t, Graf njene velikosti kot funkcije časa je ravna črta. V primeru, prikazanem na sliki 2, je črta modra in vrednost pospeška se bere na navpični osi, približno +0.68 m/s².

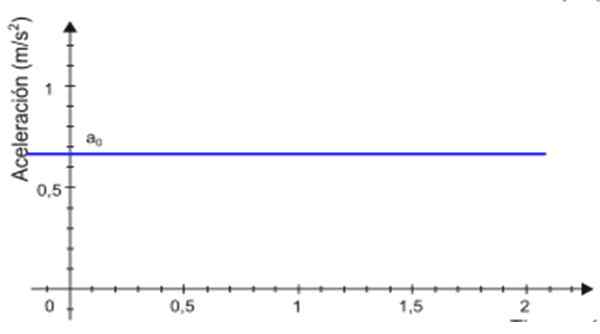Slika 2. Graf pospeška glede na čas za enakomerno raznoliko pravokotno gibanje. Vir: Wikimedia Commons.

-Hitrostni grafikon v približno t To je ravna črta (v zeleni sliki 3), katere naklon je enakovreden mobilnemu pospeševanju. V primeru je naklon pozitiven.

Lahko vam služi: bonski nitrid (BN): struktura, lastnosti, pridobivanje, uporabe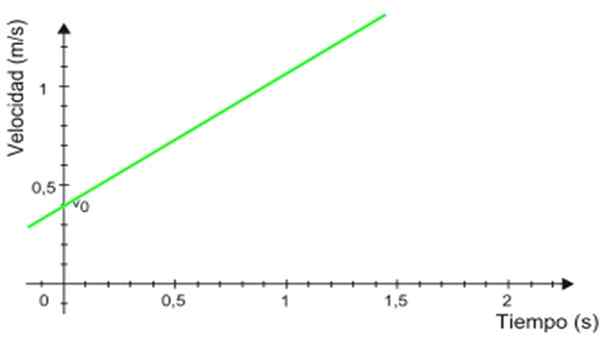 Slika 3. Hitrostni graf, ki temelji na času za enakomerno raznoliko pravokotno gibanje. Vir: Wikimedia Commons.

-Rez z navpično osi označuje začetno hitrost, v tem primeru je 0.4 m/s.

-Končno je graf položaja x v primerjavi s časom krivulja, prikazana na rdeči barvi na sliki 4, ki je vedno prispodoba.

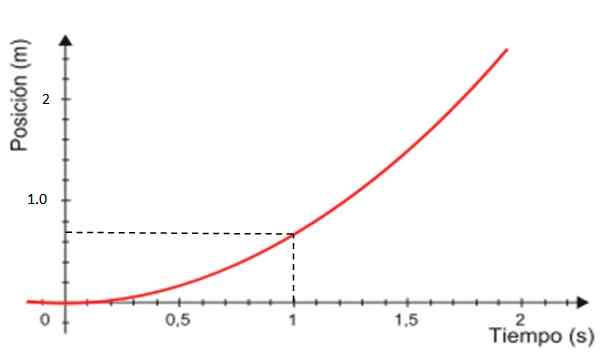Slika 4. Grafika položaja, ki temelji na času za enakomerno raznoliko pravokotno gibanje. Vir: Modified Wikimedia Commons.

Razdalja, prevožena od grafa V proti. t

Z grafom vs. t, izračun razdalje, ki jo prevozi mobilni telefon, je zelo enostaven. Prevožena razdalja je enakovredna območju pod črto, ki je vključena v želeni časovni interval.

V prikazanem primeru predpostavimo, da želite vedeti razdaljo, ki jo prevozi mobilni telefon med 0 in 1 sekundo. Z uporabo tega grafa glejte sliko 5.

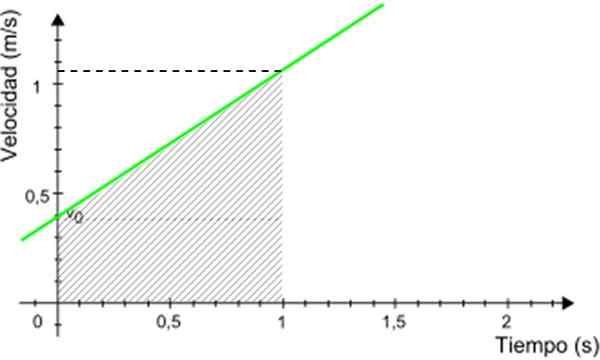Slika 5. Graf za izračun razdalje, ki jo prevozi mobilni telefon. Vir: Modified Wikimedia Commons.

Razdalja je iskala številčno enakovredno območju zasenčenega trapezoida na sliki 3. Trapezoidno območje daje: (Glavna baza + manjša baza) x višina/2

Razdalja prevožena = (0.4 + 1.05) x 1/2 m = 0.725 m

Možno je tudi razdeliti senčeno območje na trikotnik in pravokotnik, izračunati ustrezna območja in jih dodati. Prevožena razdalja je pozitivna, tudi če delček gre v desno ali na levo.

Formule in enačbe

Tako povprečni pospešek in takojšen pospešek imata enako vrednost v MRUV, zato:

-Pospešek: do = konstanta

Kadar je pospešek enak 0, je gibanje enakomerno rektno, saj bi bila hitrost v tem primeru konstantna. Znak do Lahko je pozitiven ali negativen.

Ker je pospešek naklon črte V proti t, je enačba V (t):

-Hitrost, odvisno od časa: v (t) = v_tudi + Ob

Kje v_tudi To je začetna vrednost mobilne hitrosti

-Položaj, odvisno od časa: x (t) = x_tudi + v_tudi T +½at² 

Ko čas ni na voljo, vendar namesto tega obstajajo hitrosti in premiki, obstaja zelo uporabna enačba, ki jo dobimo s čiščenjem časa v (t) = v_tudi + Ob in ga zamenjava v zadnji enačbi. Je približno:

Vam lahko služi: potencialna energija: značilnosti, vrste, izračun in primeri

-Enačba, ki ne vsebuje časa: v² = v_tudi² +2.do.Δx

Rešene vaje

Pri reševanju kinematične vaje je pomembno zagotoviti, da se predlagana situacija prilagodi modelu, ki ga je treba uporabiti. Na primer, enačbe enotnega pravokotnega gibanja niso veljavne za pospešeno gibanje.

In tisti iz pospešenega gibanja niso veljavni za krožno ali ukrivljeno gibanje, na primer. Prva od teh rešenih vaj združuje dve mobilnici z različnimi gibi. Če želite to pravilno rešiti, je treba iti na ustrezen model gibanja.

-Vaja rešena 1

Če želite izvedeti globino vodnjaka, otrok spusti kovanec in hkrati aktivira svojo štoparico, ki se natančno ustavi pri poslušanju valutnega državnega udara proti vodi. Njegovo branje je bilo 2.5 sekund. Če veste, da je hitrost zvoka v zraku 340 m/s, izračunajte globino vodnjaka.

Rešitev

Biti h Globina vodnjaka. Valuta potuje to razdaljo v prostem padcu, enakomerno raznoliki navpični gibanje, z začetno hitrostjo 0, saj se valuta spusti, in stalen pospešek navzdol, enako kot 9.8 m/s². Vzemite si čas t_m Pri tem.

Ko valuta trči v vodo, zvok, ki ga povzroči klik, potuje do otrokovega ušesa, ki ob poslušanju ustavi štoparico. Ni razlogov, da bi verjeli, da se hitrost zvoka med plezanjem po vodnjaku spreminja, zato je gibanje zvoka enakomerno pravokotno. Zvok traja čas t_s Da bi dosegli otroka.

Enačba gibanja za valuto:

H = ½.g.t_m ² = 4.9 T_m ²

Kjer so bili zamenjani x in do enačbe za položaj v prejšnjem razdelku h in g.

Enačba zvočnega gibanja:

h = v_s . t_s = 340 t_s

To je znana enačba Razdalja = hitrost x čas. S tema dvema enačbama obstajajo tri neznanke: H, TM in TS. Za čas obstaja odnos, znano je, da vse traja 2.5 sekund v tem, da se zgodi:

t_m + t_s = 2.5 s

Izenačenje obeh enačb:

4.9 T_m ² = 340 t_s

Čiščenje enega od časa in zamenjavo:

4.9 T_m ²= 340.(2.5 - t_m)

Pri razvoju izraza pravi in ​​prenosnih izrazov je pridobljen:

Vam lahko služi: navpični posnetek: formule, enačbe, primeri

4.9 T_m ²+340 t_m - 850 = 0

To je enačba druge stopnje z dvema rešitev: 2.416 in -71.8. Izbran je pozitivna rešitev, ki je smiselna, saj čas ne more biti negativen in v vsakem primeru mora biti manjši od 2.5 sekund. Za ta čas ga dobimo z zamenjavo globine vodnjaka:

4.9 T_m ²= 4.9 x 2.416² M = 28.6 m

-Vaja Rešena 2

Avto, ki potuje pri 90 km/h, se približa prečni aveniji s semaforjem. Ko je tam 70 m, je vklopljena rumena luč, katere trajanje je 4 sekunde. Razdalja med semaforjem in naslednjim vogalom je 50 m.

Voznik ima te dve možnosti: a) Stojite na - 4 m/s² ali b) pospešite pri + 2 m/s². Katera od obeh možnosti vozniku omogoča, da se ustavi ali prečka celotno pot, preden se svetloba spremeni v rdečo?

Rešitev

Začetni položaj voznika je x = 0 samo, ko zagleda rumeno luč. Pomembno je pravilno pretvoriti enote: 90 km/h je enako 25 m/s.

Glede na možnost a) v 4 sekundah, da rumena luč zdrži voznik:

x (t) = v_tudi T +½at²= 25.4 -½.(-4).4²M = 68 m (2 metra pred semaforjem)

Analiza možnosti b) imate:

x (t) = v_tudi T +½at²= 25.T +½.2.t²

Medtem ko rumena luč traja, voznik potuje na ta način:

x = 25.4 +½.2.4²M = 116 m

Toda 116 m je manjša od razdalje, ki je na voljo za dosego naslednjega vogala, ki je 70 + 50 m = 120 m, zato ne uspe prečkati celotne ulice, preden se vklopi rdeča luč. Priporočeno je, da se ustavite in ostanete 2 metra od semaforja.

Prijave

Vsak dan ljudje doživljajo učinke pospeška: ko potujejo z avtomobilom ali avtobusom, saj se morajo nenehno ustaviti in pospešiti, da pohod prilagodijo oviram ceste. Pospešek se doživi tudi, ko gre v dvigalo navzgor ali navzdol.

Zabavni parki so mesta, kjer ljudje plačujejo, da doživijo učinke pospeška in se zabavajo.

V naravi se enakomerno raznoliki pravokotni gibanje opazi, ko predmet prosto spusti ali ko ga vržemo navpično navzgor in se pričakuje, da se bo vrnil na tla. Če je zračna odpornost zaničevana, je vrednost pospeška v gravitaciji: 9.8 m/s2.

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill.40-45.
2. Figueroa, d. Fizične serije za znanost in inženiring. Zvezek 3. Izdaja. Kinematika. 69-85.
3. Giancoli, d.  Fizika: načela z aplikacijami. 6^th. Ed Prentice Hall. 19-36.
4. Hewitt, Paul. 2012. Konceptualna fizikalna znanost. 5^th. Ed. Pearson. 14-18.
5. Kirkpatrick, l. 2007. Fizika: pogled na svet. 6^ta Skrajšana izdaja. Cengage učenje. 15-19.
6. Wilson, J. 2011. Fizika 10. Pearson Education. 116-119